数值计算(六)——函数逼近 (2)正交多项式多项式和最小二乘法

正交多项式

上一节中我们学会了最佳一致逼近和平方逼近的方式求解函数逼近多项式，但是发现在求解法方程时，多元方程求解难度较大，如果我们能够将对应的法方法的矩阵直接变为只有对角线元素不为零的矩阵，将极大降低计算的运算量，因此我们引入了正交函数族的概念，从而得出正交多项式。下面简单介绍两种正交多项式勒让德多项式和切比雪夫多项式,其他的正交多项式如：
$Laguerre多项式$，$Hermite多项式$有兴趣的可以自行了解。

勒让德多项式(Legendre)

勒让德多项式的性质

其中最为重要的就是性质一到三和五，第四条基本上不咋用。然后最重要的表格来了，其实也可以用性质三来推出来：

整个题目来理解一下其中的妙处

性质

切比雪夫多项式(Shebyshev)

和上面学勒让德多项式一样来学习切比雪夫多项式；




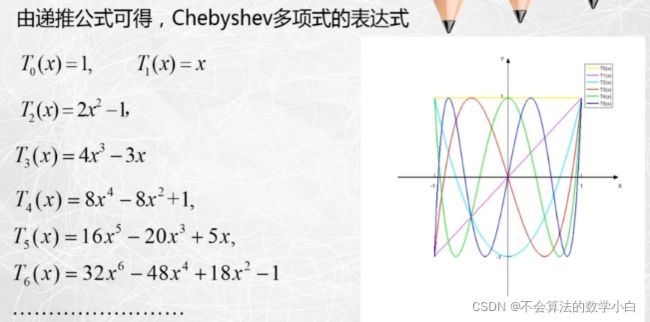
同样的，咱搞个实战试一试

最小二乘法

定义;

求函数$S^{\ast }(x)=\sum _{j=0}^n{\alpha }_j^{\ast }{\phi }_j(x)$的问题可归结为求它的系数${\alpha }_0^{\ast },...,{\alpha }_n^{\ast }$使得多元函数
$F({\alpha }_0,{\alpha }_1,...,{\alpha }_n)\triangleq \sum _{i=1}^m[f(x_i)-\sum _{j=0}^n{\alpha }_j{\phi }_j(x_j){]}^2$取得最小值。由于$F({\alpha }_0,{\alpha }_1,...,{\alpha }_n)$是关于${\alpha }_0,{\alpha }_1,...,{\alpha }_n$的二次函数，所以可以使用多元函数取得极值的必要条件得：
$\frac{\partial F}{\partial {\alpha }_k}=0,(k=0,1,2,...,n)$则通过
$F({\alpha }_0,{\alpha }_1,...,{\alpha }_n)\triangleq \sum _{i=1}^m[f(x_i)-\sum _{j=0}^n{\alpha }_j{\phi }_j(x_j){]}^2$有：
$\frac{\partial F}{\partial {\alpha }_k}=-2\sum _{i=1}^n\{[f(x_i)-\sum _{j=0}^n{\alpha }_j{\phi }_j(x_i)]{\phi }_k(x_i)]\}=0,(k=0\sim n)$
得到方程组：
$\sum _{i=1}^m(\sum _{j=0}^n{\phi }_k(x_i){\phi }_j(x_i)){\alpha }_j=\sum _{i=1}^{m}f(x_i){\phi }_k(x_k)$在离散情况下，$f(x),g(x)$关于点$x_1,x_2,x_3,...,x_m$的内积为$(f,g)=\sum _{i=1}^{m}f(x_i)g(x_i)$也就是说可以将方程组改写为如下形式：$\sum _{j=0}^n({\phi }_k,{\phi }_j){\phi }_j=(f,{\phi }_k),(k=0\sim n)$，再改写为矩阵形式：

也就得到了对应的线性拟合模型。

多项式拟合

在离散数据$(x_i,y_i{)}_{i=1-m}$的最小二乘拟合中，最简单，最常用的数学模型就是多项式，取${\phi }_0(x)=1,{\phi }_1(x)=x,{\phi }_2(x)=x^2,...,{\phi }_n(x)=x^n$得到的拟合函数$f(x)=c_0+c_{1}x+c_2{x}^2+...+c_n{x}^n$
称为多项式拟合。
加权的最小二乘法一般是在通常拟合函数前加一个加权函数乘以拟合部分，具体的可以自己百度一下，嘻嘻。

最小二乘法实战

函数逼近我们将告一段落，后面我们将开启数值积分的版块，船新版本哦，等你来学！！！

欢乐的时光总是短暂的，让我们下一次再见！！！

good good study,day day up! (study hard, improve every day)

预知后事，请听下回分解！！！！