一文带你了解全覆盖路径规划算法(CCPP)

1 前言

全覆盖路径规划(complete coverage path planning, CCPP)问题的任务是确定一条路径，该路径在避开障碍物的情况下通过一个区域或一定空间范围内的所有点。

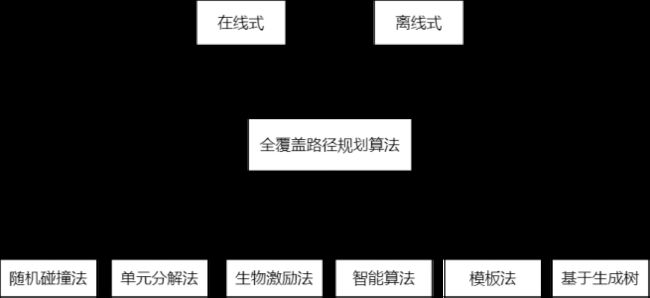
Choset根据环境地图是否先验已知，将全覆盖路径规划算法分为“在线式”和“离线式”两类。离线式CCPP算法只依赖于静态环境信息，并且假设环境是先验已知的。然而，在许多情况下，假设对环境有充分的先验知识可能是不现实的。在线式CCPP算法不假设对要覆盖的环境有充分的先验知识，而是利用传感器数据实时扫描目标空间。因此，这些后期算法也被称为基于传感器的覆盖算法。

根据CCPP算法工作原理不同，可以分为随机碰撞法、单元分解法、生物激励法、模板法、智能算法等，但CCPP算法都应该满足覆盖必须满足的要求，主要有：

1. 机器人必须通过目标区域内除障碍物外的所有点，完全覆盖目标区域；
2. 机器人在覆盖过程中应尽量避免路径重复；
3. 为了控制方便，应尽量使用简单的运动轨迹(例如，直线或圆)；
4. 在允许条件下，获得一条“最优”路径(路线总长度最短或能量消耗最少)；

2 随机碰撞法

随机碰撞法本质上是一种用时间换取空间的算法，它的思路是是机器人选择任意一个初始方向，驱动机器人在环境中直线行走，覆盖这条直线范围中的面积，当机器人检测到障碍物时，使机器人顺时针转过一定角度，并重复上述过程。这种策略的覆盖面积具有极大的随机性，从理论上讲，给定充足的时间，能够使机器人覆盖足够的空间范围，但这种方法非常低效。这种方法的优点是：不需要复杂的定位传感器，通常只需要配备红外传感器，也不需要耗费巨大的计算资源；这种方法的缺点是：在局部范围内存在大量的重复路径，且环境适用性差，当环境中有多个子场景时，特别是两个子场景之间通过狭长的走廊连接，随机碰撞法可能会耗费大量的无用时间才能够从一个区域走到另外一个区域。

在实际使用过程中，扫地机器人常常会因为动态的障碍物等信息陷入困局，调用随机路径覆盖挣脱此困局也是一种常见的手段。

3 单元分解法

单元分解法是将整个空间中的自由区域通过某种方法分割为简单且无重叠区域的子区域，每一部分子区域称为细胞，这些细胞的并集刚好填满整个自由空间，机器人使用简单的覆盖方式(比如往复运动或螺旋运动)对每个子区域进行覆盖，当完成每个子区域的覆盖后，就实现了整个区域的全覆盖。

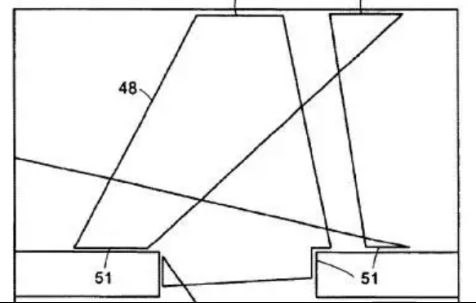
以梯形分解法为例，它是最简单的精确细胞分解方法。该方法先使机器人沿着空间的边缘行走一圈，构建整个区域地图，然后用一条竖直的切割线从左至右扫描过整个区域，党切割线与多边形障碍物的顶点相遇时，就会分解出一个子区域，这样整个自由空间就被分解为诸多子区域，每个子区域都是梯形。机器人在每个子区域中进行往复运动对子区域进行覆盖。梯形分解法如图所示。

其他代表方法有：牛耕单元分解法[1,2]、莫尔斯分解法[3,4]、线扫分割法等。
这里不过多叙述，感兴趣可以阅读参考文献。

4 生物激励法

Yang和Luo将生物激励的神经网络模型应用在清洁机器人的全覆盖路径规划工作上。他们首先对环境进行建模，利用栅格地图对环境进行表示，每一个栅格点对应一个神经元细胞，并提出了分流方程用来计算周围神经元对当前神经元的激励或抑制程度，分流方程如下式所示。

$$\frac{d{x}_i}{dt}=-A{x}_i+\left(B-x_i\right)\left({\left[I_i\right]}^{+}+\underset{j=1}{\stackrel{k}{\Sigma }}{\omega }_{ij}{\left[x_j\right]}^{+}\right)-\left(D+x_i\right){\left[I_i\right]}^{-}$$

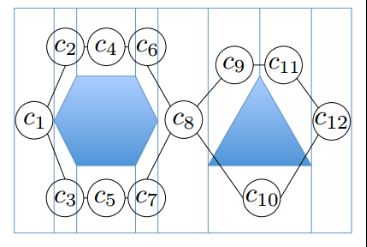
其中xi表示第i个神经元的状态；A是非负常数，表示神经元活性的衰减速率；B、D代表神经元状态的上下限；Ii代表外部输入，ωij表示第i个神经元与第j个神经元的连接权值，一般由两个神经元之间的距离计算得到。第i个神经元的活性值连接图如图所示。

机器人处于某一栅格时，会计算周围神经元的活性值，选择其中活性值最大的栅格作为下一步位置。生物激励法的优点是适用性好，且在避障和实时性方面表现较好，缺点是可能会导致路径重复率较高。

5 模板法

模板法由Neumann de Carvalho R等人提出，依赖于二维环境地图的先验知识，并可以处理地图上没有表示的意外障碍，他们将机器人的运动行为预先规定为七种固定的模板，如下图所示。这些模板包含了机器人在地图中可能遇到的所有情况，机器人根据模板在地图中运动，最终实现地图的全覆盖。

模板法的优点是原理简单，计算消耗小，可以处理动态障碍物；缺点是需要地图的先验知识，适用性较差，智能度较低。

6 智能算法

Wang[5]将遗传算法与牛耕单元分解法结合，当使用分割线将整个自由空间划分为子区域后，通过遗传算法对各子区域进行编码，简历子区域与子区域之间的基点信息，并通过遗传算法得到最优覆盖序列，在每个子区域内以往复运动的形式实现覆盖，将CCPP问题转化为旅行商问题(TSP)。

Zhang[6]将蚁群算法引入单元分解法，根据两个子区域之间的连通性信息定义距离矩阵，并采用蚁群算法根据距离矩阵优化覆盖顺序，他们的实验结果表明，这样结合的算法不仅能保证覆盖所有工作空间，而且规划路径更短，路径重叠率更小，规划效率更高，但对于复杂环境，很难避开障碍物附近的恢复区域。

7 参考文献

[1] Choset, H. Coverage of Known Spaces: The Boustrophedon Cellular Decomposition[J]. Autonomous Robots 9, 247–253 (2000). https://doi.org/10.1023/A:1008958800904

[2] Rekleitis, I., New, A.P., Rankin, E.S. et al. Efficient Boustrophedon Multi-Robot Coverage: an algorithmic approach[J]. Ann Math Artif Intell 52, 109–142 (2008). https://doi.org/10.1007/s10472-009-9120-2

[3] Acar EU, Choset H, Rizzi AA, Atkar PN, Hull D. Morse Decompositions for Coverage Tasks[J]. The International Journal of Robotics Research. 2002;21(4):331-344. doi:10.1177/027836402320556359

[4] Acar EU, Choset H. Sensor-based Coverage of Unknown Environments: Incremental Construction of Morse Decompositions[J]. The International Journal of Robotics Research. 2002;21(4):345-366. doi:10.1177/027836402320556368

[5] Z. Chibin, W. Xingsong and D. Yong, Complete Coverage Path Planning Based on Ant Colony Algorithm[C], 2008 15th International Conference on Mechatronics and Machine Vision in Practice, Auckland, New Zealand, 2008, pp. 357-361, doi: 10.1109/MMVIP.2008.4749559.

[6] Gabriely, Y., Rimon, E. Online Scan Coverage of Grid Environments by a Mobile Robot[J]. In: Boissonnat, JD., Burdick, J., Goldberg, K., Hutchinson, S. (eds) Algorithmic Foundations of Robotics V. 2004. Springer Tracts in Advanced Robotics, vol 7. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-540-45058-0_25