细粒度结构化稀疏神经网络：第二节

摘要

深度神经网络 (DNN) 中的稀疏性已被广泛研究以压缩和加速资源受限环境中的模型。它通常可以分为非结构化细粒度稀疏性（将分布在神经网络中的多个个体权重归零）和结构化粗粒度稀疏性（修剪神经网络的子网络块）。细粒度稀疏可以实现高压缩比，但对硬件不友好，因此速度增益有限。另一方面，粗粒度的稀疏性不能同时在现代 GPU 上实现明显的加速和良好的性能。在本文中，我们第一个研究从头开始训练（N:M）细粒度结构化稀疏网络，该网络可以在专门设计的 GPU 上同时保持非结构化细粒度稀疏性和结构化粗粒度稀疏性的优势。

具体来说，一个（2 : 4）稀疏网络可以在 Nvidia A100 GPU 上实现 2 倍加速而不降低性能。此外，我们提出了一种新颖有效的成分，一种稀疏精炼的直通估计器（SR-STE），以减轻优化过程中由普通 STE 计算的近似梯度的负面影响。我们还定义了一个度量，即稀疏架构发散 (SAD)，以测量训练过程中稀疏网络的拓扑变化。最后，我们用 SAD 证明了 SR-STE 的优势，并通过对各种任务进行综合实验证明了 SR-STE 的有效性。

第二节 简要介绍

深度神经网络 (DNN) 在包括计算机视觉、自然语言处理、语音识别等在内的各种任务上都表现出了可喜的表现。然而，DNN 通常带有大量可学习的参数，范围从数百万到数十亿（例如, GPT-3 (Brown et al., 2020))，使得 DNN 模型繁重且难以应用于实际部署。因此，研究人员开始研究如何通过知识蒸馏 (Hinton et al., 2015)、量化 (Jacob et al., 2018; Zhou et al., 2017)、设计高效模型架构等各种方法来加速和压缩 DNN (Howard et al., 2017) 和结构化稀疏性 (Wen et al., 2016; Li et al., 2016)。

在本文中，我们关注稀疏 DNN 的问题。 DNN 中的稀疏性可分为非结构化稀疏性和结构化稀疏性。非结构化稀疏度在任何位置修剪单个权重，这是细粒度的并且可以实现极高的压缩比（Han et al., 2015; Guo et al., 2016）。然而，非结构化稀疏性难以利用矢量处理架构，这会由于读取的依赖序列而增加延迟（Nvidia，2020）。与非结构化稀疏相比，结构化稀疏对硬件更友好，特别是对于块修剪（Wang et al., 2019）、核形状稀疏性（Tan et al., 2020）或通道和滤波器修剪（Li et al., 2016;温等人，2016）。尽管结构化稀疏可以加速商用硬件上的 DNN，但它比非结构化细粒度稀疏对模型性能的损害更大。

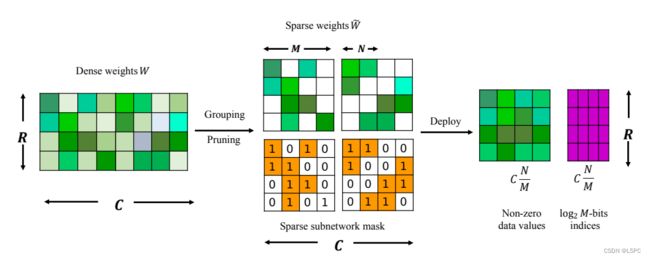
例如，非结构化剪枝生成的 ResNet-50 网络可以达到 5.96 倍的压缩比，与原始网络的精度相同，但在结构化稀疏的情况下只能达到 1 倍的压缩率（Renda et al., 2020 ）。因此，如何结合非结构化稀疏性和结构化稀疏性来加速现代硬件（例如 GPU）上的 DNN 成为一个具有挑战性但有价值的问题。最近，Nvidia Ampere A100 配备了 Sparse Tensor Cores 以加速 2:4 结构化细粒度稀疏性。这里，N:M 稀疏性表示 DNN 的稀疏性，其中对于每个连续的 M 个权重，只有 N 个权重是非零的。据我们所知，A100 是第一个商品稀疏硬件，其中稀疏张量核心可以支持几种常见操作，包括线性、卷积、循环单元、变换器块等。具体来说，假设 DNN 中的典型矩阵乘法 X × W , X 和 W 分别表示输入张量和参数张量。 Dense Tensor Cores 实现 X16×32×W32×8 矩阵乘法 2 个周期，而 Sparse Tensor Cores 只需要 1 个周期，如果参数张量 W 满足 2:4 结构化稀疏模式的话。

Nvidia 提出了一种 ASP1（APEX 的自动稀疏性）解决方案（Nvidia，2020）来稀疏化密集神经网络，以满足 2:4 细粒度结构化稀疏性要求。该配方包含三个步骤：（1）训练密集网络直到收敛； (2) 使用基于幅度的单次剪枝对 2:4 稀疏度进行剪枝； (3) 重复原来的训练过程。然而，ASP 的计算成本很高，因为它需要从头开始训练全密集模型并再次进行微调。因此，我们仍然缺乏一个简单的方法来获得与密集网络一致的结构化稀疏 DNN 模型，而无需额外的微调。

这篇论文解决了这个问题：我们能否设计一个简单而通用的方法来以有效的方式从头开始学习 N:M 稀疏神经网络？在训练稀疏 CNN 和 Transformer 的过程中，很难同时找到最优稀疏架构（连接）和最优参数（Evci 等人，2019b），尽管 SET-MLP 可以轻松胜过密集 MLP（Bourgin 等人，2019）。有两种方案可以获得这样的稀疏模型。一种是两阶段方案，它通过修剪训练有素的密集网络来发现稀疏神经架构，然后使用相同甚至更大的计算资源重新训练稀疏模型（Nvidia，2020；Evci 等人，2019b；Han等人，2015 年；弗兰克和卡宾，2018 年）。另一种是单阶段方案，采用动态方法交替优化参数并根据不同标准修剪网络架构（Bellec et al., 2017; Mocanu et al., 2018; Mostafa & Wang, 2019; Evci et al. .，2019b；Kusupati 等人，2020；Dettmers & Zettlemoyer，2019）。与两阶段方案相比，一阶段方案可以节省训练时间和成本，但通常获得较低的性能。

为了克服上述训练成本和性能之间的权衡，我们提出了一个简单而有效的框架来从头开始训练稀疏神经网络。具体来说，我们在转发过程中采用了基于幅度的剪枝方法（Renda et al., 2020; Gale et al., 2019）。考虑到剪枝操作是不可微的算子（模型量化中的类似困境（Courbariaux 等人，2016）），我们在模型中扩展了广泛使用的直通估计器（STE）（Bengio 等人，2013）量化以帮助稀疏神经网络的反向传播。然而，在反向传播过程中会引入扰动（Yin 等人，2019；Bengio 等人，2013）。因此，我们定义稀疏架构发散（SAD）来进一步分析由 STE 方法训练的 N:M 稀疏网络，以便我们可以识别扰动对稀疏神经网络训练的影响。基于 SAD 分析，为了减轻负面影响，我们提出了一个稀疏细化的术语来减轻近似梯度的影响。

我们还比较了具有不同细粒度结构稀疏度（即 1:4、2:4、2:8、4:8）的神经网络的性能，并对几个具有不同 N 的典型深度神经网络进行了彻底的实验： M个稀疏级别，涵盖图像分类、检测、分割、光流估计和机器翻译。实验结果表明，具有我们提出的结构化稀疏性的模型可以实现可忽略的性能下降，甚至有时甚至可以胜过密集模型。

本文的主要贡献总结为三方面：

(1) 据我们所知，这是第一次系统研究从头开始训练 N:M 结构化稀疏神经网络而没有性能下降。 N:M 结构化稀疏性是模型加速中缺少但有希望的成分，它可以作为各种压缩方法的有价值的补充。

(2) 我们扩展 STE 来解决训练 N:M 稀疏神经网络的问题。为了减轻 STE 在稀疏网络上的局限性，我们提出了一个稀疏细化术语来提高从头开始训练稀疏神经网络的有效性。

(3) 我们对 N:M 细粒度稀疏网络的各种任务进行了广泛的实验，并为 N:M 稀疏网络训练提供基准，以促进相关软硬件设计的共同开发。