【二分】专题练习
题目列表 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
从普及开始。。。。
P8647 [蓝桥杯 2017 省 AB] 分巧克力 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
题目大意:
把n块巧克力分成k块,每块都是正方形,要求边长最大。
这题答案具有单调性,也就是枚举边长时,如果这个边长大了,就往左边找否则在右边找。
因此我们二分边长,如果当前边长能切出的正方形数》=k,则扩大边长,继续搜索。否则减小。
#include
const int N=1e5+10;
long long h[N],w[N];
long long n,k;
bool check(int x)
{
long long res=0;
for(int i=1;i<=n;i++)
{
//int d=std::min(h[i]/x,w[i]/x);
res+=(h[i]/x)*(w[i]/x);
}
return res>=k;
}
signed main()
{
std::cin>>n>>k;
for(int i=1;i<=n;i++) std::cin>>h[i]>>w[i];
int l=1,r=1e5,res=-1;
while(l<=r)
{
int mid=l+r>>1;
if(check(mid))
{
l=mid+1;
res=mid;
}else{
r=mid-1;
}
}
std::cout< P7713 「EZEC-10」打分 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
题目大意:
n个裁判打分,可以把这n个分数加m次1,求去掉最小和最大分后能得到的最大总分。
一开始把题目想简单了,以为简单的贪心就可以,后来发现m》n-2的情况有些复杂。
换个角度思考,总分是确定的即a[1]+a[2]+a[3]+......a[n]+m,我们只要要求最小分和最大分最小就可以了,最小分很显然就是数组中最小的,因为我们不去加他就可以了。剩下的就是要求最大的数字最小,因此想到二分。
我们枚举最大的数字x,如果加m次不能或刚好使所有的数变成x,那么就是满足题意的,我们继续往左边找即可。
#include
const int N=1e5+10;
#define int long long
int a[N];
int n,m,sum;
bool check(int x)
{
int t=0;
for(int i=2;i<=n;i++)
{
t+=x-a[i];
}
return t>=m;
}
signed main()
{
std::cin>>n>>m;
for(int i=1;i<=n;i++)
{
std::cin>>a[i];
sum+=a[i];
}
std::sort(a+1,a+1+n);
int l=a[n],r=2e9,res=-1;
while(l<=r)//要求最大的最小
{
int mid=l+r>>1;
if(check(mid))
{
res=mid;
r=mid-1;
}else l=mid+1;
}
std::cout< B3629 吃冰棍 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
这题通过率低就在于check函数的写法上。
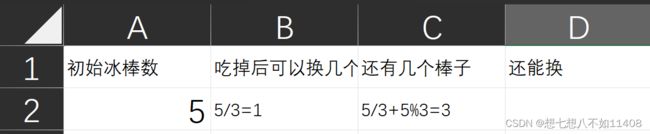
买一根冰棍,吃完了会剩一个木棒;每三个木棒可以兑换一个冰棍。兑换出来的冰棍,吃完之后也能剩下一个木棒。
所以,如果机器猫买了 5 根冰棍,他可以吃完之后得到 5 个木棒;拿 3 个木棒兑换 1 根冰棍,余 2 个木棒;吃完兑换来的冰棍之后,手上有 3 个木棒,又能兑换一个冰棍。最后,机器猫实际上吃了 7 个冰棍。
刚写的时候脑子浆糊了,拉了个excel结果出得很快。
#include
const int N=1e6+10;
int n;
int cal(int x)//冰棒数
{
if(x<3) return 0;
else return cal(x/3+x%3)+x/3;
}
bool check(int x)
{
return cal(x)+x>=n;
}
signed main()
{
std::ios::sync_with_stdio(false),std::cin.tie(0),std::cout.tie(0);
std::cin>>n;
int l=0,r=1e9,res=-1;
while(l<=r)
{
int mid=l+r>>1;
if(check(mid))
{
r=mid-1;
res=mid;
}else l=mid+1;
}
std::cout< P1258 小车问题 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
数学方法
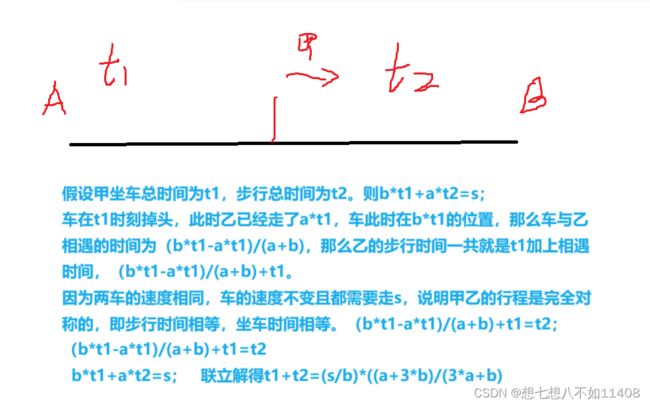
对题目进行分析,甲、乙两人同时从 A 地出发要尽快同时赶到 B 地。出发时 A 地有一辆小车,可是这辆小车除了驾驶员外只能带一人。已知甲、乙两人的步行速度一样,且小于车的速度。问:怎样利用小车才能使两人尽快同时到达。
因为车掉头过程中两人都是步行,此时最不划算,但题目要求二人同时到达,车又必须得掉头接人,故而最理想的状态车只掉头一次。甲中途下车,车去接乙,等乙到达时甲也刚好到达。
因此列方程求解即可。
#include
const int N=1e9+10;
double s,a,b;
signed main()
{
std::cin>>s>>a>>b;
printf("%.6f",(s/b)*((a+3*b)/(3*a+b)));
return 0;
} P1824 进击的奶牛 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
从n个数中选c个,要求这c个数中的最小差最大
#include
const int N=1e5+10;
int n,c;
int a[N];
int st[N];
bool check(int x)
{
int cnt=1;
int last=a[1];
for(int i=2;i<=n;i++)
{
if(a[i]-last>=x)
{
cnt++;
last=a[i];
}
}
return cnt>=c;
}
signed main()
{
std::cin>>n>>c;
for(int i=1;i<=n;i++) std::cin>>a[i];
std::sort(a+1,a+1+n);
int l=0,r=a[n],res=-1;
while(l<=r)
{
int mid=l+r>>1;
if(check(mid))
{
res=mid;
l=mid+1;
}else r=mid-1;
}
std::cout<