【AcWing算法基础】第三讲 搜索与图论

一、DFS

1.1 排列数字

是全排列的问题，很经典的dfs题，没什么难度，硬敲就行

#include
using namespace std;

const int N = 10;

int n;
int path[N];
bool st[N];

void dfs(int cnt){
   
    if(cnt==n){
   
        for(int i=0;i<n;i++){
   
            cout<<path[i]<<" ";
        }
        cout<<endl;
        return;
    }
    
    for(int i=1;i<=n;i++){
   
        if(!st[i]){
   
            path[cnt] = i;
            st[i] = true;
            dfs(cnt+1);
            //-------回溯-------（在递归函数之后）
            st[i] = false;
        }
    }
}

int main()
{
   
    cin>>n;
    dfs(0);
}

1.2 n-皇后问题

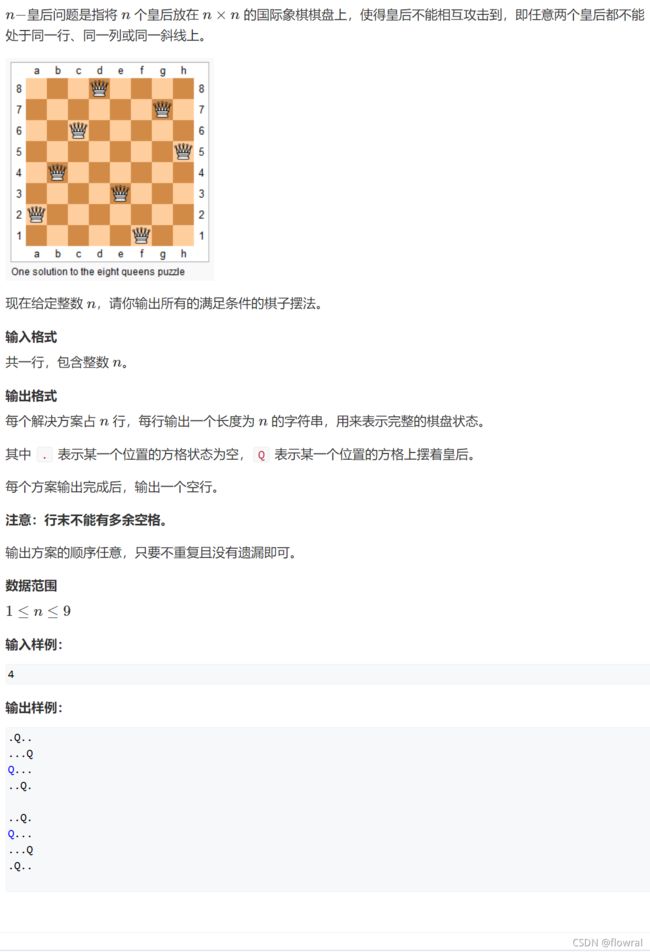
皇后可以上下左右和斜着走
第一种方法和全排列的思想一样，其中对角线的下标需要注意：

对棋盘（矩阵）中的点来说，横纵坐标之和、之差都能确定一条对角线。但因为udg的y-x有可能出现负值（最大为-n）所以映射到数组中，我们需要加上一个n。

#include
using namespace std;

const int N = 20;
char g[N][N];
//col记录的是第i列是否有棋子
//dg记录的是第i个对角线是否有棋子，udg是另一根对角线
bool col[N],dg[N],udg[N];
int n;

void dfs(int cnt){
   
    //cnt既是数量，也是棋盘中的行号
    if(cnt==n){
   
        for(int i=0;i<n;i++){
   
            puts(g[i]);
        }
        puts("");
    }
    
    for(int i=0;i<n;i++){
   
        //这里确保了可行再往下走，所以不会有单独的剪枝
        //
        if(!col[i] && !dg[cnt+i] && !udg[i-cnt+n]){
   
            g[cnt][i] = 'Q';
            col[i] = dg[cnt+i] = udg[i-cnt+n] = true;
            dfs(cnt+1);
            col[i] = dg[cnt+i] = udg[i-cnt+n] = false;
            g[cnt][i] = '.';
        }
    }
}

int main(){
   
    cin>>n;
    
    for(int i=0;i<n;i++)
        for(int j=0;j<n;j++) g[i][j] = '.';
    dfs(0);
}

第二种方法就有点类似于01背包的做法，思路很简单，就是枚举每个格子的两种情况：

#include
using namespace std;

const int N = 20;
char g[N][N];
//col记录的是第i列是否有棋子
//dg记录的是第i个对角线是否有棋子，udg是另一根对角线
bool row[N],col[N],dg[N],udg[N];//因为枚举的是每个格子，所以需要添加行的bool数组
int n;

void dfs(int x,int y,int cnt){
   
    if(y==n) y = 0,x++;
    if(x==n){
   
        if(cnt==n){
   
            for(int i=0;i<n;i++) puts(g[i]);
            puts("");
        }
        return;
    }
    
    //枚举每个棋盘格的两种情况
    if(!row[x] && !col[y] && !dg[x+y] && !udg[y-x+n]){
   
        //放
        g[x][y] = 'Q';
        row[x] = col[y] = dg[x+y] = udg[y-x+n] = true;
        dfs(x,y+1,cnt+1);
        g[x][y] = '.';
        row[x] = col[y] = dg[x+y] = udg[y-x+n] = false;
    }
    
    //不放
    dfs(x,y+1,cnt);
}

int main(){
   
    cin>>n;
    
    for(int i=0;i<n;i++)
        for(int j=0;j<n;j++) g[i][j] = '.';
    dfs(0,0,0);
}

二、BFS

bfs虽然在空间复杂度上不如dfs，但是bfs有个最重要的作用！！那就是搜索最短路！！但是只有等权重相同时才能用来搜索最短路，否则只能使用专门的最短路算法。

2.1 走迷宫

这道题如果只是没有限定最少移动步数，就可以用深搜www（博主太菜了只喜欢写深搜）
这是宽搜的思路：

树的高度就等于从原点到该点的距离
这里多嘴一句，我一开始看到这道题也是想的用dp…但是这道题存在一个环，而**dp是一种没有环的最短路。**所以这道题不能用dp求解。

#include
#include
#include
using namespace std;

typedef pair<int,int> PII;

const int N = 110;
int n,m;
int g[N][N],d[N][N];//d存的是到起点的距离
queue<PII> q;

int bfs(){
   
    q.push({
   0,0});//从起点开始
    
    memset(d,-1,sizeof d);
    d[0][0] = 0;
    
    int dx[4] = {
   -1,0,1,0},dy[4] = {
   0,1,0,-1};
    while(!q.empty()){
   
        auto t = q.front();
        q.pop();//取出队头元素进行计算
        
        //根据取出的这个点，遍历上下左右，符合条件的把它加入队列
        //算是距离相同的点
        for(int i=0;i<4;i++){
   
            int x = t.first+dx[i], y = t.second+dy[i];
            if(x>=0&&y>=0&&x<n&&y<m && g[x][y]==0 && d[x][y]==-1){
   
                //bfs只有第一次搜到的点才为最短距离
                d[x][y] = d[t.first][t.second] + 1;
                q.push({
   x,y});
            }
        }
    }
    
    return d[n-1][m-1];
}

int main()
{
   
    cin>>n>>m;
    for(int i=0;i<n;i++)
        for(int j=0;j<m;j++) cin>>g[i][j];
        
    cout<<bfs();
    
    return 0;
}

如果要记录路径，只用开一个N*N大小的数组，记录一下前一个点。最后从后往前遍历，输出该数组。

2.2 八数码

走迷宫的bfs是：每个状态是一个节点。而八数码的状态则是一串字符串，所以题目不难，思想都是一样的，只是有点绕。

#include
#include
#include
using namespace std;

int bfs(string s){
   
    string end = "12345678x";
    
    queue<string> q;
    unordered_map<string,int> d;
    
    q.push(s);//把最开始的s放进去
    d[s] = 0;//此时的di