软件质量保证与测试 实验一 登录慕测平台Triangle生成相应的JUnit测试用例集
登录慕测平台(http://www.mooctest.net/login2)从慕测开发者测试练习的Triangle程序中选取一条判定语句并依据等价类划分和边界值方法生成相应的JUnit测试用例集
(1)根据所选定的判定语句自行将其中所包含的参数分别划分为2到3个有效等价类
选取了比较简单的if用例
即判断三边是否相等来判断出是否等边三角形
if (triangle.lborderA == triangle.lborderB
&& triangle.lborderB == triangle.lborderC) {
strType = "Regular";
}
假设三边长分别为a、b、c,则可划分四个有效等价类
R1={〈a,b,c〉:有三条边a、b和c的等边三角形}
R2={〈a,b,c〉:有三条边a、b和c的等腰三角形}
R3={〈a,b,c〉:有三条边a、b和c的不等边三角形}
R4={〈a,b,c〉:三条边a、b和c不构成三角形}
根据选定的代码
可以分为等边三角形和非等边三角形两个有效等价类
(2)根据(1)的划分设计满足弱一般等价类的测试用例
| 测试用例 | A | B |C|输出|
| :-----| ----: | :----: |:----: |:----: |:----: |
| test1 | 5| 5 |5|等边三角形
| test2 | 5| 6 |6|非等边三角形
(3)根据(1)的划分设计满足强一般等价类的测试用例
由于A、B、C变量没有有效区间,或者为long的最大值,所以强一般等价类与弱一般等价类测试用例相同.
(4)根据(1)的划分设计满足弱健壮等价类的测试用例
考虑A、B、C无效值产生以下的弱健壮等价类的测试用例
| 测试用例 | A | B |C|输出|
| --| ----| ---- |---- |---- |---- |
| test1 | -1| 5 |5|A不在所能取的范围之内|
| test2 | 5| -1 |6|B不在所能取的范围之内|
| test3| 5| 6 |-1|C不在所能取的范围之内|
| test4 | 1.1| 5 |5|A不在所能取的范围之内|
| test5 | 5| 1.1 |6|B不在所能取的范围之内|
| test6| 5| 6 |1.1|C不在所能取的范围之内|
(5)根据(1)的划分设计满足强健壮等价类的测试用例
| 测试用例 | A | B |C|输出|
| :-----| ----: | :----: |:----: |:----: |:----: |
| test1 | -1| 5 |5|A不在所能取的范围之内
| test2 | 5| -1 |6|B不在所能取的范围之内
| test3| 5| 6 |-1|C不在所能取的范围之内
| test4 | 1.1| -5 |5|A、B不在所能取的范围之内
| test5 | 5| 1.1 |-6|B、C不在所能取的范围之内
| test6| -5| 6 |1.1|A、C不在所能取的范围之内
| test7| -5| 6- |1.1|A、B、C不在所能取的范围之内
(6)设计满足一般边界值的测试用例
一般边界值4n+1
仅考虑有效区间单个变量边界值(一般边界值):用最小值、略高于最小值、正常值、略低于最大值和最大值。以下几处为了方便我们假设最大值为100.
A={1,2,50,99,100}
B={1,2,50,99,100}
C={1,2,50,99,100}
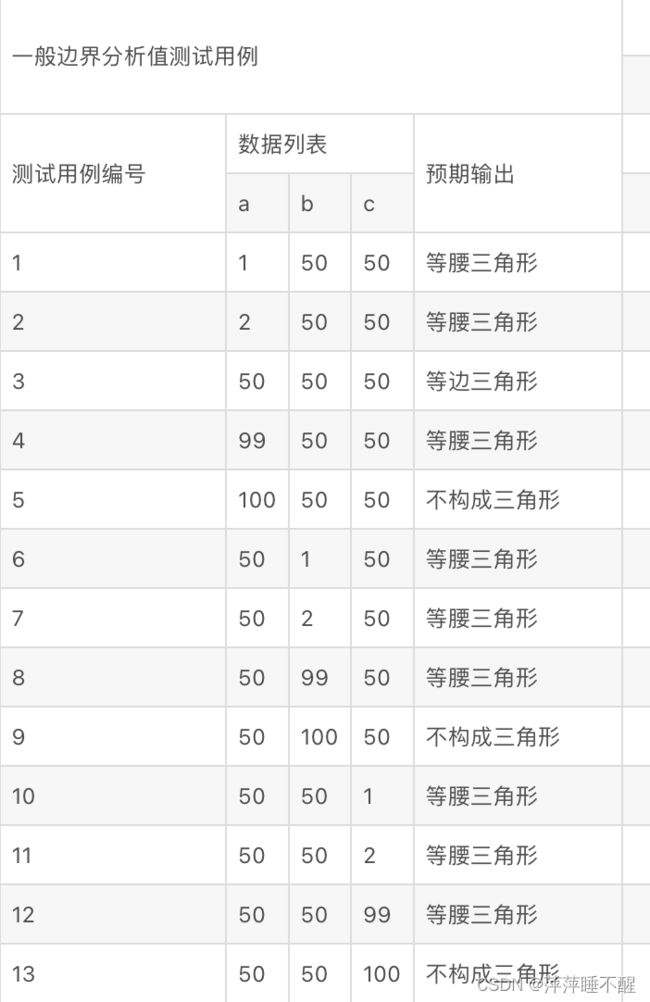
(7)设计满足一般最坏情况边界值的测试用例
最坏情况测试关心的是多变量同时取极值(多缺陷)的情况,首先得到每个变量的min,min+,nom,max-,max(5个),进行笛卡尔乘积。(5^n)个
A={1,2,50,99,100}
B={1,2,50,99,100}
C={1,2,50,99,100}
最坏情况边界值=AXBXC
(8)设计满足健壮边界值的测试用例
健壮边界值6n+1
同时考虑有效区间和无效区间单个变量边界值(健壮边界值):除了最小值、略高于最小值、正常值、略低于最大值、最大值,还要有略超过最大值和略小于最小值的值。
(9)设计满足健壮最坏情况边界值的测试用例
健壮最坏情况测试关心的是多变量同时取极值(多缺陷)的情况,首先得到每个变量的min-,min,min+,nom,max-,max,max+(7个),进行笛卡尔乘积。(7^n)个
A={0,1,2,50,99,100,101}
A={0,1,2,50,99,100,101}
A={0,1,2,50,99,100,101}
健壮最坏情况边界值=AXBXC