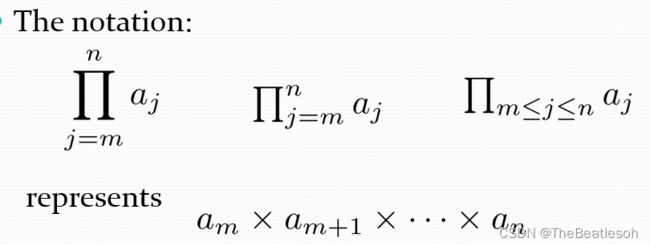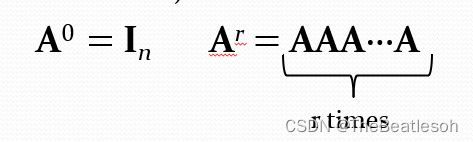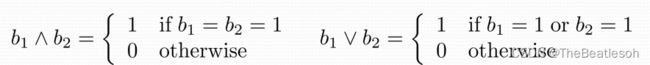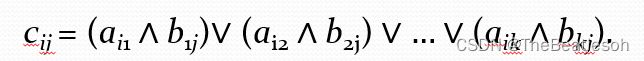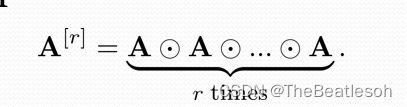离散数学英文名词解释及知识点汇总(第二章)
set 集合
N = natural numbers = {0,1,2,3….}
Z = integers = {…,-3,-2,-1,0,1,2,3,…}
Z⁺ = positive integers = {1,2,3,…..}
R = set of real numbers
R+ = set of positive real numbers
C = set of complex numbers.
Q = set of rational numbers
Universal Set:全集
Empty Set:空集
Subset :子集
Proper Subsets:真子集
Cardinality:基数 The cardinality of a finite set A, denoted by |A|, is the number of (distinct) elements of A.
Power Sets:幂集
Tuple:元组
Truth Sets of Quantifiers:量词的真值集
Boolean Algebra:布尔代数
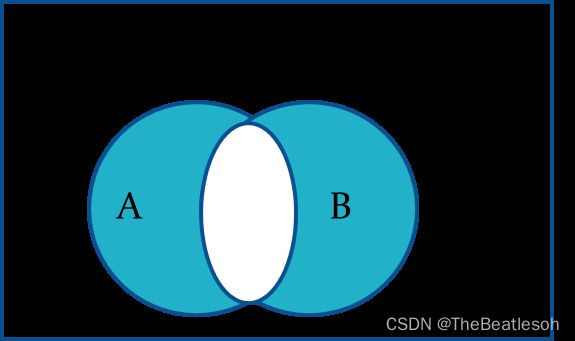
Union:并集
Intersection:交集
Complement:补集
Difference:差集
A – B = {x | x ∈ A Ù x ∉ B} = A ∩`B
Symmetric Difference:对称差集
Set Identities:集合恒等式
Membership Table:成员表
Generalized Unions and Intersections:广义并与交
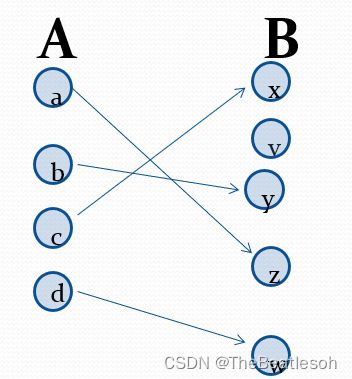
Functions:函数
domain:定义域
codomain:陪域
range:值域
“陪域是输出的可能值的集。陪域是函数定义的一部分。而值域则是输出的实际值的集。”
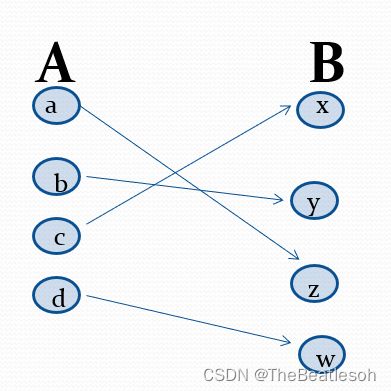
Injections:单射函数 one-to-one or injective
Surjections:满射函数 onto or surjective
Bijections:双射函数 one-to-one correspondence or a bijection
Inverse Functions: 反函数
Graphs of Functions:函数图
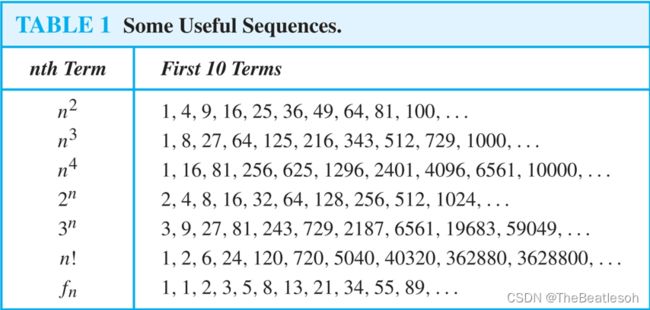
Sequences:序列,数组
Summations:总和
notation:符号,记号
Geometric Progression:等比数列
Arithmetic Progression:等差数列
Strings:字符串
The empty string is represented by λ.
Recurrence Relations:递推关系
equation:方程式
Fibonacci Sequence:斐波那契数列
formula:公式
Product Notation (optional):连乘
Summation Manipulations:求和运算
Geometric Series:几何级数
Cardinality of Sets:集合的基数
Computability:可计算性
Matrices:矩阵(Matrix)
Matrix Multiplication:矩阵乘法
Identity Matrix and Powers of Matrices:单位矩阵与矩阵的幂
Zero-One Matrices:零一矩阵
Boolean Product of Zero-One Matrices:零一矩阵的布尔积
A⊙B
Boolean Powers of Zero-One Matrices :零一矩阵的布尔幂