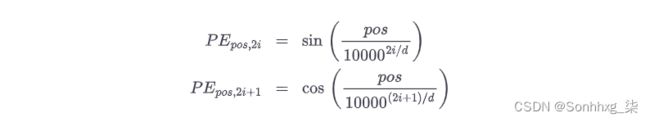【DL】第 7 章 ：用于音乐生成的Transformers和 MuseGAN

除了视觉艺术和创意写作一样，音乐创作是我们认为人类独有的另一种核心创造力行为。

为了让机器创作出悦耳的音乐，它必须克服我们在上一章中看到的与文本相关的许多技术挑战。特别是，我们的模型必须能够学习并重新创建音乐的顺序结构，并且还必须能够从一组离散的可能性中选择后续音符。

然而，音乐生成提出了文本生成不需要的额外挑战，即音高和节奏。音乐通常是复调的——也就是说，不同的乐器同时演奏几条音符流，它们结合起来产生不和谐（冲突）或辅音（和谐）的和声。文本生成只需要我们处理单一的文本流，而不是音乐中出现的平行的和弦流。

此外，文本生成可以一次处理一个词。我们必须仔细考虑这是否是处理音乐数据的合适方法，因为听音乐的大部分兴趣在于合奏中不同节奏之间的相互作用。例如，吉他手可能会弹奏一连串较快的音符，而钢琴家会保持较长的持续和弦。因此，逐个音符生成音乐很复杂，因为我们通常不希望所有乐器同时改变音符。

我们将通过简化问题来开始本章，将重点放在单行（单声道）音乐的音乐生成上。我们将看到，前一章关于文本生成的许多技术也可以用于音乐生成，因为这两个任务有许多共同的主题。特别是，我们将从训练 Transformer 开始，以生成巴赫大提琴组曲风格的音乐，并了解注意力机制如何让模型专注于之前的音符，以确定最自然的后续音符。然后，我们将解决和弦音乐生成的任务，并探索如何部署基于 GAN 的架构来为多种声音创作音乐。

音乐生成Transformer

我们将要构建的模型是一个解码器 Transformer，其灵感来自 OpenAI 的MuseNet ( https://openai.com/blog/musenet/ )，它也使用了一个类似于 GPT-2 的 Transformer。这是一个很好的模型选择，因为音乐乐句的延续通常会受到前几个小节的音符的影响,而不仅仅是前一个音符。例如，以Bach’s Cello Suite No. 1的开头段落为例（图7.1）。

图7.1 Bach’s Cello Suite No. 1（前奏曲）的开场

你认为接下来会出现什么音符？即使您没有受过音乐训练，您仍然可以猜出。如果你说的是 G（与乐曲的第一个音符相同），那么你就是对的。你怎么知道的？您可能已经能够看到每个小节和半小节都以相同的音符开头，并使用此信息来告知您的决定。我们希望我们的模型能够执行相同的技巧——特别是，我们希望它在记录前一个低 G 时注意前一个半小节的特定音符。诸如 Transformer 之类的基于注意力的模型将能够合并这种长期回顾，而不必在许多条形图中保持隐藏状态，循环神经网络就是这种情况。

任何人攻克音乐生成任务首先要对乐理有基本的了解。在下一节中，我们将介绍阅读音乐所需的基本知识，以及我们如何用数字表示这些知识，以便将音乐转换为训练我们的 Transformer 所需的输入数据。书籍存储库中提供了专门用于阅读和解析音乐数据的随附 Jupyter 笔记本。

下载数据

这我们将使用的原始数据集是 JS Bach 大提琴组曲的一组 MIDI 文件。您可以通过运行图书存储库中的数据集下载器脚本来下载数据集，如示例 7-1所示。这会将 MIDI 文件本地保存到/data文件夹中。

示例 7-1 ：下载 JS 巴赫大提琴组曲数据集

bash scripts/download_music_data.sh

到查看和收听模型生成的音乐，您需要一些可以生成乐谱的软件。MuseScore是一个很好的工具，可以免费下载。

解析 MIDI 文件

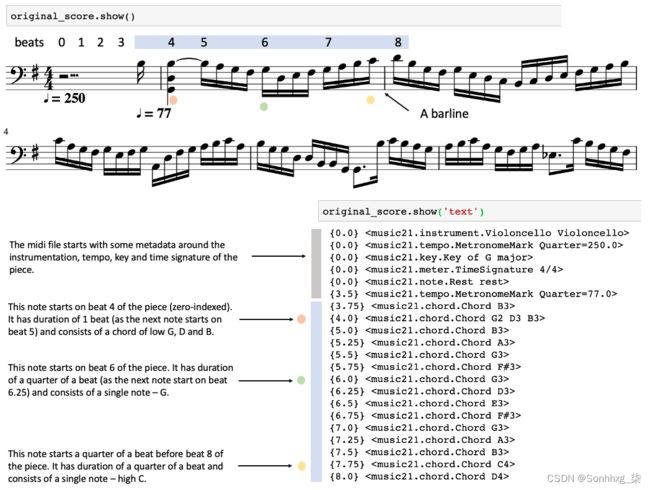
我们会使用 Python 库music21将 MIDI 文件加载到 Python 中进行处理。示例 7-2显示了如何加载 MIDI 文件并将其可视化（图7.2 ），既作为乐谱又作为结构化数据。

示例 7-2 ：导入 MIDI 文件

from music21 import converter

file = "/app/data/bach-cello/cs1-2all.mid"
original_score = converter.parse(file).chordify()

图7.2 乐谱

在第一个示例中，我们将把音乐视为单音（单行），只取任何和弦的最高音符。有时我们可能希望将各个部分分开以生成本质上是复调的音乐。这提出了我们将在本章稍后部分解决的其他挑战。

这示例 7-3中的代码循环遍历乐谱，并将乐曲中每个音符（和休止符）的音高和持续时间提取到两个列表中。每个音符名称后面的数字表示该音符所在的八度音阶——因为音符名称（A 到 G）重复，所以需要用它来唯一标识音符的音高。例如，G2是下面的一个八度G3。此外，我们将乐曲的调号和拍号编码为特殊符号，持续时间为零。

示例 7-3 ：提取数据

notes = []
durations = []

for element in original_score.flat:
    note_name = None
    duration_name  = None

    if isinstance(element, music21.key.Key):
        note_name = str(element.tonic.name) + ':' + str(element.mode)
        duration_name = "0.0"

    elif isinstance(element, music21.meter.TimeSignature):
        note_name = str(element.ratioString) + 'TS'
        duration_name = "0.0"

    elif isinstance(element, music21.chord.Chord):
        note_name = element.pitches[-1].nameWithOctave
        duration_name = str(element.duration.quarterLength)

    elif isinstance(element, music21.note.Rest):
        note_name = str(element.name)
        duration_name = str(element.duration.quarterLength)

    elif isinstance(element, music21.note.Note):
        note_name = str(element.nameWithOctave)
        duration_name = str(element.duration.quarterLength)

    if note_name and duration_name:
        notes.append(note_name)
        durations.append(duration_name)

此过程的输出如表7-1所示。

生成的数据集现在看起来更像我们之前处理过的文本数据。单词是音高-持续时间的组合，我们应该尝试建立一个模型来预测下一个音高和持续时间，给定一系列先前的音高和持续时间。音乐和文本生成之间的一个关键区别是我们需要建立一个模型来同时处理音调和持续时间预测——也就是说，我们需要处理两个信息流，而我们只看到一个文本流在上一章中。

表 7-1 ：每个音符的音高和持续时间，存储为列表

Duration	Pitch
0.0	START
0.0	G:major
0.0	4/4TS
3.75	rest
0.25	B3
1.0	B3
0.25	B3
0.25	A3
0.25	G3
0.25	F#3
0.25	G3
0.25	D3
0.25	E3
0.25	F#3
0.25	G3
0.25	A3

标记化

要创建将训练模型的数据集，我们首先需要标记每个音高和持续时间，就像我们之前对文本语料库中的每个单词所做的一样。我们可以通过使用TextVectorizationLayer, 分别应用于音高和持续时间来实现这一点，如下面的代码块所示。

示例 7-4 ：标记音高和持续时间

def create_dataset(elements):
    ds = tf.data.Dataset.from_tensor_slices(elements).batch(BATCH_SIZE, drop_remainder = True).shuffle(1000)
    vectorize_layer = keras.layers.TextVectorization(standardize = None, output_mode="int")
    vectorize_layer.adapt(ds)
    vocab = vectorize_layer.get_vocabulary()
    return ds, vectorize_layer, vocab

notes_seq_ds, notes_vectorize_layer, notes_vocab = create_dataset(notes)
durations_seq_ds, durations_vectorize_layer, durations_vocab = create_dataset(durations)
seq_ds = tf.data.Dataset.zip((notes_seq_ds, durations_seq_ds))

完整的解析和标记化过程如图 7.3 所示。

图 7.3 解析 MIDI 文件并对音高和持续时间进行标记

创建训练集

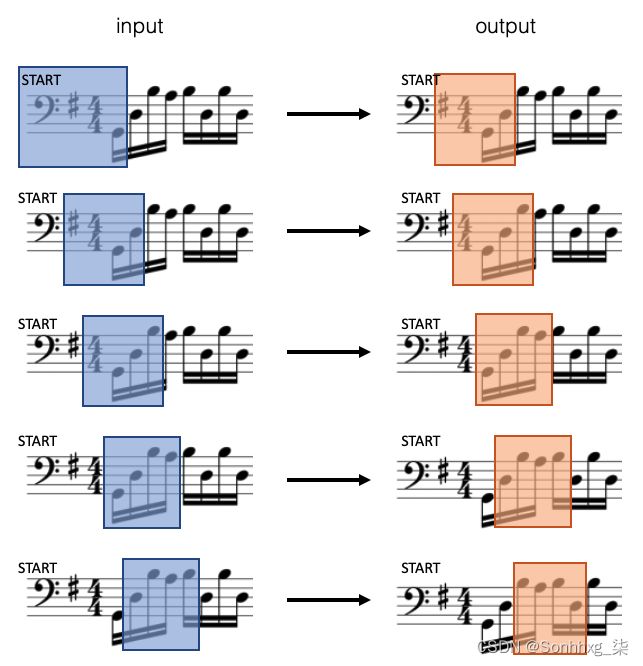
我们通过使用滑动窗口技术将每个序列分成 50 个元素的块来创建训练集。输出只是将输入移位一个音符，因此 Transformer 被赋予预测下一个元素的任务，给定前面的 50 个元素。一个示例（使用仅包含 4 个元素的滑动窗口用于演示目的）显示在图7.4 。

图7.4 音乐生成模型的输入和输出——在此示例中，使用滑动窗口创建长度为 4 的块，然后将其移动一个元素以创建目标输出。

我们将用于 Transformer 的架构与我们在前一章中用于文本生成的架构相同，但有一些关键差异。

正弦位置编码

首先，我们将为令牌位置引入一种不同类型的编码。在上一章中，我们使用了一个简单的Embedding层来编码每个标记的位置——有效地将每个整数位置映射到模型学习的不同向量。因此，我们需要定义序列可能的最大长度 ( N )，并在该序列长度上进行训练。这种方法的缺点是不可能外推到比这个最大长度更长的序列。您必须将输入剪辑到最后N个标记，如果您尝试生成长格式内容，这并不理想。

为了避免这个问题，我们可以改用另一种称为正弦位置嵌入的嵌入。这类似于我们在第 8 章中用于对扩散模型的噪声方差进行编码的嵌入。具体来说，以下函数用于将输入序列中单词 ( pos )的位置转换为长度为d的唯一向量：

对于较小的i，该函数的波长较短，因此函数值沿位置轴快速变化。i值越大，波长越长。因此，每个位置都有自己独特的编码，这是不同波长的特定组合。

请注意，此嵌入是为所有可能的位置值定义的。它是一个确定性函数（即它不是由模型学习的），它使用三角函数为每个可能的位置定义唯一的编码。

Keras NLP 模块有一个内置层，可以为我们实现这种嵌入——因此我们可以定义我们的TokenAndPositionEmbedding层，如下所示。

示例 7-5 ：标记音高和持续时间

class TokenAndPositionEmbedding(keras.layers.Layer):
    def __init__(self, vocab_size, embed_dim):
        super(TokenAndPositionEmbedding, self).__init__()
        self.vocab_size = vocab_size
        self.embed_dim = embed_dim
        self.token_emb = keras.layers.Embedding(input_dim=vocab_size, output_dim=embed_dim)
        self.pos_emb = keras_nlp.layers.SinePositionEncoding()

    def call(self, x):
        embedding = self.token_emb(x)
        positions = self.pos_emb(embedding)
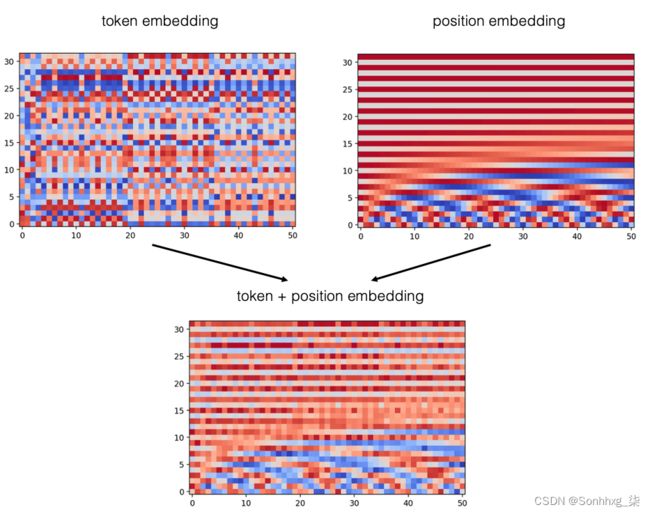
        return embedding + positions

图7.5 显示了如何添加两个嵌入（标记和位置）以生成序列的整体嵌入。

图7.5 该TokenAndPositionEmbedding层将标记嵌入添加到正弦位置嵌入中，以生成序列的整体嵌入。

多个输入和输出

其次，我们现在有两个输入流（音高和持续时间）和两个输出流（预测的音高和持续时间）。因此，我们需要调整 Transformer 的架构来满足这一需求。

有很多方法可以处理双输入流。我们可以创建表示每个音高持续时间对的标记，然后将序列视为单个标记流。然而，这有一个缺点，那就是无法表示在训练集中没有看到的音高-持续时间对（例如，我们可能已经独立地看到一个音符G#2和一个1/3持续时间，但从来没有在一起，所以不会有标记对于G#2:1/3。

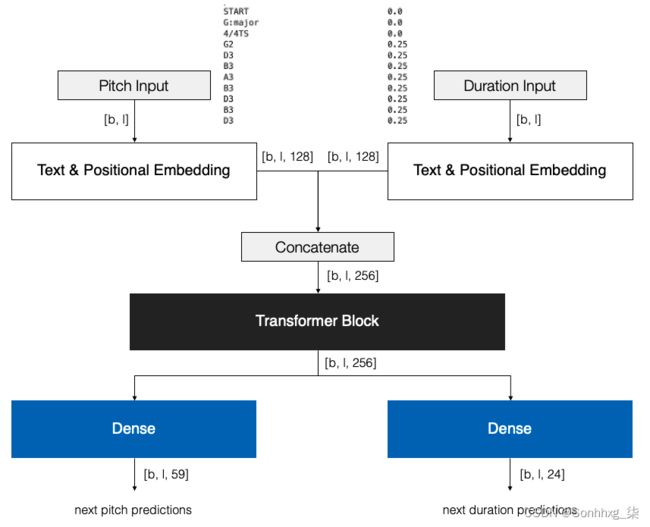
相反，我们选择分别嵌入音高和持续时间标记，然后使用连接层创建可由下游 Transformer 块使用的输入的单一表示。类似地，Transformer 块的输出被传递到两个独立的 Dense 层，它们代表预测的音调和持续时间概率。总体架构如图7.6 所示。

图7.6 音乐生成 Transformer 的架构。图层输出形状显示为批量大小b和序列长度l。

这只是使用 Transformer 处理多个输入和输出的一种方法。也可以在单个输入流中交错音高和持续时间标记，让模型了解输出应该是单个流，其中音高和持续时间标记交替出现。这伴随着确保在模型尚未学会如何正确交错标记时仍然可以解析输出的复杂性。设计模型的方法没有对错之分- 乐趣之一在于尝试不同的设置并查看最适合您的设置！

音乐生成变压器的分析。

我们将从头开始生成一些音乐，通过为网络播种START音高标记和0.0持续时间（即，我们告诉模型假设它是从乐曲的开头开始的）。然后我们可以使用我们在第 6 章中用于生成文本序列的相同迭代技术生成一段音乐，如下所示：

1. 给定当前序列（音高名称和音符时长），模型预测下一个音高和时长的两种分布。

2. 我们从这两种分布中抽样，使用一个temperature参数来控制我们希望在抽样过程中有多少变化。

3. 所选音符被存储，其名称和持续时间附加到相应的输入序列。

4. 对于我们希望生成的尽可能多的音符，使用新的输入序列重复该过程。

图7.7 显示了模型在训练过程的各个阶段从头开始生成的音乐示例。

图7.7 START仅使用令牌和持续时间播种时模型生成的一些段落示例0.0。在这里，我们对音高名称和持续时间使用 0.5 的温度

我们在本节中的大部分分析将集中在音高预测上，而不是节奏上，因为对于巴赫的大提琴组曲来说，和声的复杂性更难捕捉，因此更值得研究。但是，您也可以对模型的节奏预测应用相同的分析，这可能与您可以用来训练该模型的其他音乐风格（例如鼓声）特别相关。

图7.7 中生成的段落有几点需要注意。首先，看看音乐如何随着训练的进行而变得更加复杂。首先，该模型通过坚持使用同一组音符和节奏来确保安全。到 epoch 10，该模型已经开始生成小的音符，到 epoch 20，它正在产生有趣的节奏，并牢固地建立在固定调（降 E 大调）中。

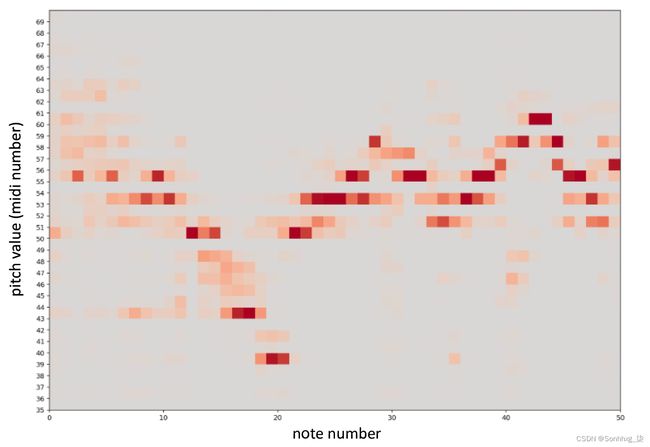
其次，我们可以通过将每个时间步的预测分布绘制为热图来分析音符音高随时间的分布。图 7.8显示了图7.7中第 20 个时期的示例的热图。

图 7.8 可能的下一个音符随时间的分布（在第 20 个时期）：方块越暗，模型越确定下一个音符在这个音高

这里需要注意的一个有趣的一点是，该模型已经清楚地了解了哪些音符属于特定的键，因为在不属于该键的音符处存在分布间隙。例如，音符 54（对应于Gb / F# ）的行有一个灰色间隙。这个音符极不可能出现在降 E 大调的乐曲中。在生成过程的早期，调由模型设置，随着乐曲的进行，模型通过关注代表降 E 大调调的标记来选择更可能出现在该调中的音符。

还值得指出的是，该模型已经学习了巴赫的典型风格，即在大提琴上降到低音以结束一个乐句，然后再次弹回以开始下一个乐句。看看音符 20 左右，乐句如何以降 E 低调结束——这在巴赫大提琴组曲中很常见，然后在下一个乐句开始时返回到乐器的更高、更响亮的音域，这正是模型所采用的预测。低降 E 音（音高编号 39）和下一个音符之间存在较大的灰色间隙，预计下一个音符位于音高编号 50 左右，而不是继续围绕乐器的深度隆隆作响。

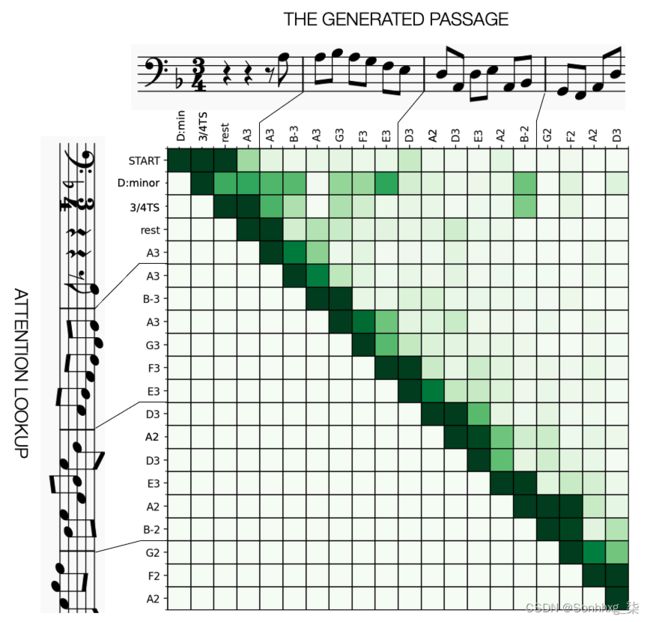
最后，我们应该检查我们的注意力机制是否按预期工作。图7.9 中的横轴显示了生成的音符序列；垂直轴显示了在沿水平轴预测每个音符时网络的注意力瞄准的位置。每个正方形的颜色显示生成序列中每个点的所有头部的最大注意力权重。正方形越暗，序列中的这个位置就越受关注。为简单起见，我们仅在此图中显示了音高，但每个音符的持续时间也由网络关注。

图7.9 矩阵中每个方块的颜色表示在预测水平轴上的音符时，垂直轴上每个位置的注意力。方块越红，给予的关注度越高（最大程度地占据所有头）。

我们可以看到，对于初始密钥签名、时间签名和其余部分，网络选择将几乎所有注意力放在令牌上START。这是有道理的，因为这些人工制品总是出现在一段音乐的开头——一旦音符开始流动，令牌就START基本上不再被关注。

当我们浏览最初的几个音符时，我们可以看到网络将大部分注意力放在大约最后 2-4 个音符上，很少对超过四个音符之前的音符给予显着重视。同样，这是有道理的；前四个注释中可能包含足够的信息来理解该短语如何继续。此外，一些音符更强烈地回到 D 小调的调号 - 例如，E3（乐曲的第 7 个音符）和B-2（降 B - 乐曲的第 14 个音符）。这很吸引人，因为这些正是依靠 D 小调来消除任何歧义的音符。网络必须回头看在调号上，以表明调号中有降 B（而不是自然 B），但调号中没有降 E（必须改用降 E）。

还有一些例子表明网络选择忽略某个音符或在附近休息，因为它不会为它对短语的理解添加任何额外信息。例如，倒数第二个音符（A2）对后面的三个音符不是特别注意B-2，但对后面的四个音符稍微注意一些A2。对于模型来说，更有趣的是查看A2落在节拍上的那个，而不是B-2关闭节拍的，这只是一个经过的音符。

请记住，我们没有告诉模型任何关于哪些音符相关或下面哪些音符与哪些调号相关的信息——它只是通过研究 JS Bach 的音乐自行解决了这个问题。

和弦音乐的标记化

这我们在本节中探讨的 Transformer 适用于单线（单音）音乐，但它能否适用于多线（和弦）音乐？

挑战在于如何将不同的音乐线表示为单个标记序列。在上一节中，我们决定将音符的音高和持续时间拆分为网络的两个不同的输入和输出，但我们也看到我们可以将这些标记交织成一个流。我们可以用同样的想法来处理和弦音乐。我们将在下一节中介绍两种不同的方法——网格标记化和基于事件的标记化，如 2018 年论文 Music Transformer：Generating Music with Long-Term structure ( https://arxiv.org/abs/1809.04281 ) 中所讨论的).

网格标记化

考虑以下 J.S. Bach合唱中的两小节音乐。有四个不同的声部（高音 (S)、中音 (A)、男高音 (T)、低音 (B)），写在不同的五线谱上。

图7.10 J.S. Bach chorale的前两小节。

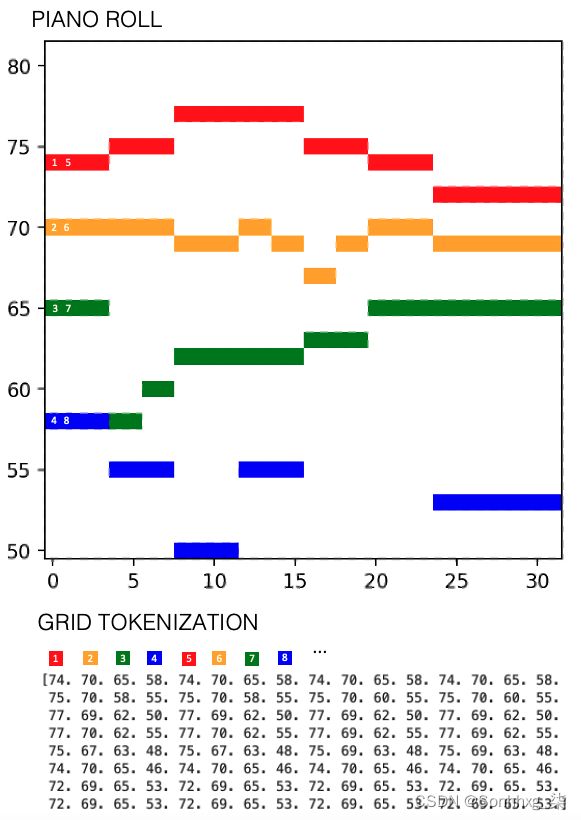
我们可以想象在网格上绘制此音乐，其中 y 轴表示音符的音高，x 轴表示自乐曲开始以来经过的 16 分音符（十六分音符）的数量。如果网格正方形被填满，那么在那个时间点会播放一个音符——所有四个部分都绘制在同一个网格上。这个网格被称为钢琴卷，因为它类似于一个带有孔的物理纸卷，在数字系统发明之前用作记录机制。

我们可以将网格序列化为标记流，方法是先移动四个声部，然后按顺序沿着时间步长移动。这会产生一个标记序列，其中下标表示时间步长，如图7.11 S_1, A_1, T_1, B_1, S_2, A_2, T_2, B_2...所示。

图7.11 为Bach chorale的前两小节创建网格标记化

然后我们将在这个标记序列上训练我们的 Transformer，以在给定先前标记的情况下预测下一个标记。我们可以将生成的序列解码回网格结构，方法是随着时间的推移将序列以 4 个音符为一组（每个音符一个）回滚。这种技术的效果出奇地好，尽管同一个音符经常被分割成多个标记，中间夹杂着来自其他声音的标记。

但是，也有一些缺点。首先，请注意模型无法区分同一音高的一个长音符和两个较短的相邻音符之间的区别。这是因为标记化没有明确编码音符的持续时间 - 仅编码音符是否存在于每个时间步长。

其次，此方法要求音乐具有可分为大小合理的块的规则节拍。例如，使用当前系统，我们无法编码三连音（一组三个音符在一个节拍中演奏）。我们可以将音乐分成每四分音符（四分音符）12 步而不是 4 步，但随后我们将表示相同音乐段落所需的标记数量增加三倍，这是模型训练过程和回顾能力的开销.

最后，我们如何将其他组件添加到标记化中并不明显，例如动态（音乐在每个部分的音量大小）或速度变化。我们被锁定在钢琴卷帘的二维网格结构中，它提供了一种方便的方式来表示音高和时间，但不一定是一种合并其他使音乐听起来有趣的组件的简单方法，例如动态和速度.

基于事件的标记化

一种更灵活的方法是使用基于事件的标记化。这可以被认为是一个词汇表，它使用丰富的标记词汇表从字面上描述音乐是如何作为一系列事件创建的。

例如在图7.12 中，我们使用三种风格的令牌NOTE_ON（开始播放给定的音符pitch）、NOTE_OFF（停止播放给定的音符pitch）和TIME_SHIFT（按给定的时间向前移动step）。该词汇表可用于创建一个序列，该序列将音乐的构造描述为一组指令。

图7.12 Bach chorale第一小节的事件标记化。

我们还可以将其他类型的标记合并到这个词汇表中，以表示后续音符的动态和速度变化。此方法还提供了一种在四分音符的背景下生成三连音的方法，方法是将三连音的音符与TIME_SHIFT<0.33>标记分开。总的来说，它是一个更具表现力的标记化框架，尽管 Transformer 学习训练集音乐中的固有模式也可能更复杂，因为根据定义，它的结构不如网格方法。

我不会使用这些标记化模式构建另一个 Transformer，而是将其作为练习留给读者来解决。相反，我们将把注意力转向另一种生成和弦音乐的方法。

您可能认为图7.11中显示的钢琴卷帘看起来有点像现代艺术作品。这就引出了一个问题——我们真的可以将这个钢琴卷轴视为一张图片并使用图像生成方法而不是序列生成技术吗？

正如我们将在下一节中看到的那样，这个问题的答案是肯定的，我们可以将音乐生成直接视为图像生成问题。这意味着我们可以应用相同的基于卷积的技术，而不是使用 Transformer，这些技术在图像生成问题上非常有效——特别是 GAN。

MuseGAN

这MuseGAN 在 2017 年的论文“MuseGAN: Multi-Track Sequential Generative Adversarial Networks for Symbolic Music Generation and Accompaniment”中被介绍。者展示了如何通过新颖的 GAN 框架训练模型生成和弦、多轨、多小节音乐。此外，他们展示了如何通过划分为发生器提供噪声矢量的职责，他们能够对音乐的高级时间和基于轨道的特征保持细粒度控制。

让我们从准备我们在上一节中使用的 JS Bach 合唱数据集开始。

准备数据

要开始这个项目，您首先需要下载我们将用于训练 MuseGAN 的 MIDI 文件。我们将使用包含 229 首 JS Bach 合唱曲的数据集来表示四种声部。

您可以通过运行图书存储库中的 Bach chorale 数据集下载程序脚本来下载数据集，如示例 7-6 所示。这会将 MIDI 文件本地保存到/data文件夹中。

示例 7-6 ：下载Bach chorale dataset

bash scripts/download_bach_chorale_data.sh

正如我们之前所见，数据集由每个时间步的四个数字组成的数组：四个声音中每个声音的 MIDI 音高。此数据集中的时间步长等于十六分音符（十六分音符）。因此，例如，在 4 个四分之一（四分音符）节拍的单个小节中，有 16 个时间步长。数据集自动拆分为train、validation和test集。我们将使用训练数据集来训练 MuseGAN。

我们首先需要将数据转换成正确的形状以提供给 GAN。在此示例中，我们将生成两小节音乐，因此我们将首先仅提取每首赞美诗的前两小节。每个小节由 16 个时间步长组成，4 个声部3中可能有 84 个音高。

因此，转换后的数据将具有以下形状：

[BATCH_SIZE, N_BARS, N_STEPS_PER_BAR, N_PITCHES, N_TRACKS]

where

BATCH_SIZE = 64 
N_BARS = 2 
N_STEPS_PER_BAR = 16 
N_PITCHES = 84 
N_TRACKS = 4

为了将数据变成这种形状，我们将音高数字一次性编码为长度为 84 的向量，并将每个音符序列分成两组，每组 16 个，以复制 2 个小节。

图7.13 显示了如何将两小节原始数据转换为我们将用于训练 GAN 的转换钢琴卷帘数据集。

图7.13 将两段原始数据处理成我们可以用来训练 GAN 的钢琴卷帘数据。

在我们探索 MuseGAN 架构之前，有足够的时间参观音乐厅，表演即将开始……

The Musical Organ

这指挥在指挥台上敲了两下指挥棒。表演即将开始。在他面前坐着一个管弦乐队。然而，这支管弦乐队并不打算演奏贝多芬交响曲或柴可夫斯基序曲。该管弦乐队在演出期间现场创作原创音乐，完全由一组演奏者向舞台中央的巨大音乐管风琴（简称 MuseGAN）发出指令，将这些指令转化为优美的音乐供观众欣赏. 可以训练管弦乐队以特定风格产生音乐，并且没有两次表演是相同的。

管弦乐队的128名演奏者被分成4个相等的部分，每部分32名演奏者。每个部分都向 MuseGAN 发出指令，并在管弦乐队中有不同的职责。

风格部分负责产生表演的整体音乐风格风格。在许多方面，它是所有部分中最简单的工作，因为每个演奏者只需在音乐会开始时生成一条指令，然后在整个表演过程中不断将其输入 MuseGAN。

groove部分有类似的工作，但每个演奏者都会产生几个指令：一个指令用于MuseGAN 输出的每个不同的音乐声音（或音轨）。例如，律动部分的每个成员都会产生四个指令，每个指令对应女高音、中音、男高音和低音。因此，他们的工作是为每个单独的声音提供节奏，并在整个表演过程中保持不变。

风格和律动部分在整首曲子中都没有改变它们的说明。表演的动态元素由最后两个部分提供，确保音乐随着每个小节的流逝而不断变化。

和弦部分的演奏者在每个小节的开头更改他们的指令。这具有赋予每个小节独特的音乐特征的效果，例如，通过改变和弦。和弦部分的演奏者每小节只产生一个指令，然后应用于每个声部。

旋律部分的演奏者是最累人的工作，因为他们在整首曲子的每个小节开始时对每个声部给出不同的指令。这些演奏者对音乐具有最精细的控制，因此可以将其视为提供旋律趣味的部分。

这样就完成了管弦乐队的描述。我们可以总结出每个部分的职责，如表7-2所示。

表 7-2 ：MuseGAN 管弦乐队的部分

	每个酒吧的说明都不同？	每个声音的指令不同？
风格	Ｘ	Ｘ
槽	Ｘ	✓
和弦	✓	Ｘ
旋律	✓	✓

根据当前的 128 条指令集（每个玩家一条），由 MuseGAN 生成下一段音乐。训练 MuseGAN 做到这一点并不容易。最初，该乐器只会产生可怕的噪音，因为它无法理解应该如何解释指令以产生与真实音乐无法区分的小节。

这就是指挥的用武之地。指挥会告诉 MuseGAN 它正在制作的音乐与真实音乐有明显区别，然后 MuseGAN 会调整其内部布线，以便下次更有可能愚弄指挥。

MuseGAN 演奏者在世界各地巡回演出，在现有音乐足以训练 MuseGAN 的任何风格下举办音乐会。在下一节中，我们将了解如何使用 Keras 构建 MuseGAN，以了解如何生成逼真的和弦音乐。

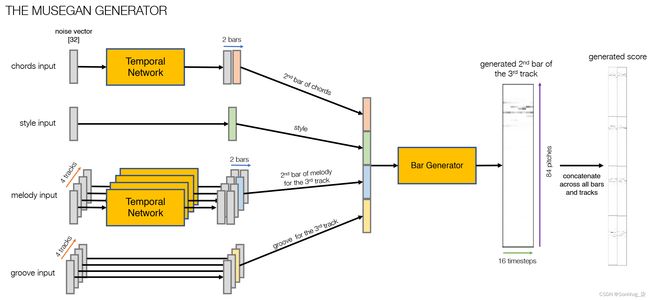
MuseGAN 生成器 - 概述

喜欢与所有 GAN 相比，MuseGAN 由一个生成器和一个评论家组成。生成器试图用它的音乐创作来愚弄评论家，而评论家则试图通过确保它能够分辨出生成器伪造的巴赫合唱曲与真实作品之间的区别来防止这种情况发生。

MuseGAN 的不同之处在于，生成器不仅接受单个噪声向量作为输入，而是有四个独立的输入，对应于故事中管弦乐队的四个部分——和弦、风格、旋律和槽。通过独立操作这些输入中的每一个，我们可以更改生成音乐的高级属性。

图7.14 显示了生成器的高级视图。

图7.14 MuseGAN 生成器的高级图

该图显示了和弦和旋律输入是如何首先通过时间网络传递的，该时间网络输出一个张量，其中一个维度等于要生成的小节数。风格和律动输入不会以这种方式在时间上被拉伸，因为它们在整个乐曲中保持不变。

然后，为了为特定音轨生成特定小节，将来自网络的和弦、风格、旋律和律动部分的相关向量连接起来，形成一个更长的向量。然后将其传递给小节生成器，最终为指定轨道输出指定小节。

通过连接所有曲目的生成的条，我们创建了一个可以与评论家的真实分数进行比较的分数。

我们先来看看如何构建时间网络。

时间网络

每个时间网络的工作是将长度为 32 ( ) 的单个输入噪声向量转换Z_DIM = 32为每个条形图的不同噪声向量（每个条形图的长度也为 32）。实现这一点的方法是使用一个由卷积转置层组成的神经网络，我们称之为时间网络。示例7-7中显示了用于构建它的 Keras 代码。

示例 7-7 ：构建时间网络

def conv_t(x, f, k, s, a, p, bn):
    x = layers.Conv2DTranspose(
                filters = f
                , kernel_size = k
                , padding = p
                , strides = s
                , kernel_initializer = initializer
                )(x)
    if bn:
        x = layers.BatchNormalization(momentum = 0.9)(x)

    x = layers.Activation(a)(x)
    return x

def TemporalNetwork():
    input_layer = layers.Input(shape=(Z_DIM,), name='temporal_input') 
    x = layers.Reshape([1,1,Z_DIM])(input_layer) 
    x = conv_t(x, f=1024, k=(2,1), s=(1,1), a = 'relu', p = 'valid', bn = True) 
    x = conv_t(x, f=Z_DIM, k=(N_BARS - 1,1), s=(1,1), a = 'relu', p = 'valid', bn = True)
    output_layer = layers.Reshape([N_BARS, Z_DIM])(x) 
    return models.Model(input_layer, output_layer)

1.时间网络的输入是一个长度为 32 ( Z_DIM) 的向量。

2.我们将这个向量重新整形为具有 32 个通道的 1×1 张量，以便我们可以对其应用卷积二维转置操作。

3.我们应用Conv2DTranspose层来沿一个轴扩展张量的大小，使其与 的长度相同N_BARS。

4.我们用一层去除了不必要的额外维度Reshape。

我们使用卷积运算而不是要求网络中有两个独立的和弦向量的原因是因为我们希望网络学习一个小节应该如何以一致的方式从另一个小节跟随。使用神经网络沿时间轴扩展输入向量意味着模型有机会了解音乐如何跨小节流动，而不是将每个小节视为完全独立于最后一个小节。

和弦、风格、旋律和律动

现在让我们仔细看看为发电机供电的四个不同输入。

和弦

和弦输入是长度为 的单个噪声向量Z_DIM。这个向量的作用是控制音乐随时间的总体进程，跨音轨共享，所以我们使用 a 将TemporalNetwork这个单个向量转换为每个小节的不同潜在向量。请注意，虽然这被标记为chords输入，但它实际上可以控制关于每小节变化的音乐的任何内容，例如一般节奏风格，而不是特定于任何特定轨道。

风格

样式输入也是一个长度为 的向量Z_DIM。这是在没有转换的情况下进行的，因此在所有小节和曲目中都是一样的。它可以被认为是控制作品整体风格的矢量（即它一致地影响所有小节和曲目）。

旋律

旋律输入是一个形状数组[N_TRACKS, Z_DIM]——也就是说，我们为模型提供Z_DIM每个音轨长度的随机噪声向量。

这些向量中的每一个都通过特定于轨道的 传递TemporalNetwork，其中权重不在轨道之间共享。Z_DIM输出是每个轨道的每个小节的长度向量。因此，该模型可以使用这些输入向量来独立微调每个条形和轨道的内容。

槽

凹槽输入也是一个形状数组——每个轨道[N_TRACKS, Z_DIM]长度的随机噪声向量。Z_DIM与旋律输入不同，这些不通过时间网络传递，而是直接通过，就像风格向量一样。因此，每个凹槽矢量都会影响轨道的所有小节的整体属性。

MuseGAN 生成器的最后一个部分是小节生成器——让我们看看如何使用它来将和弦、风格、旋律和律动组件的输出粘合在一起。

The Bar Generator

这小节生成器接收四个潜在向量——每个向量来自和弦、风格、旋律和律动成分。这些被连接起来产生一个长度的向量4 * Z_DIM作为输入。输出是单个音轨的单个小节的钢琴卷轴表示，即形状为 的张量[1, n_steps_per_bar, n_pitches, 1]。

小节生成器只是一个神经网络，它使用卷积转置层来扩展输入向量的时间和音高维度。我们为每个轨道创建一个条形生成器，轨道之间不共享权重。示例 7-8BarGenerator中给出了构建 a 的 Keras 代码。

示例 7-8 ：建立BarGenerator

def BarGenerator():

    input_layer = layers.Input(shape=(Z_DIM * 4,), name='bar_generator_input') 

    x = layers.Dense(1024)(input_layer) 
    x = layers.BatchNormalization(momentum = 0.9)(x)
    x = layers.Activation('relu')(x)
    x = layers.Reshape([2,1,512])(x)

    x = conv_t(x, f=512, k=(2,1), s=(2,1), a= 'relu',  p = 'same', bn = True) 
    x = conv_t(x, f=256, k=(2,1), s=(2,1), a= 'relu', p = 'same', bn = True)
    x = conv_t(x, f=256, k=(2,1), s=(2,1), a= 'relu', p = 'same', bn = True)
    x = conv_t(x, f=256, k=(1,7), s=(1,7), a= 'relu', p = 'same',bn = True) 
    x = conv_t(x, f=1, k=(1,12), s=(1,12), a= 'tanh', p = 'same', bn = False) 

    output_layer = layers.Reshape([1, N_STEPS_PER_BAR , N_PITCHES ,1])(x) 

    return models.Model(input_layer, output_layer)
BarGenerator().summary()

1.条形生成器的输入是长度为 的向量4 * Z_DIM。

2.通过一层后Dense，我们重塑张量，为卷积转置操作做好准备。

3.首先我们沿着时间轴展开张量……

4.… 然后沿着俯仰轴。

5.最后一层应用了 tanh 激活，因为我们将使用 WGAN-GP（需要 tanh 输出激活）来训练网络。

6.张量被重塑以添加两个额外的大小为 1 的维度，以准备与其他条形和轨道连接。

MuseGAN 生成器 - 将它们放在一起

最终，MuseGAN 拥有一个包含所有时间网络和条形生成器的单一生成器。该网络采用四个输入并将它们转换为多轨、多条乐谱。这示例 7-9中提供了构建整个生成器的 Keras 代码。

示例 7-9 ：构建 MuseGAN 生成器

def Generator():
    chords_input = layers.Input(shape=(Z_DIM,), name='chords_input') 
    style_input = layers.Input(shape=(Z_DIM,), name='style_input')
    melody_input = layers.Input(shape=(N_TRACKS, Z_DIM), name='melody_input')
    groove_input = layers.Input(shape=(N_TRACKS, Z_DIM), name='groove_input')

    # CHORDS -> TEMPORAL NETWORK
    chords_tempNetwork = TemporalNetwork() 
    chords_over_time = chords_tempNetwork(chords_input) # [n_bars, z_dim]

    # MELODY -> TEMPORAL NETWORK
    melody_over_time = [None] * N_TRACKS # list of n_tracks [n_bars, z_dim] tensors
    melody_tempNetwork = [None] * N_TRACKS
    for track in range(N_TRACKS):
        melody_tempNetwork[track] = TemporalNetwork() 
        melody_track = layers.Lambda(lambda x, track = track: x[:,track,:])(melody_input)
        melody_over_time[track] = melody_tempNetwork[track](melody_track)

    # CREATE BAR GENERATOR FOR EACH TRACK
    barGen = [None] * N_TRACKS
    for track in range(N_TRACKS):
        barGen[track] = BarGenerator() 

    # CREATE OUTPUT FOR EVERY TRACK AND BAR
    bars_output = [None] * N_BARS
    c = [None] * N_BARS
    for bar in range(N_BARS): 
        track_output = [None] * N_TRACKS

        c[bar] = layers.Lambda(lambda x, bar = bar: x[:,bar,:])(chords_over_time)  # [z_dim]
        s = style_input # [z_dim]

        for track in range(N_TRACKS):

            m = layers.Lambda(lambda x, bar = bar: x[:,bar,:])(melody_over_time[track]) # [z_dim]
            g = layers.Lambda(lambda x, track = track: x[:,track,:])(groove_input) # [z_dim]

            z_input = layers.Concatenate(axis = 1, name = 'total_input_bar_{}_track_{}'.format(bar, track))([c[bar],s,m,g])

            track_output[track] = barGen[track](z_input)

        bars_output[bar] = layers.Concatenate(axis = -1)(track_output)

    generator_output = layers.Concatenate(axis = 1, name = 'concat_bars')(bars_output) 

    return models.Model([chords_input, style_input, melody_input, groove_input], generator_output) 

generator = Generator()

1.生成器的输入已定义。

2.通过时间网络传递和弦输入。

3.通过时间网络传递旋律输入。

4.为每个轨道创建一个独立的条形生成器网络。

5.循环轨道和条形图，为每个组合创建一个生成的条形图。

6.将所有内容连接在一起以形成单个输出张量。

7.MuseGAN 模型将四个不同的噪声张量作为输入并输出生成的多轨、多条分数。

MuseGAN 评论家

在与生成器相比，critic 架构要简单得多（GAN 通常就是这种情况）。

评论家试图将生成器创建的完整多轨、多小节乐谱与巴赫合唱团的真实例外区分开来。它是一个卷积神经网络，主要由将Conv3D分数折叠成单个输出预测的层组成。到目前为止，我们只处理了Conv2D图层，适用于三维输入图像（宽度、高度、通道）。这里我们必须使用Conv3D层，它类似于Conv2D层但接受四维输入张量 ( n_bars, n_steps_per_bar, n_pitches, n_tracks)。

此外，我们不在 critic 中使用批量归一化层，因为我们将使用 WGAN-GP 框架来训练 GAN，这禁止这样做。

示例 7-10中给出了构建评论家的 Keras 代码。

示例 7-10 ：建立 MuseGAN critic

def conv(x, f, k, s, p):
    x = layers.Conv3D(filters = f
                , kernel_size = k
                , padding = p
                , strides = s
                , kernel_initializer = initializer
                )(x)
    x = layers.LeakyReLU()(x)
    return x

def Critic():
    critic_input = layers.Input(shape=(N_BARS, N_STEPS_PER_BAR, N_PITCHES, N_TRACKS), name='critic_input') 

    x = critic_input
    x = conv(x, f=128, k = (2,1,1), s = (1,1,1), p = 'valid') 
    x = conv(x, f=128, k = (N_BARS - 1,1,1), s = (1,1,1), p = 'valid')

    x = conv(x, f=128, k = (1,1,12), s = (1,1,12), p = 'same') 
    x = conv(x, f=128, k = (1,1,7), s = (1,1,7), p = 'same')

    x = conv(x, f=128, k = (1,2,1), s = (1,2,1), p = 'same') 
    x = conv(x, f=128, k = (1,2,1), s = (1,2,1), p = 'same')
    x = conv(x, f=256, k = (1,4,1), s = (1,2,1), p = 'same')
    x = conv(x, f=512, k = (1,3,1), s = (1,2,1), p = 'same')

    x = layers.Flatten()(x)

    x = layers.Dense(1024, kernel_initializer = initializer)(x)
    x = layers.LeakyReLU()(x)

    critic_output = layers.Dense(1, activation=None, kernel_initializer = initializer)(x) 

    return models.Model(critic_input, critic_output)

critic = Critic()

1.评论家的输入是一组多轨、多条分数，每个分数都是 shape [N_BARS, N_STEPS_PER_BAR, N_PITCHES, N_TRACKS]。

2.首先，我们沿条轴折叠张量。Conv3D我们在处理 4D 张量时在整个 critic 中应用层。

3.接下来，我们沿着俯仰轴折叠张量。

4.最后，我们沿着时间步轴折叠张量。

根据 WGAN-GP 框架的要求，输出是Dense一个只有一个单元且没有激活函数的层。

MuseGAN分析

我们可以使用我们的 MuseGAN 进行一些实验，方法是生成一个分数，然后调整一些输入噪声参数以查看对输出的影响。

生成器的输出是 [–1, 1] 范围内的值数组（由于最后一层的 tanh 激活函数）。为了将其转换为每个音轨的单个音符，我们选择每个时间步长的所有 84 个音高中具有最大值的音符。在最初的 MuseGAN 论文中，作者使用了 0 的阈值，因为每个音轨可以包含多个音符；然而，在这个设置中，我们可以简单地取最大值，以保证每个音轨每个时间步长一个音符，就像巴赫合唱团的情况一样。

图7.15 显示了模型从随机正态分布的噪声向量（左上角）生成的分数。我们可以在数据集中找到最接近的分数（通过欧氏距离）并检查我们生成的分数不是数据集中已经存在的一段音乐的副本——最接近的分数显示在它的正下方，我们可以看到它不像我们生成的分数。

图7.15 MuseGAN 预测分数示例，显示训练数据中最接近的真实分数以及生成的分数如何受到输入噪声变化的影响

现在让我们尝试使用输入噪声来调整我们生成的分数。首先，我们可以尝试改变和弦噪声向量——图 7.15 中左下角的乐谱显示了结果。我们可以看到，每条轨道都发生了变化，正如预期的那样，而且这两个条形图表现出不同的属性。在第二个小节中，基线更有活力，顶线的音调比第一个小节高。这是因为影响两个小节的潜在向量不同，因为输入和弦向量是通过时间网络传递的。

当我们更改样式向量（右上角）时，两个条形图的变化方式相似。整个段落以一致的方式改变了原始生成乐谱的风格（即使用相同的潜在向量来调整所有曲目和小节。）

我们还可以通过旋律和律动输入单独改变音轨。在图7.15 中，我们可以看到仅更改顶行音乐的旋律噪声输入的效果。所有其他部分不受影响，但顶线注释发生了显着变化。此外，我们可以看到顶行中两个小节之间的节奏变化：第二个小节更有活力，包含比第一个小节更快的音符。

最后，图中右下角的分数显示了当我们仅为基线更改凹槽输入参数时的预测分数。同样，所有其他部分不受影响，但基线不同。此外，正如我们预期的那样，基线的整体模式在条形图之间保持相似。

由此可见如何使用每个输入参数直接影响生成的音乐序列的高级特征，就像我们在前几章中调整 VAE 和 GAN 的潜在向量以改变生成的音乐序列的外观一样图像。该模型的一个缺点是必须预先指定要生成的柱数。为了解决这个问题，作者展示了模型的扩展，允许将之前的柱作为输入馈入，因此允许模型通过不断将最新预测的柱作为附加输入反馈回模型来生成长格式分数。

概括

在本章中，我们探索了两种不同的音乐生成模型：Transforer 和 MuseGAN。

Transformer 在设计上类似于我们在第6章中看到的用于文本生成的网络。音乐和文本生成有很多共同的特征，并且通常可以将相似的技术用于两者。我们通过为音调和持续时间合并两个输入和输出流来扩展 Transformer 架构。我们看到了模型如何能够通过学习准确地生成巴赫音乐来学习键和音阶等概念。

然后，我们探索了如何调整标记化过程来处理和弦（多轨）音乐生成。网格标记化序列化乐谱的钢琴卷帘表示，使我们能够在单个标记流上训练 Transformer，该标记流以离散的、等间隔的时间步长间隔描述每个声音中存在的音符。基于事件的标记化生成一个配方，描述如何通过单个指令流以顺序方式创建多行音乐。这两种方法各有利弊——基于 Transformer 的音乐生成方法的成功或失败通常在很大程度上取决于标记化方法的选择。

我们还看到生成音乐并不总是需要顺序方法——MuseGAN 使用卷积来生成具有多个音轨的和弦乐谱，方法是将乐谱视为图像，其中音轨是图像的各个通道。MuseGAN 的新颖之处在于四个输入噪声向量（和弦、风格、旋律和律动）的组织方式，因此可以保持对音乐高级特征的完全控制。虽然底层的协调仍然不如巴赫那样完美或多变，但这是对这个极难掌握的问题的一次很好的尝试，并突出了 GAN 解决各种问题的能力。

在下一章中，我们将介绍近年来生成模型最有趣的应用之一，即它们在世界模型中的应用。在介绍世界模型概念的开创性论文中，作者展示了如何建立一个模型，使汽车能够通过首先在其自己生成的环境“梦想”中测试策略来绕着模拟赛道行驶。这使得汽车无需尝试就可以在赛道上行驶，因为它已经想象过如何在自己想象的世界模型中成功地完成这项任务。