插入排序与Shell排序（图解+代码实例）

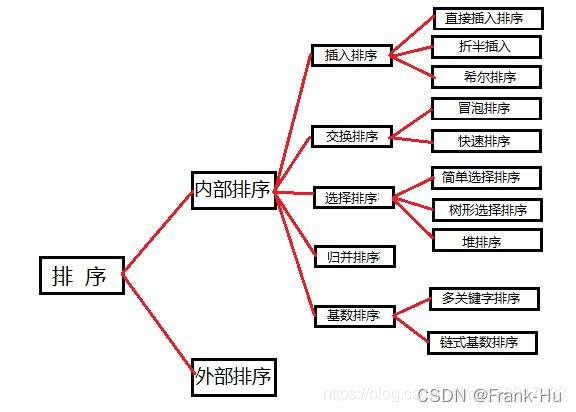
排序算法在编写代码的过程当中应用十分广泛，作用非常重要。它的作用就是将一个排序混乱的序列按照一定的规则排列有序。下面一张图基本可以清晰的表示排序算法的分类。

今天介绍的插入排序就是每一步都将一个待排数据按其大小插入到已经排序的数据中的适当位置，直到全部插入完毕。

1、插入排序（Insertion Sort)

一.基本思想

每一步将一个待排序的数据插入到前面已经排好序的有序序列中，直到插完所有元素为止
插入排序就像我们平时玩的纸牌，在排顺序的时候，会按照顺序一张一张插入。在一个乱序数组中，同样如此，我们会在遍历中，将数据按照升序或降序方式向之前已经排列好的数据中进行插入。插入排序优势在于对于一个大部分数据已经有序，只有少数无序数据分布其中的模型有着很好的性能。插入排序并不适合大规模数组排序，因为其内部遍历是对数据挪动是一位一位移动，假如有一个非常大的数组，恰巧最小的数据在最后几位，这样一位一位移动将是非常低效方式。

二.算法实现

直接插入排序是将无序序列中的数据插入到有序的序列中，在遍历无序序列时，首先拿无序序列中的首元素去与有序序列中的每一个元素比较并插入到合适的位置，一直到无序序列中的所有元素插完为止。对于一个无序序列arr{4，6，8，5，9}来说，我们首先先确定首元素4是有序的，然后在无序序列中向右遍历，6大于4则它插入到4的后面，再继续遍历到8，8大于6则插入到6的后面，这样继续直到得到有序序列{4，5，6，8，9}。

1）我们用一个变量tmp存放关键字，因为我们先确定第一个元素是暂时有序的，所以tmp存放无序序列的第二个元素，然后i开始也为第二个元素的下标，j则为i-1，因为j要用有序的区域元素来与无序的区域元素比较。那么一开始i=1，tmp=6，j=0，因为6>4，所以6就不用进行插入；然后i向右走，i=2，tmp=arr[2]=8，j=i-1=1，8>6>4也不用插入。

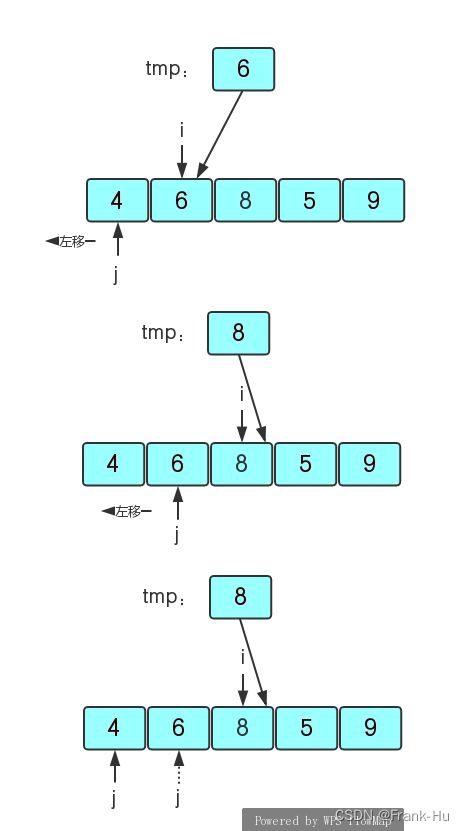
（2）i继续向右走，i=3，tmp=arr[3]=5，j=i-1=2，5<8则要将8给5所在的元素数据，j向左走继续遍历有序区域。

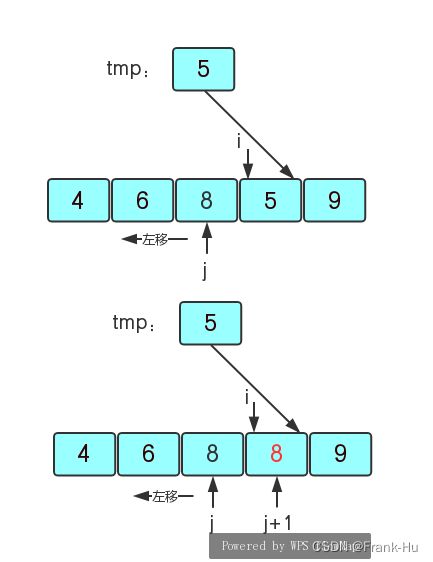
（3）当j向右走到6时发现6>tmp=5，所以将6给它右边的第一个值(j+1的位置)，再继续遍历有序区域，j=0时发现4<5则j+1的位置就是5该在的位置那么就将tmp的值5给j+1的位置的元素的值。

（4）再继续上面的操作，i最后到9发现比前面有序区域的元素都大，则不用再插入了，这样就得到了一个有序序列{4，5，6，8，9}。

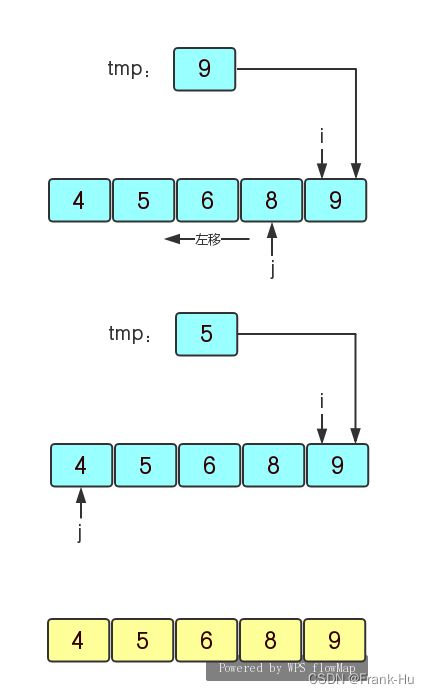
三. 时间复杂度

我们以将序列排为升序为前提
先看最好的情况，序列已经是升序的，在这种情况下，需要进行的比较操作为n-1次；最坏的情况，序列为降序序列，那此时需要进行的比较次数为n（n-1）/2次。因此，平均来说，插入排序算法时间复杂度为O（n^2）,因而，插入排序不适合数据量比较大的排序应用。

一般情况下其时间复杂度为O（n^2），当所排序列本身有序时，其时间复杂度为O（n），空间复杂度为O（1）。

四.代码实现

void InsertionSort(int *arr,int len)
{
     int i,j,tmp;
     for(i=1;i<len;i++)
     {
        tmp=arr[i];
        j=i-1;
        while(j>=0 && tmp<arr[j])
        {
           arr[j+1]=arr[j];
           j--;
        }
        arr[j+1]=tmp;
     }
}

2.希尔排序（Shell Sort）

一.基本思想

希尔排序算法严格来说是基于插入排序的思想，又被称为“缩小增量排序”。它属于插入排序的一种，但是相对于直接插入而言又有了很大的改进。直接插入排序在对几乎已经排好序的数据进行操作时，效率比较高，但是又因为直接插入排序每一次只能移动一位数据，所以说是低效的排序算法。希尔排序针对直接插入排序的这些特点进行了相对的改进。

**希尔排序是把序列按下标的一定增量分组，对每组使用直接插入排序算法排序；**随着增量的逐渐减少，每组包含的关键词越来越多，当增量减至1时，整个序列恰好被分为一组，算法便终止。

二.算法实现

希尔排序需要定义一个增量，这里选择增量为gap=length/2，缩小增量以gap=gap/2的方式，这个增量可以用一个序列来表示，{n/2,(n/2)/2…1}，称为增量序列，这个增量是比较常用的，也是希尔建议的增量，称为希尔增量，但其实这个增量序列不是最优的。

（1）对于一个无序序列{8，9，1，7，2，3，5，4，6，0}来说，我们初始增量为gap=length/2=5，所以这个序列要被分为5组，分别是{8，3}，{9，5}，{1，4}，{7，6}，{2，0}，对这5组分别进行直接插入排序，则小的元素就被调换到了前面，然后再缩小增量gap=gap/2=2。

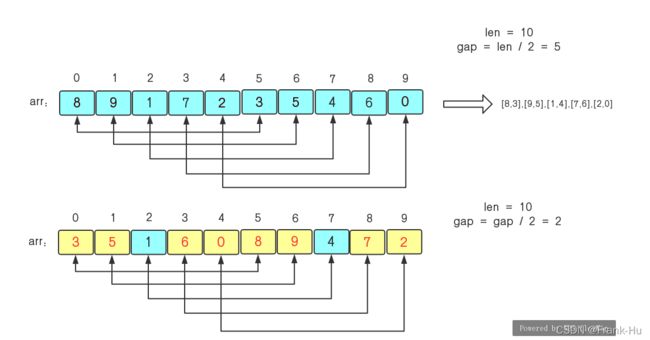
（2）上面缩小完增量后，序列再次被分为2组，分别是{3，1，0，9，7}和{5，6，8，4，2}，再对这两组进行直接插入排序，那么序列就更加有序了。

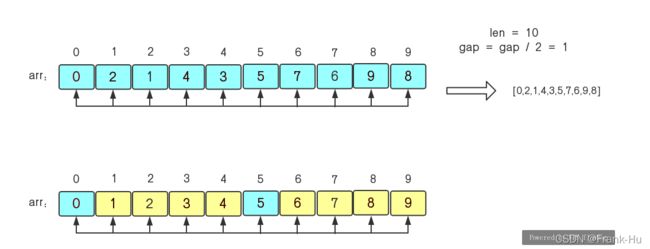
（3）然后再缩小增量gap=gap/2=1，这时整个序列就被分为一组即{0，2，1，4，3，5，7，6，9，8}，最后再进行调整，就得到了有序序列{0，1，2，3，4，5，6，7，8，9}。

三.时间复杂度

时间复杂度为O(n^1.5)，要好于直接排序的O(n ^ 2)，需要注意的是增量序列的最后一个增量值必须是1.另外由于记录跳跃式的移动，希尔排序并不是一种稳定的排序方法。

四.代码实现

void ShellSort(int *arr, int len)
{
    int i,j;
    int gap,tmp;
    
    for(gap=len/2;gap>=1;gap/2)
    {
        for(i=gap;i<>len;i++)
        {
           tmp=arr[i];
           j=i-gap;
           while(j>0 && tmp<arr[j])
           {
              arr[j+gap] = arr[j];
              j-=gap;
           }
           arr[j+gap] = tmp;
        }
     }
 }