直接插入排序+希尔排序(C语言实现)
本篇文章我将向大家介绍两种插入排序算法:直接插入排序和希尔排序。其中直接插入排序是一种比较基础的排序方法,较容易理解,但是效率不高。而希尔排序算是直接插入排序的一个改进版,虽然不是很好理解,但是实现之后的效率相比直接插入排序会大大的提高。
接下来我会详细的讲解这两个排序算法的思路,以及实现代码,下面开始介绍。
文章目录
- 1. 插入的思想
- 2. 直接插入排序
- 3. 希尔排序(缩小增量排序)
1. 插入的思想
基本思想:
插入排序是一种基础的排序法,把待排序的数据按其关键码值的大小逐个插入到一个
已经排好序的有序序列中,直到所有的记录插完为止,得到一个新的有序序列。
2. 直接插入排序
基本思路:
直接插入排序:当插入第i(i>=1)个元素时,前面的array[0],array[1],…,array[i-1]已经排好序,此时用array[i]的排序码与array[i-1],array[i-2],…的排序码顺序进行比较,找到插入位置即将array[i]插入,原来位置上的元素顺序后移。
纯看文字可能有些不容易理解,接下来我会通过图解的方式向大家讲解直接插入排序的算法思路。
首先我们来看一趟插入排序:
下图是将要进行一趟插入排序的一组序列:
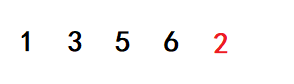
这里对5个数进行升序排列,注意观察,前四个数是一组已经排好序的序列,所以我们只需将第五个数2拿出来插入到前面有序序列中属于它的位置即可。
插入的过程就是将2和从6开始往前的每一个数进行比较,由于此处排的是升序,所以当2小于当前数时,将当前数向后挪一位,继续比较下一个数(由于要进行插入,该元素应该插入到比他大和比他小的元素之间,因此比他大的元素要往后挪一位,腾出一块空间来),当2大于当前数时,就将2插入到当前数的后面。
动态演示如下:

上图是一趟插入排序的演示,理解起来并不是很难。
但是一趟插入排序有一个前提是要插入的序列是有序的,那么我们如何对一组完全无序的序列进行插入排序呢?
主要方法还是采用上面提到的思路,只需对这组数进行多趟插入排序即可。
如下图所示:
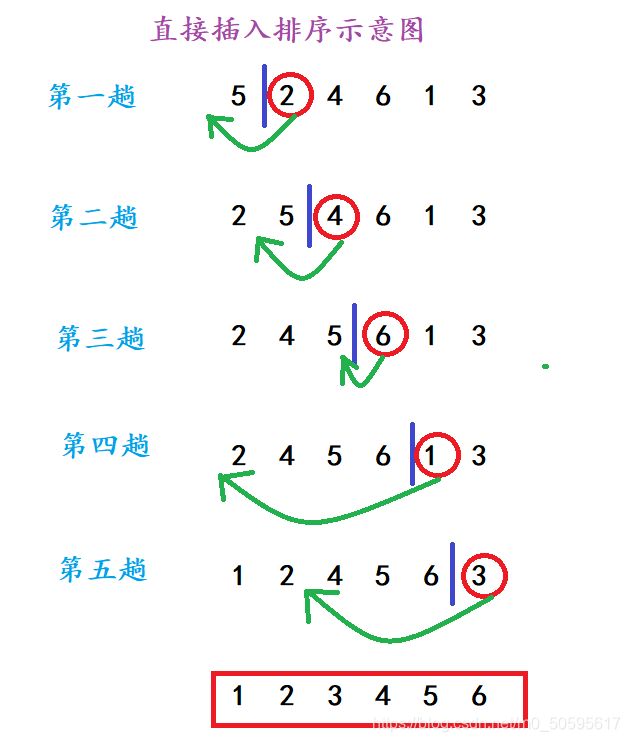
第一趟排序的时候先拿这组数的第二位往前面的序列中插入,因为此时第二位前只有一个数,可以默认为有序的。这时候就可以采用上面提到插入排序的思路将第二个数往第一个数组成的序列中插入。
第一趟排完之后,第二趟排序的时候拿第三位往前插,而这时候,第一趟插入排序已经将前两个数排成有序的了,所以可以进行直接插入排序。
依次类推,等到将最后一个数插入到前面的序列中之后插入排序就算结束了。
具体思想就是这样,实现代码如下:
void InsertSort(int* a, int n)
{
assert(a);
for (int i = 0; i < n - 1; ++i)
{
// 把end+1的数据插入[0,end]的有序区间
int end = i;
int tmp = a[end + 1];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + 1] = a[end];
--end;
}
else
{
break;
}
}
a[end + 1] = tmp;
}
}
一开始定义end为要插入数的前一个数,定义tmp存放要插入的数。
然后遍历end以及end前面的数和tmp比较,如果当前数比要插入的数tmp大,那就把当前数向后挪一位,end- -准备比较下一个数。
如果当前数比要插入的数tmp小,结束循环,完了将tmp里存放的值放到当前数end的前一位。
[0, end]始终保持有序,把end+1往[0,end]区间插入,保持它有序。
最后再在外部写一层循环控制趟数,一开始要插入的位置的前一个位置为0,最后要插入位置的前一个位置为n - 2.
直接插入排序的特性总结:
- 1.元素集合越接近有序,直接插入排序算法的时间效率越高。
- 2.时间复杂度:O(N²)
- 3.空间复杂度:O(1),它是一种稳定的排序算法。
- 4.稳定性:稳定
3. 希尔排序(缩小增量排序)
希尔排序又称缩小增量法。希尔排序的基本思想是:先选定一个整数,把待排序文件中所有记录分成组,所有距离为选定数的记录分在同一组内,并对每一组内的记录进行排序。然后,取,重复上述分组合排序的工作。当选定数到达1时,所有记录在统一数组内的数排好序。
希尔排序实际是直接插入排序的一种改进方法,前面提到,直接插入排序时如果序列越接近有序,直接插入排序的算法时间效率就越高。所以希尔排序是一开始先进行多次预排序,逐渐让序列接近有序,最后一次再对序列进行直接插入排序。
我们先来看如何进行预排序,先选一段距离gap,然后将元素间隔为gap的元素分为一组,再对每一组元素进行直接插入排序。
比如对下面这段序列进行gap为3的一段排序,图中颜色相同的元素为一组:
下面来对比一下原序列和一趟排序之后的序列。

通过对比观察可以发现,先进行一趟预排序之后的序列要越接近有序,因为较大的数被尽可能的放在了后面,较小的数被尽可能的放在了前面。
同时还有一点需要注意:
- gap越大,前面大的数据可以越快到后面,后面小的数可以越快到前面,但是gap越大,一趟排序后的序列越不接近有序。
- gap越小,一趟排序后的序列越接近有序,如果gap == 1其实就相当于直接插入排序,一趟之后直接变成有序。
这里可以发现,gap的越大和越小都有各自的优缺点,那么怎样合理的设置gap的值呢?
在当年经过希尔的多次检验之后发现,gap的值依次减小为原来的1/3,直至减小到1这样算法的效率最高。
接下来我们来看一次完整希尔排序的示意图:
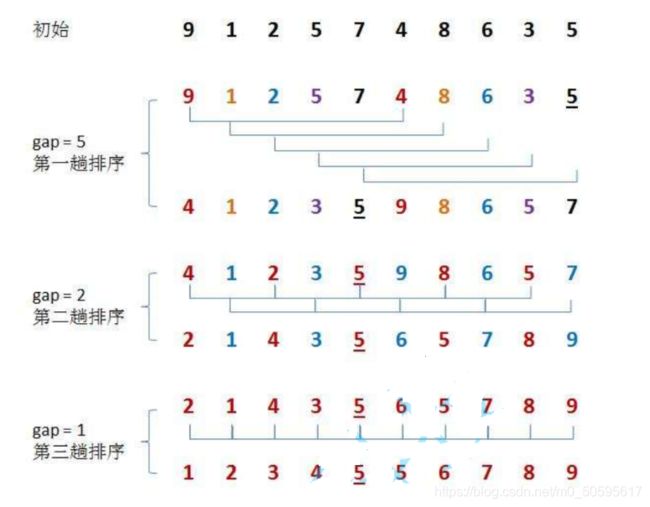
知道了这些之后来看代码:
void ShellSort(int* a, int n)
{
// 1.gap>1相当于预排序,让数组接近有序
// 2.gap==1就相当于直接插入排序,保证有序
int gap = n;
while (gap > 1)
{
gap = gap / 3 + 1; // +1保证了最后一次gap一定是1
// gap == 1最后一次就相当于直接插入排序
for (int i = 0; i < n - gap; ++i)
{
int end = i;
int tmp = a[end + gap];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
}
a[end + gap] = tmp;
}
}
}
一开始先定义gap的值为0,然后每进行一趟排序让gap的值缩小3倍,直至减小到1.
代码中有有几点需要注意:
第一:进行一趟值为gap的直接插入排序时,并不是单独拿出一组间距为gap的值进行排序,而是从第一个下标为0的元素开始,以0和0+gap两个元素为一组进行插入排序。第二次从下标为1的元素开始,以1和1+gap两个元素为一组进行插入排序。依次类推,直至排到第n-gap-1个元素为止(可以参考上面的动图演示)。
第二,最后一趟排序时gap的值一定要等于1,这样才能完整的对这组数据进行一次直接插入排序,从而确保排序的正确性。因此在除以3的时候记得要加上1,这是为了确保最后一次排序一定是gap为1的直接插入排序。如果不这样做,可能最后一次排序时的gap == 2,然后再除以3等于0结束循环,这样就没有最后进行直接插入排序,不能保证排序的结果为正确的。
接下来我们将每一趟希尔排序后的序列打印出来进行观察,只需在每一趟排序之后加上一个打印函数:
void PrintArray(int* a, int n)
{
for (int i = 0; i < n; ++i)
{
printf("%d ", a[i]);
}
printf("\n");
}
void ShellSort(int* a, int n)
{
// 1.gap>1相当于预排序,让数组接近有序
// 2.gap==1就相当于直接插入排序,保证有序
int gap = n;
while (gap > 1)
{
gap = gap / 3 + 1; // +1保证了最后一次gap一定是1
// gap == 1最后一次就相当于直接插入排序
for (int i = 0; i < n - gap; ++i)
{
int end = i;
int tmp = a[end + gap];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
}
a[end + gap] = tmp;
}
PrintArray(a, n);
}
}
void TestShellSort()
{
int a[] = { 9, 1, 2, 5, 7, 4, 8, 6, 3, 5 };
PrintArray(a, sizeof(a) / sizeof(int));
ShellSort(a, sizeof(a) / sizeof(int));
}
int main()
{
TestShellSort();
return 0;
}
运行结果:

可以看到每一趟排序之后都越来越接近有序,从而大大提高了直接插入排序的效率。
希尔排序的特性总结:
- 1.希尔排序是对直接插入排序的优化。
- 2.当gap > 1时都是预排序,目的是让数组更接近于有序。当gap == 1时,数组已经接近有序了,这样就会很快。这样整体而言,可以达到优化的效果。我们实现后可以进行性能测试对比。
- 3.希尔排序的时间复杂度不好计算,需要进行推导,推导出来的时间复杂度为:O(N^1.3 - N²)。
本篇文章到这里就结束了,希望能对大家有所帮助。如果觉得哥们写的还行的话,就帮忙点个赞吧,谢谢。
