SIGGRAPH 2023 - 3D Gaussian Splatting 论文阅读笔记

ArXiv link：https://arxiv.org/abs/2308.04079

3D Gaussian Splatting for Real-Time Radiance Field Rendering

1. 动机

1. 实现高视觉质量的神经辐射场方法仍然需要训练和呈现成本高昂的神经网络，而最近的更快方法不可避免地会权衡质量的速度。（总结：高质量和低成本不可兼得）
2. 对于无界和完整的场景（而不是孤立的对象）和 1080p 分辨率渲染，当前的方法无法实现实时渲染（real-time rendering）

Nerf的一些固有问题：

1. 对场景没有显示表达（如：点云、mesh），而是基于volumetric ray-marching来优化MLP模型。迄今为止最有效的辐射场解决方案通过插值存储在例如体素、hash、网格或点中的value来构建连续表示。虽然这些方法的连续性质有助于优化，但是渲染所需的随机采样是昂贵的，并可能导致噪声。所以我们提出的新方法，结合了两个世界的优点：我们的3D高斯表示允许与最先进的视觉质量和具有竞争力的训练时间进行优化，而我们基于tile-based splatting解决方案确保了在几个先前发布的数据集上以1080p分辨率的sota质量进行实时渲染。

2. 创新点

• 高视觉质量：首先，从相机校准期间产生的系数点开始，我们用3D高斯表示场景，这些高斯保留了连续的volumetric radiance fields的理想属性以进行场景优化，同时避免了空间中不必要的计算。
• 1080p分辨率实时渲染性能（>=30fps）：这种性能的关键是一种新颖的3D高斯场景表示和实时可微渲染器，它为场景优化和新颖的视图合成提供了显著的加速；

3. 方法

1. 3D Gaussians：输入是多视角图片，然后使用SfM过程产生的稀疏点云初始化3D高斯，对比那些需要MVS生成稠密点云的方法，我们获得更高质量的结果只基于SfM点云作为输入，3D高斯是可微的体积表示，也可以通过投影到2D并使用标准的alpha-blending来有效的栅格化，使用相同的图像模型类似NeRF。
2. 第二个我们方法的组成部分是优化3D高斯的属性：3D位置、不透明度、各向异性协方差（anisotropic covariance）和球面调和（SH）系数，同时在优化过程中自适应控制高斯密度，在优化过程中偶尔添加或者删除3D高斯。
3. 第三个也是最后一个元素，是我们实时渲染的解决方案，它使用快速GPU排序算法(sorting algorithm)，并受到基于tile的光栅化（tile-based rasterization）的启发。也受益于3D高斯表达，我们可以可以执行可见性排序的各向异性溅射（splatting）- 这归功于排序和alpha-blending - 并通过跟踪尽可能多的排序splat的遍历来实现快速准确的后向传递。

3.1 可微分的3D高斯溅射

输入是SfM的稀疏点云，不带法线（normal），我们将几何图形建模为一组不需要法线的3D高斯。我们的高斯由世界空间中定义的完整3D协方差矩阵 $\Sigma$ 定义，以点为中心(mean $\mu$)：

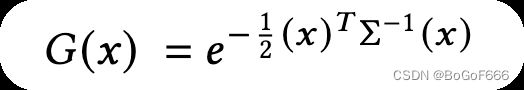
在blending混合过程中，这个高斯会被乘上 $\alpha$。
在渲染的时候我们需要将3D高斯投影到2D，这个过程使用此公式： ${\Sigma }^{\prime }=JW\Sigma W^T{J}^T$，其中W是视角转换(viewing transformation)矩阵， ${\Sigma }^{\prime }$是协方差矩阵， $J$是雅可比矩阵（Jacobian）即射影变换(projective transformation)的仿射近似（affine approximation），由于协方差矩阵需要保证半正定性(positive semi-definite)，所以没有办法直接优化，因此，我们使用了3D高斯的协方差矩阵 $\Sigma$ 类似于描述椭球的配置，给定一个缩放矩阵 S 和旋转矩阵 R，我们可以找到相应的 $\Sigma$： $\Sigma =RS{S}^T{R}^T$，为了允许对这两个因素进行独立优化，我们分别存储他们：用于缩放3D向量 $s$和表示旋转的四元素 $q$，为了避免训练过程中自动微分造成的显著开销，我们在实现中明确的推导出所有参数的梯度。

3.2 三维高斯自适应感知控制优化

本文的核心创新是优化步骤，它创建了一个密集的3D高斯点集，精准的表示场景以进行free-view synthesis。除了对3D位置 $p$、透明度 $\alpha$、协方差 $\Sigma$，我们还优化了每个高斯点颜色 $c$的SH系数，以正确捕捉场景的视点相关外观。

3.2.1 优化

优化是基于连续的迭代，先渲染，之后将生成的图像与捕捉数据集中的训练视图进行loss计算。不可避免的，由于3D到2D投影的模糊性，几何形状可能会被错误的放置。因此我们的优化需要能够创建geometry，如果geometry被错误地定位，也会remove或move geometry。3D高斯协方差参数的质量对于表示的紧凑性至关重要，因为可以用少量的large各向异性高斯捕获大的均匀的区域。优化器使用了SGD，透明度 $\alpha$使用的了sigmoid作为激活函数来将value限制在[0, 1)范围内，协方差的scale使用了exp激活函数来限制value范围。
我们将初始协方差矩阵估计为各向同性高斯，其轴等于到最近三个点的距离的平均值。我们使用类似于plenoxels的标准指数衰减调整（standard exponential decay scheduling）技术，但只适用于位置。损失函数包含了D-SSIM项： $\mathcal{L}=(1-\lambda ){\mathcal{L}}_1+\lambda {\mathcal{L}}_{\text{D-SSIM}}$，我们在所有的测试中都使用 $\lambda =0.2$。

3.2.2 高斯的自适应控制

我们从SfM的初始系数点集开始，然后应用我们的方法自适应的控制高斯的数量及其在单位体积1上的密度，允许我们从初始稀疏的高斯集到密集的集合，更好的表示场景，并具有正确的参数。在优化预热之后，我们每100次迭代就会触发稠密化，同时去除任何本质上透明的高斯点，即当该高斯点的 $\alpha$透明度低于某个阈值 ${ϵ}_{\alpha }$时。
我们对高斯的自适应控制需要填充空区域，它侧重于缺少几何特征的区域（“重建不足”），但在高斯覆盖场景中大面积的区域（通常对应于“重建过度”）。我们观察到两者都具有较大的视图空间位置梯度，直观的说，这可能是因为它们对应于尚未很好地重建的区域，并且优化试图移动高斯点来纠正这一点。
由于这两种情况都是稠密化比较好的候选区域，因此我们对平均幅度视图空间位置梯度高于阈值 ${\tau }_{pos}$的高斯进行稠密化，在实验中我们将这个阈值设置为0.0002。

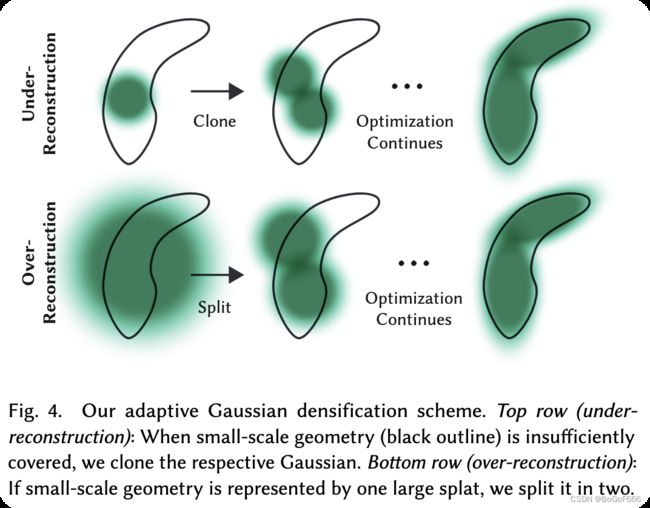
高斯自适应详细步骤（如上图）：

1. 对重构不足的区域的小高斯函数，我们需要覆盖必须创建的新geometry，为此，最好通过简单地创建相同大小的副本并将其移动到位置梯度的方向来克隆高斯。
2. 另外，高方差区域的大高斯函数需要被分成更小的高斯函数，我们用两个新的高斯替换这样的高斯点。并将它们的比例除以我们在实验中确定的系数 $\varphi =1.6$，我们还使用原始的3D高斯作为PDF进行采样来初始化他们的位置。

存在的问题：
在上述第一种情况下，我们通过增加高斯数来增加系统总体积，在第二种情况下，我们保持总体积但是增加高斯点数。但是我们的优化可能会被卡在靠近输入相机的漂浮物上（相机缺陷/烟雾），在实践中，这可能会导致高斯密度的不合理增加，一个有效的解决方法是：每迭代 $N=3000$次，就将 $\alpha$值设置为接近零，之后优化策略会对有效的高斯点提升 $\alpha$，同时无效的高斯点会被之前讲到的透明度阈值 ${ϵ}_{\alpha }$剔除。高斯可能会缩小或增长，并且与其他高斯有很大的重叠，但我们定期删除世界空间中非常大的高斯和视图空间中占用较大的高斯。这种策略总体上可以很好地控制高斯的总数。

用于高斯的快速可微栅格化器(Differentiable rasterizer)：
我们的目标是具有快速的整体渲染和快速排序，以允许alpha-blend——包括anisotropic splats——并避免先前工作中对可以存在的梯度的斜率数量的硬约束。为了实现这些目标，我们设计了一种基于tile的高斯溅射光栅化器，首先一次性对整个图像进行预排序，避免了对每个像素进行排序的成本，这阻碍了以前的alpha-blending解决方案。我们的快速光栅化器允许对任意数量的混合高斯进行有效的反向传播，这些混合高斯具有较低的额外内存消耗，每个像素只需要恒定的开销。我们的光栅化管线是完全可微的，并且给定到2D的投影可以栅格化类似于以前的2D溅射方式的各向异性(anisotropic)溅射。

我们的方法首先将屏幕分割成16x16个贴图，然后继续根据视锥和每个贴图对3D高斯进行剔除。具体来说，我们只保留与视锥相交的99%置信区间的高斯。此外，我们使用保护带来简单地拒绝极端位置的高斯（即，那些均值接近近平面且远离视锥体的高斯分布，因为计算它们的投影2D协方差将是不稳定的。然后我们根据高斯重叠tiles的数量初始化每个高斯并为每个instance分配一个结合了视图空间深度和tile ID的key。然后我们使用单个快速GPU Radix排序基于这些key对高斯进行排序。注意，没有额外的逐点排序，并且基于这个初始排序执行blending，因此，我们的alpha- blending可以在某些config中近似。然而，随着splats接近单个像素的大小，这些近似值变得可以忽略不计。我们发现这种选择大大提高了训练和渲染性能，而不会在收敛场景中产生可见的artifacts。

在对高斯进行排序之后，我们通过识别splat到给定tile的第一个和最后一个深度排序条目来为每个tile生成一个列表。对于光栅化，我们为每个tile启动一个线程块。每个块首先协作将高斯的数据包加载到共享内存中，然后对于给定的像素，通过从前到后遍历列表累积颜色和 $\alpha$透明度，从而最大化数据加载/共享和处理的并行增益。当我们在像素中达到目标饱和度 $\alpha$时，相应的线程停止。定期，查询tile中的线程，当所有像素饱和时，整个tile的处理终止（即 $\alpha =1$时）。

在光栅化过程中， $\alpha$的饱和是唯一的停止条件，与之前的工作相比，我们不限制接受梯度更新和混合primitives的数量，我们强制执行此方法以允许我们的算法可以处理具有任意、不同深度复杂性的场景并准确的学习它们，而无需求助于特定于场景的超参调整。因此，在反向传播期间，我们必须恢复前向传递中每个像素的混合点的完整序列。一种解决方案是在全局内存中存储任意长的混合点列表。为了避免隐含的动态内存管理开销，我们改为选择再次遍历每个tile列表，我们可以重用排序的高斯数组和tile的范围从前向传播。为了便于梯度计算，我们现在将从后到前遍历它们。

遍历从tile中的任何像素的最后一个点开始，并将点加载到共享内存中再次发生协作。此外，如果每个像素的深度小于或等于前向传递期间对颜色有贡献的最后一个点的深度，则每个像素只会开始（昂贵的）重叠测试和处理。梯度计算需要原始混合过程中每一步的积累不透明值。我们可以通过在前向传递结束时仅存储总累积不透明度来恢复这些中间不透明度，而不是通过遍历一系列显性的反向传递中逐渐缩小不透明度。具体来说，每个点在前向过程中存储最终的累积不透明度 $\alpha$。我们将其除以我们的前后遍历中的每个点的 $\alpha$，以获得梯度计算所需要的系数。

4. 实现和实验

实现

• 栅格化是使用cuda kernel实现的，使用了NVIDIA CUB排序routine进行快速基数排序（fast Radix sort）；
• 优化细节：为了稳定性，我们先以较低的分辨率进行warmup计算，具体来说，我们使用4倍的图像分辨率开始优化，我们在250和500次迭代之后两次上采样。
• SH系数优化对角度信息的缺乏很敏感，对于典型的类Nerf、在中心物体半球拍摄多视角图片的场景，优化效果很好。但是如果capture有角度区域缺失（如，当录制的场景的角落，或者执行“内部输出”捕获）可以通过优化产生SH零阶分量（即基色或漫反射）的完全不正确值。为了克服这个问题，我们首先只优化零阶分量，然后在每1000次迭代后引入SH的一个波段，知道表示SH的所有4个波段。
• 方法在13个真实场景上进行了测试，所有测试是在A6000 GPU上执行的。
• 本文使用PSNR、L-PIPS 和 SSIM 指标来计算error；
• 本文训练轮次存在两个setting：7k和30k。
  

实验

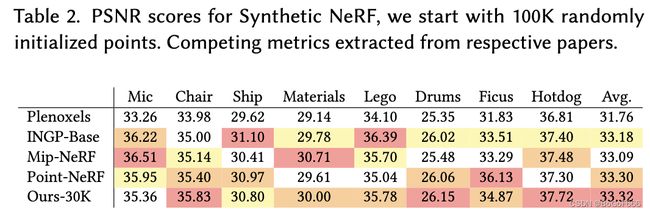
人工合成有界场景：除了真实场景之外，我们还在人工合成的blender数据集上评估我们的方法。即使随机初始化，我们也可以获得最先进的结果：我们从包含场景边界的体积内100k均匀随机高斯开始训练，我们的方法快速自动将它们修剪到大约6-10k有意义的高斯，30k次迭代后训练模型的最终大小每个场景达到大约200-500k高斯，我们使用白色背景来报告和比较我们获得的PSNR分数。

紧凑形式：对比之前的显式场景表示，我们优化中使用的各向异性高斯（anisotropic gaussian）能够在参数数量较少的同时建模复杂形状。对比之前的SOTA point-based方法，我们使用接近1/4之于原始点云的数量，获得相似的visual质量，平均模型大小3.8MB，对比它们的9MB。实验显示我们只使用了两度球谐函数。

消融实验

从SfM点进行初始化：我们评估了从SfM点云初始化3D高斯的重要性。对于这种消融，我们统一采用一个大小等于输入相机边界框三倍的立方体。我们观察到我们的方法表现相对较好，即使没有SfM点，也避免了完全失败。相反，它主要在背景（background）中退化（图7）。此外，在训练视图中没有很好的覆盖的区域，随机初始化方法似乎有更多的漂浮物，无法通过优化去除。另一方面，合成NeRF数据集没有这种行为，因为它没有背景并且受到输入相机的良好约束。

稠密化：我们还评估了两种稠密化的方法，具体的说，就是我们描述的克隆和拆分的策略，我们分别禁用两种方法，并使用其余方法进行优化比边，结果表明，分割大高斯对于允许很好地重建背景很重要，如图8，而克隆小高斯而不是拆分它们可以实现更好更快的收敛，尤其是当薄结构出现在场景中时。

具有梯度到溅射到无限深度复杂性：我们评估了如果跳过N个最前面的点之后的梯度计算将在不牺牲质量的情况下为我们提供加速，在测试中，我们设定N=10，这比在Pulsar中的默认值高两倍，但是由于梯度计算中的严重近似，他导致优化不稳定，对于卡车（Truck）场景，PSNR质量下降11dB，Garden场景的视觉效果：

各向异性协方差：我们的方法中的一个重要算法选择是优化3D高斯的完整协方差矩阵。为了证明这种选择的效果，我们进行了消融，我们通过优化单个标量值来消除各向异性，该值控制所有三个轴上3D高斯的半径。该优化结果如下图，我们观察到各向异性显著提高了三位高斯与曲面对齐能力的质量，这个反过来又允许更高的渲染质量，同时保持相同数量的点。
球面谐波（SH）：最后球面谐波的使用提高了我们的总体PSNR分数，因为他们补偿了视觉相关的效应。（见table3）

结论

局限性

• 尽管各向异性高斯具有很多优点，但是我们的方法可以创建拉长的伪影或者“斑点”高斯，同样以前的方法在这些情况下也会遇到困难。如下图：
  [图片]
• 当我们优化创建大高斯点时，我们偶尔会出现伪影出现，这往往会发生在与视图相关的外观的区域，这些弹出伪影的一个原因是在光栅化器中通过防护带（guard band）简单地剔除高斯。更有原则的剔除方法将减轻这些伪影。另一个因素是我们简单的可见性算法，这可能导致高斯突然切换深度/混合顺序，这可以通过抗锯齿来解决。
• 此外，我们目前没有将任何正则化应用于我们的优化，如果这样做可能有助于优化没见过的区域和弹出伪影的问题。
• 虽然我们使用相同的超参数进行完整的评估，但早期的实验表明，在非常大的场景（例如，城市数据集）中减少位置学习率是必要的。
• 在渲染场景时候的内存占用还是比较大，需要存储几百MB的训练好的场景模型以及30-500MB给到光栅化器，具体也需要考虑到场景size大小以及渲染图像的分辨率，所以未来需要考虑减少内存的占用，以及考虑如何将点云压缩技术和我们的高斯表征进行结合。