大厂Mysql高频面试题-!为什么-B,被面试官怼哭的Spring原理
也就是说,我们的需求增加了,我们希望数据的组织方式,既要有一定规则,又要有序。
在引出这种数据结构之前,我们首先来看一种查找方式:二分查找。
高效的查找方式:二分查找
二分查找的核心思想是给定一个有序的数组,在查找过程中采用跳跃式的方式查找,即先以有序数列的中点位置为比较对象,如果要查找的元素小于中点元素,则将待查序列缩小为左半部分,否则为右半部分。通过每次比较,将查找区间减少一半,直到找到所需元素。
比如要从以下序列中查找到数字4
[1,3,4,5,6,7,8]
需要经过下面的查找步骤:
-
取中心位置对应元素,显然5大于4,在左边区间[1,3,4]进行查找
-
继续取中心位置对应元素3,显然3大于4,在右边区间[4]进行查找
-
4等于4,所以我们查找成功。
可以看到二分查找的效率是O(log n)。
由于有序数组自身的有序性,所以范围查询依然可以通过二分查找的方式查找区间的边界来实现。
这样看来,如果单从查询效率上来说,有序的数组是一种很好的选择。
但是显然有序数组对于插入和删除并不友好,假设我们要插入元素或者删除元素,都需要把部分元素全部向后或者向前移动,最糟糕的时间复杂度是O(n)。
有没有这样一种数据结构,既有一定顺序,又方便插入和删除呢?事实上,基于二分查找的思想,诞生了这样一种数据结构:二分查找树。
基于二分查找思想的二叉查找树
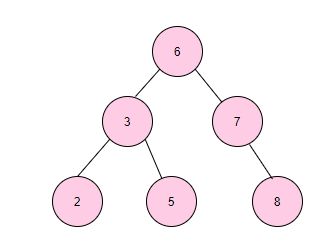
二叉查找树(Binary Search Tree)即BST树是这样的一种数据结构,如下图:
在二叉搜索树中:
1).若任意结点的左子树不空,则左子树上所有结点的值均不大于它的根结点的值。
2).若任意结点的右子树不空,则右子树上所有结点的值均不小于它的根结点的值。
3).任意结点的左、右子树也分别为二叉搜索树。
这样的结构非常适合用二分查找的思维查找元素。
比如我们需要查找键值为8的记录:
- 先从根找起,找到6;
- 显然8>6,所以接着找到6的右子树,找到7;
- 显然8>7, 所以找7的右子树,找到了8,查找结束。
这样一棵子树高度差不大于1的二叉查找树的查找效率接近与O(log n);
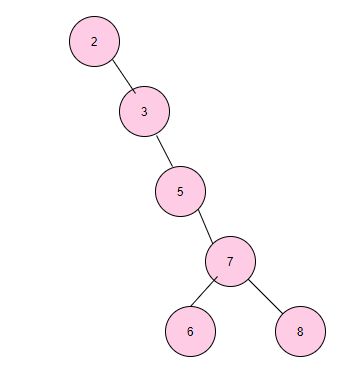
但是当二叉树的构造变成这样时,
此时我们再查找8时,查找效率就沦为接近顺序遍历查找的效率。
显然这不是我们想要的,二叉查找树也需要balance。
升级版的BST树:平衡二叉树
我们对二叉查找树做个限制,限制必须满足任何节点的两个子树的最大差为1,也是平衡二叉树的定义,这样我们的查找效率就有了一定的保障。
平衡二叉树(self-balancing binary search tree),又叫AVL树。
当然,维护平衡二叉树也是需要一定开销的,即当树插入/更新/删除新的数据时假设破坏了树的平衡性,那么需要通过左旋和右旋来维护树的平衡。
当数据量很多时,同样也会出现二叉树过高的情况。
我们知道平衡二叉树的查找效率为 O(log n),也就是说,当树过高时,查找效率会下降。
另外由于我们的索引文件并不小,所以是存储在磁盘上的。
文件系统需要从磁盘读取数据时,一般以页为单位进行读取,假设一个页内的数据过少, 那么操作系统就需要读取更多的页,涉及磁盘随机I/O访问的次数就更多。
将数据从磁盘读入内存涉及随机I/O的访问,是数据库里面成本最高的操作之一。
因而这种树高会随数据量增多急剧增加,每次更新数据又需要通过左旋和右旋维护平衡的二叉树,不太适合用于存储在磁盘上的索引文件。
更加符合磁盘特征的B树
前面我们看到,虽然平衡二叉树既有链表的快速插入与删除操作的特点,又有数组快速查找的优势,但是这并不是最符合磁盘读写特征的数据结构。
也就是说,我们要找到这样一种数据结构,能够有效的控制树高,那么我们把二叉树变成m叉树,也就是下图的这种数据结构:B树。
B树是一种这样的数据结构:
1.根结点至少有两个子结点;
2.每个中间节点都包含k-1个元素和k个子结点,其中 m/2 <= k <= m;
3.每一个叶子结点都包含k-1个元素,其中 m/2 <= k <= m;
4.所有的叶子结点都位于同一层;
5.每个结点中关键字从小到大排列,并且当该结点的孩子是非叶子结点时,该k-1个元素正好是k个子结点包含的元素的值域的分划。
可以看到,B树在保留二叉树预划分范围从而提升查询效率的思想的前提下,做了以下优化:
二叉树变成m叉树,这个m的大小可以根据单个页的大小做对应调整,从而使得一个页可以存储更多的数据,从磁盘中读取一个页可以读到的数据就更多,随机IO次数变少,大大提升效率。
但是我们看到,我们只能通过中序遍历查询全表,当进行范围查询时,可能会需要中序回溯。
不断优化的B树:B+树
基于以上的缺陷,又诞生了一种新的优化B树的树:B+树
B+树在B树的基础上加了以下优化:
1.叶子结点增加了指针进行连接,即叶子结点间形成了链表;
2.非叶子结点只存关键字key,不再存储数据,只在叶子结点存储数据;
说明:叶子之间用双向链表连接比单向链表连接多出的好处是通过链表中任一结点都可以通过往前或者往后遍历找到链表中指定的其他结点。
这样做的好处是:
1.范围查询时可以通过访问叶子节点的链表进行有序遍历,而不再需要中序回溯访问结点。
总结
无论是哪家公司,都很重视高并发高可用的技术,重视基础,重视JVM。面试是一个双向选择的过程,不要抱着畏惧的心态去面试,不利于自己的发挥。同时看中的应该不止薪资,还要看你是不是真的喜欢这家公司,是不是能真的得到锻炼。其实我写了这么多,只是我自己的总结,并不一定适用于所有人,相信经过一些面试,大家都会有这些感触。
最后,如果有想要我整理的面试资料的,可以**戳这里免费领取**,我整理了一些面试真题资料,技术知识点剖析教程,还有和广大同仁一起交流学习共同进步,还有一些职业经验的分享。
![]()
取](https://gitee.com/vip204888/java-p7)**,我整理了一些面试真题资料,技术知识点剖析教程,还有和广大同仁一起交流学习共同进步,还有一些职业经验的分享。
[外链图片转存中…(img-9sMAeb0Y-1628619515186)]