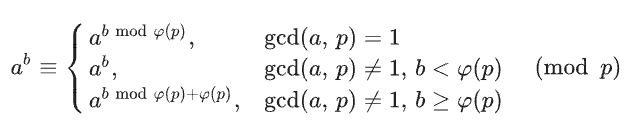牛客竞赛数学专题班同余与模 题解
【模板】同余方程
模板题,直接用exgcd就行了,上一场的青蛙的约会搞懂了,自然就会了。
#include 【模板】乘法逆元
方法1:线性求逆元,详细方式推导可以参考oi-wiki https://oi-wiki.org/math/number-theory/inverse/#_5
#include 方法2:因为 n n n的数据范围比较大,所以不能用费马小定理+快速幂硬求,考虑如何减少用快速幂求逆元的次数。
对于数组 a 1 , a 2 , a 3 , a 4 a_1,a_2,a_3,a_4 a1,a2,a3,a4,若要求 a 2 a_2 a2的逆元,只需要求 a 2 − 1 = ( a 1 a 2 a 3 a 4 ) − 1 ⋅ ( a 1 a 3 a 4 ) a_2^{-1}=(a_1a_2a_3a_4)^{-1}\cdot (a_1a_3a_4) a2−1=(a1a2a3a4)−1⋅(a1a3a4),记录一个前缀和一个后缀就行了。(当时写的时候并不会线性求逆元)
#include Alternating Sum
由上图可知,可以将求和式 ∑ i = 0 n s i a n − i b i \sum_{i=0}^ns_ia^{n-i}b^i ∑i=0nsian−ibi分成 c n t = ( n + 1 ) / k cnt=(n+1)/k cnt=(n+1)/k个小段,每一段内的求和值为 t [ i ] = t [ i − 1 ] × a − k b k , t [ 1 ] = ∑ i = 0 k − 1 s i a n − i b i t[i]=t[i-1]\times a^{-k}b^k,t[1]=\sum_{i=0}^{k-1}s_ia^{n-i}b^i t[i]=t[i−1]×a−kbk,t[1]=∑i=0k−1sian−ibi,可以用等比数列前 n n n项和的公式求出,公比为 a − k b k a^{-k}b^k a−kbk。
注意:当公比为1时,不能用等比数列前 n n n项和来计算,需要特判。
对于最后剩下的长度不足 k k k的一段,可以直接暴力求解。
#include 扩展中国剩余定理
直接套excrt的板子。
#include Biorhythms
当三重峰值出现时,一定满足 x = p + 23 t 1 = e + 28 t 2 = i + 33 t 3 x=p+23t_1=e+28t_2=i+33t_3 x=p+23t1=e+28t2=i+33t3,可以列出同余方程为
{ x ≡ p ( m o d 23 ) x ≡ e ( m o d 28 ) x ≡ i ( m o d 33 ) \left\{\begin{matrix} x\equiv p(\mod 23) \\ x\equiv e(\mod 28) \\ x\equiv i(\mod 33) \end{matrix}\right. ⎩⎨⎧x≡p(mod23)x≡e(mod28)x≡i(mod33)
直接套excrt,求出通解。
注意题目要求的是从日期d到下一个三重峰的天数,要求出特解。
#include Notepad
欧拉降幂裸题。
所有 n n n位 b b b进制的数有 b n b^n bn个,含前导 0 0 0的数有 b n − 1 b^{n-1} bn−1个,总共需要记录的数有 b n − b n − 1 = ( b − 1 ) b n − 1 b^n-b^{n-1}=(b-1)b^{n-1} bn−bn−1=(b−1)bn−1个,直接对 c c c取模。
当取模结果为 0 0 0时,最后一页记录的数字是 c c c个,需要特判一下。
#include Power Tower
m → φ ( m ) → φ ( φ ( m ) ) → . . . → 1 m\rightarrow \varphi(m) \rightarrow \varphi(\varphi(m)) \rightarrow...\rightarrow1 m→φ(m)→φ(φ(m))→...→1 ,这个步骤最多会进行 log m \log m logm次。
对于每次的查询区间 [ l , r ] [l,r] [l,r],最多计算 log m \log m logm次,总的复杂度就是 O ( q log m ) O(q\log m) O(qlogm)。
计算幂的时候要用到欧拉降幂。
#include GCD Table
若选中的起始位置为 ( i , j ) (i,j) (i,j),则:
{ g c d ( i , j ) ) = a 1 g c d ( i , j + 1 ) ) = a 2 g c d ( i , j + 2 ) ) = a 3 ⇔ { j ≡ 0 ( m o d a 1 ) j ≡ − 1 ( m o d a 2 ) j ≡ − 2 ( m o d a 3 ) \begin{matrix} \left\{\begin{matrix} gcd(i,j)) &=& a_1 \\ gcd(i,j+1)) &=& a_2 \\ gcd(i,j+2)) &=& a_3 \end{matrix}\right. & \Leftrightarrow & \left\{\begin{matrix} j &\equiv& 0(\mod a_1) \\ j &\equiv& -1 (\mod a_2) \\ j &\equiv& -2 (\mod a_3) \end{matrix}\right. \end{matrix} ⎩⎨⎧gcd(i,j))gcd(i,j+1))gcd(i,j+2))===a1a2a3⇔⎩⎨⎧jjj≡≡≡0(moda1)−1(moda2)−2(moda3)
上式可以通过excrt求得 j j j的通解: j = j 0 + M ⋅ x , M = l c m ( a 1 , a 2 . . . a k ) j=j_0+M\cdot x,\ M=lcm(a_1,a_2...a_k) j=j0+M⋅x, M=lcm(a1,a2...ak),且 i i i是 M M M的倍数, i = M + M ⋅ y i=M+M\cdot y i=M+M⋅y。
若 g = g c d ( M , j 0 ) g=gcd(M,j_0) g=gcd(M,j0), g ′ = g c d ( M + M ⋅ y , j 0 + M ⋅ x ) g'=gcd(M+M\cdot y,j_0+M\cdot x) g′=gcd(M+M⋅y,j0+M⋅x),可以看出 g ∣ g ′ g|g' g∣g′。
只需要判断 j = j 0 , i = M j=j_0,i=M j=j0,i=M是否成立就行了,因为 g c d ( i , j + t ) gcd(i,j+t) gcd(i,j+t)有可能是 a t + 1 a_{t+1} at+1的倍数,这样条件就不成立。
#include