C语言数据结构-实验
数据结构实验
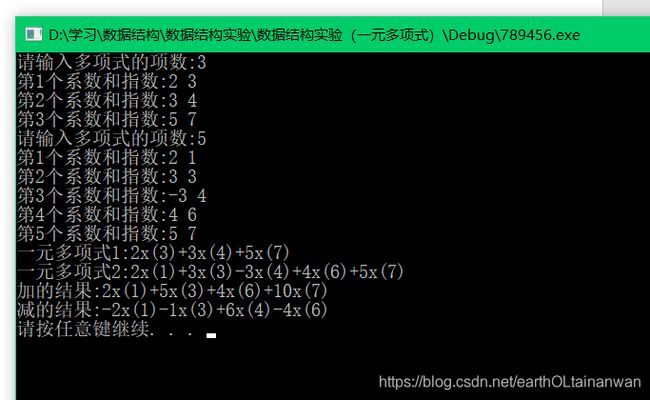
- 一元多项式
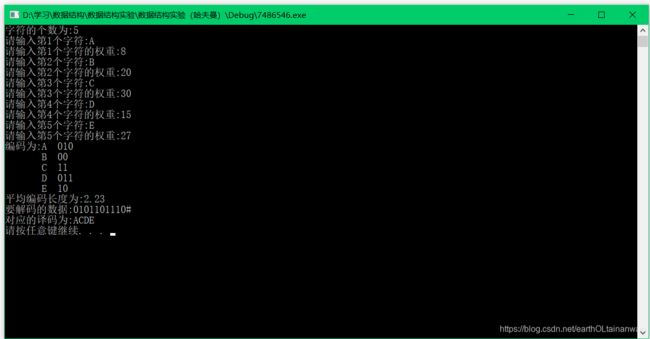
- 哈夫曼编码和译码
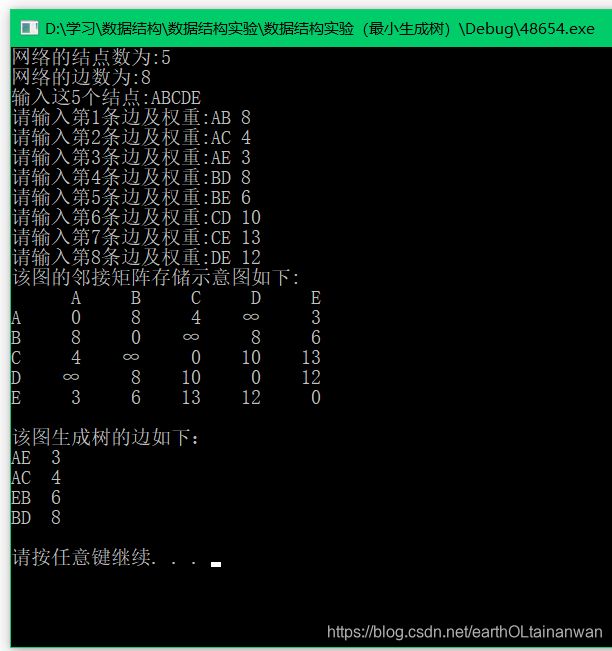
- 求图的最小生成树
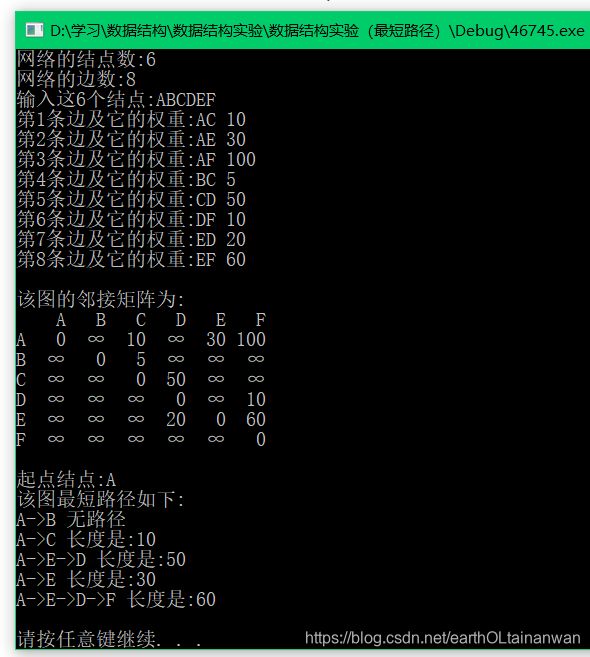
- 最短路径
- 快速排序
具体是根据老师给的实验要求,其中部分代码由老师给出
一元多项式
#include 哈夫曼编码和译码
#include 求图的最小生成树
#include 最短路径
#include快速排序
#include