redis跳跃表源码详解

前言

跳跃表是一种有序的数据结构，他通过在每个节点中维护多个指向其它节点的指针，从而达到快速访问节点的目的。跳跃表的查找操作平均时间复杂度为o(logN)。在大部分情况下，跳跃表的效率和平衡二叉树相当，且跳跃表的实现更为简单。redis中有序集合的底层实现就是使用了跳跃表。

相关数据结构

/* ZSETs use a specialized version of Skiplists */
typedef struct zskiplistNode {
    sds ele;
    double score;
    struct zskiplistNode *backward;
    struct zskiplistLevel {
        struct zskiplistNode *forward;
        unsigned int span;
    } level[];
} zskiplistNode;

typedef struct zskiplist {
    struct zskiplistNode *header, *tail;
    unsigned long length;
    int level;
} zskiplist;

其中主要涉及到两个数据结构zskiplist和zskiplistNode。下图是一个典型的跳跃表结构

图1, 跳跃表结构

zskiplist结构
最左侧的样例就是一个。其中header指向头结点。tail指向为节点，level等于5，表示该跳跃表中所有结点的最高层数为5(注意，不包括头结点)，length等于3，表示该跳跃表结点个数为3个(同样不包含头结点)。

zskiplistNode结构
zskiplistLevel，表示“层” 图1中L1,L2…都是一个skiplistLevel结构。该结构包含一个前向指针foward, 一个和forward结点的跨度span.

backward 表示该结点的后向结点。如果希望从后往前遍历整个跳跃表，该结点就相当好使了。

score 分直，各结点排序的重要参考

obj 成员对象

【文章福利】需要C/C++ Linux服务器架构师学习资料加群812855908（资料包括C/C++，Linux，golang技术，Nginx，ZeroMQ，MySQL，Redis，fastdfs，MongoDB，ZK，流媒体，CDN，P2P，K8S，Docker，TCP/IP，协程，DPDK，ffmpeg等）

相关API

跳跃表除了寻常的创建(zslCreate)，插入(zslInsert),查找(zslGetRank), 删除(aslDelete)之外，还包括范围查找，范围删除等批量操作。

/* Create a new skiplist. */
zskiplist *zslCreate(void) {
    int j;
    zskiplist *zsl;

    zsl = zmalloc(sizeof(*zsl));
    zsl->level = 1;
    zsl->length = 0;
    zsl->header = zslCreateNode(ZSKIPLIST_MAXLEVEL,0,NULL);//ZSKIPLIST_MAXLEVEL=32
    for (j = 0; j < ZSKIPLIST_MAXLEVEL; j++) {
        zsl->header->level[j].forward = NULL;
        zsl->header->level[j].span = 0;
    }
    zsl->header->backward = NULL;
    zsl->tail = NULL;
    return zsl;
}

/* Create a skiplist node with the specified number of levels.
 * The SDS string 'ele' is referenced by the node after the call. */
zskiplistNode *zslCreateNode(int level, double score, sds ele) {
    zskiplistNode *zn =
        zmalloc(sizeof(*zn)+level*sizeof(struct zskiplistLevel));
    zn->score = score;
    zn->ele = ele;
    return zn;
}

zslCreate
创建一个zskiplist 结构，以及一个头结点。这里应该很好理解。不多介绍。

/* Insert a new node in the skiplist. Assumes the element does not already
 * exist (up to the caller to enforce that). The skiplist takes ownership
 * of the passed SDS string 'ele'. */
zskiplistNode *zslInsert(zskiplist *zsl, double score, sds ele) {
    zskiplistNode *update[ZSKIPLIST_MAXLEVEL], *x;
    unsigned int rank[ZSKIPLIST_MAXLEVEL];
    int i, level;

    serverAssert(!isnan(score));
    x = zsl->header;
    for (i = zsl->level-1; i >= 0; i--) {
        /* store rank that is crossed to reach the insert position */
        rank[i] = i == (zsl->level-1) ? 0 : rank[i+1];
        while (x->level[i].forward &&
                (x->level[i].forward->score < score ||
                    (x->level[i].forward->score == score &&
                    sdscmp(x->level[i].forward->ele,ele) < 0)))
        {
            rank[i] += x->level[i].span;
            x = x->level[i].forward;
        }
        update[i] = x;
    }
    /* we assume the element is not already inside, since we allow duplicated
     * scores, reinserting the same element should never happen since the
     * caller of zslInsert() should test in the hash table if the element is
     * already inside or not. */
    level = zslRandomLevel();
    if (level > zsl->level) {    //新节点的level比所有的其它的节点level都高
        for (i = zsl->level; i < level; i++) {
            rank[i] = 0;//rank[i]是update[i]指向的节点的排位，level和zsl->level之间的层是没有指向的，未初始化的，所以rank为0
            update[i] = zsl->header;
            update[i]->level[i].span = zsl->length;
        }
        zsl->level = level;
    }
    x = zslCreateNode(level,score,ele);
    for (i = 0; i < level; i++) {
        /*链式更新，和链表插入操作类似。因为插入新的节点所以forward指针(类似next指针)要变动*/
        x->level[i].forward = update[i]->level[i].forward;
        update[i]->level[i].forward = x;

        /* update span covered by update[i] as x is inserted here */
        /*
rank[0]表示的是update[0]指向的节点的排位，该节点肯定是新插入节点的后向节点*/
        /*rank[i]表示的是update[i]指向的节点的排位，该节点的前向节点的level[i]指向的就是新节点*/
        /*rank[0]-rank[i] 就是排位之差。插入新节点前update[i]->level[i].span是其和update[i]->level[i]->forward之间的排位差*/
        /*那么可知update[i]->level[i]->forward的排位应该是rank[i]+update[i]->level[i].span,当插入了新节点，将变成update[i]->level[i] ->x(新节点)->update[i]->level[i]->forward,*/
        /*update[i]->level[i]->forward的排位将变成rank[i]+update[i]->level[i].span+1 == rank[0]+1+x->level[i].span*/
        /*所以可知x->level[i].span = update[i]->level[i].span - (rank[0] - rank[i])*/
        
        x->level[i].span = update[i]->level[i].span - (rank[0] - rank[i]);
        update[i]->level[i].span = (rank[0] - rank[i]) + 1;
    }

    /* increment span for untouched levels */
    for (i = level; i < zsl->level; i++) {
        update[i]->level[i].span++;
    }

    x->backward = (update[0] == zsl->header) ? NULL : update[0];
    if (x->level[0].forward)
        x->level[0].forward->backward = x;
    else
        zsl->tail = x;
    zsl->length++;
    return x;
}

int zslRandomLevel(void) {
    int level = 1;
    while ((random()&0xFFFF) < (ZSKIPLIST_P * 0xFFFF))
        level += 1;
    return (level<ZSKIPLIST_MAXLEVEL) ? level : ZSKIPLIST_MAXLEVEL;
}

zslInsert
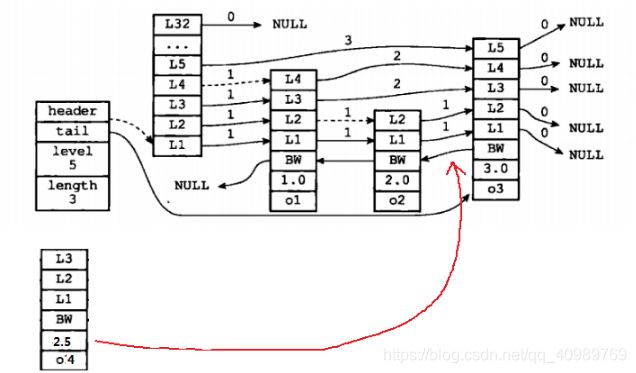
zslInsert相对来说复杂点。可以看到在这个函数中使用了update指针数组和rank数组，他们的大小都是ZSKIPLIST_MAXLEVEL=32. 其中update[i]指向的是第i层最接近所要插入点的那个结点。

图2，插入示例

如图2所示，我们现在要插入一个结点，score为2.5。我们知道应该是插入到o2和o3之间。在这个示例中update[0]指向的是o2, update[1]也指向o2, update[2]和update[3]指向o1, update[4]-updatep[31]指向的是头结点。而rank[i]则表示的是update[i]指向的节点的排位，或者说是与头结点的间距。如上例中，rank[0]表示与update[0]指向的节点也就是o2的排位，故rank[0]=2，rank[1]=2, rank[2]=rank[3]=1.

在插入一个node的时候，层高是随机的可以看zslRandomLevel这个函数，level是1~32之间的一个数值。如上例子中，我们新插入的节点，level=3。当插入一个节点的时候，必不可少的是foward指针和backward指针的调整。参见代码中的
x->level[i].forward = update[i]->level[i].forward;

update[i]->level[i].forward = x;

这两行。稍微麻烦点的是进行span的计算与更新。在在代码中注释了，这里再啰嗦一下：

rank[0]表示的是update[0]指向的节点的排位，该节点肯定是新插入节点的后向节点

rank[i]表示的是update[i]指向的节点的排位，该节点的level[i]的前向节点指向的就是新节点

插入新节点前update[i]->level[i].span是其和update[i]->level[i]->forward之间的排位差

那么可知update[i]->level[i]->forward的排位应该是rank[i]+update[i]->level[i].span,

当插入了新节点，将变成update[i]->level[i] ->x(新节点)->update[i]->level[i]->forward

update[i]->level[i]->forward的排位将变成rank[i]+update[i]->level[i].span+1 == rank[0]+1+x->level[i].span

所以可知x->level[i].span = update[i]->level[i].span - (rank[0] - rank[i])

插入新节点后update[i]->level[i]->forward直接指向新节点x, 所以

update[i]->level[i].span= rank[0] - rank[i] +1 应该是很好理解的了。

后面部分的代码，应该就比较好理解了。整个zslInsert函数就是这么多内容了。

zslDelete
通过给定的obj 和 core 删除跳跃表中的节点。

/* Delete an element with matching score/element from the skiplist.
 * The function returns 1 if the node was found and deleted, otherwise
 * 0 is returned.
 *
 * If 'node' is NULL the deleted node is freed by zslFreeNode(), otherwise
 * it is not freed (but just unlinked) and *node is set to the node pointer,
 * so that it is possible for the caller to reuse the node (including the
 * referenced SDS string at node->ele). */
int zslDelete(zskiplist *zsl, double score, sds ele, zskiplistNode **node) {
    zskiplistNode *update[ZSKIPLIST_MAXLEVEL], *x;
    int i;

    x = zsl->header;
    for (i = zsl->level-1; i >= 0; i--) {
        while (x->level[i].forward &&
                (x->level[i].forward->score < score ||
                    (x->level[i].forward->score == score &&
                     sdscmp(x->level[i].forward->ele,ele) < 0)))
        {
            x = x->level[i].forward;
        }
        update[i] = x;
    }
    /* We may have multiple elements with the same score, what we need
     * is to find the element with both the right score and object. */
    x = x->level[0].forward;
    if (x && score == x->score && sdscmp(x->ele,ele) == 0) {
        zslDeleteNode(zsl, x, update);
        if (!node)
            zslFreeNode(x);
        else
            *node = x;
        return 1;
    }
    return 0; /* not found */
}

/* Internal function used by zslDelete, zslDeleteByScore and zslDeleteByRank */
void zslDeleteNode(zskiplist *zsl, zskiplistNode *x, zskiplistNode **update) {
    int i;
    for (i = 0; i < zsl->level; i++) {
        if (update[i]->level[i].forward == x) {
            /*update[i]->level[i]------span1--->x----span2----->x->level[i]->forward*/
            update[i]->level[i].span += x->level[i].span - 1;//更新span
            update[i]->level[i].forward = x->level[i].forward;//更新前向节点
        } else {
            update[i]->level[i].span -= 1;
        }
    }
    if (x->level[0].forward) {
        x->level[0].forward->backward = x->backward;
    } else {
        zsl->tail = x->backward;
    }
    while(zsl->level > 1 && zsl->header->level[zsl->level-1].forward == NULL)
        zsl->level--;
    zsl->length--;
}

for while嵌套的循环和zslInsert其实是一样的。找到与要删除节点有指向关系的节点。其实要找到删除的节点，只需要i=0的for循环就可以找到了。一直zsl->header->level[0]->forward…level[0]->forward就能找到。而update[i]之所以要找这么全，是因为update[i]与要删除的节点有指向关系，删除节点后，这些与之有关联的节点都需要更新。找到节点之后，调用zslDeleteNode函数。zslDeleteNode其实也挺简单的

1，更新与要删除节点x有指向关系的节点的span 与 foward

2， 调整后向节点，可能的话也变更tail节点

3，调整zskiplist的level

4，zskiplist的length -1;

zslGetRank
通过score和ele得到该节点在zskiplist中的排位

/* Find the rank for an element by both score and key.
 * Returns 0 when the element cannot be found, rank otherwise.
 * Note that the rank is 1-based due to the span of zsl->header to the
 * first element. */
unsigned long zslGetRank(zskiplist *zsl, double score, sds ele) {
    zskiplistNode *x;
    unsigned long rank = 0;
    int i;

    x = zsl->header;
    for (i = zsl->level-1; i >= 0; i--) {
        while (x->level[i].forward &&
            (x->level[i].forward->score < score ||
                (x->level[i].forward->score == score &&
                sdscmp(x->level[i].forward->ele,ele) <= 0))) {
            rank += x->level[i].span;
            x = x->level[i].forward;
        }

        /* x might be equal to zsl->header, so test if obj is non-NULL */
        if (x->ele && sdscmp(x->ele,ele) == 0) {
            return rank;
        }
    }
    return 0;
}

szlGetRank我觉得还是有点意思的，前面也说过，要得到某个节点的排位，最笨的方式就是zsl->header->level[0]->forward …level[0]->forward一直这样往前查找。当然，也可以通过zsl->tail->backward…backward从后往前找，然后结合zsl->lenght，也能得到。但是这种方式的查找时间复杂度为o(N), 上例代码是一种更快速的方式。每次

x = x->level[i].forward;

可能就有好几个跨度。

zslGetElementByRank

/* Finds an element by its rank. The rank argument needs to be 1-based. */
zskiplistNode* zslGetElementByRank(zskiplist *zsl, unsigned long rank) {
    zskiplistNode *x;
    unsigned long traversed = 0;
    int i;

    x = zsl->header;
    for (i = zsl->level-1; i >= 0; i--) {
        while (x->level[i].forward && (traversed + x->level[i].span) <= rank)
        {
            traversed += x->level[i].span;
            x = x->level[i].forward;
        }
        if (traversed == rank) {
            return x;
        }
    }
    return NULL;
}

这段代码其实和上面的zslGetRank挺像的，也是大跨步向前走。

zslDeleteRangeByRank

/* Delete all the elements with rank between start and end from the skiplist.
 * Start and end are inclusive. Note that start and end need to be 1-based */
unsigned long zslDeleteRangeByRank(zskiplist *zsl, unsigned int start, unsigned int end, dict *dict) {
    zskiplistNode *update[ZSKIPLIST_MAXLEVEL], *x;
    unsigned long traversed = 0, removed = 0;
    int i;

    x = zsl->header;
    for (i = zsl->level-1; i >= 0; i--) {
        while (x->level[i].forward && (traversed + x->level[i].span) < start) {
            traversed += x->level[i].span;
            x = x->level[i].forward;
        }
        update[i] = x;
    }

    traversed++;
    x = x->level[0].forward;
    while (x && traversed <= end) {
        zskiplistNode *next = x->level[0].forward;
        zslDeleteNode(zsl,x,update);
        dictDelete(dict,x->ele);
        zslFreeNode(x);
        removed++;
        traversed++;
        x = next;
    }
    return removed;
}

zslDeleteRangeByRank相当于结合复用了zslDelete和zslGetRank的功能。这里update[i]表示第i层排名最靠近 start的那个点。

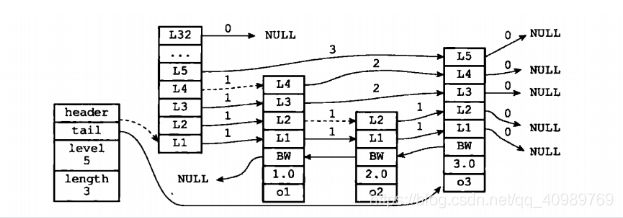
图3 跳跃表实例

我们依然引用图1 那幅图，为了便于观看，复制过来命名为图3. 比如我们想要删除的start为2，end为3.那么此时

update[0],update[1]应该指向的是o1节点，update[2],update[3]也指向的是o1节点， 而update[4]则是zsl->head.

然后挨个挨个删掉节点。

结尾

本文章跳跃表的源码来源于redis4.0.11中的t_zset.c。此处只介绍了几个关键的操作，其它比如还有zslInRange, zslFisrtInrang,zslDeleteRangeByScore等函数实现此处没有细讲。他们要么比较简单易懂，要么就有类似的实现了。

关注公众号，分享更多你感兴趣的互联网技术内容！