第一部分 表格型求解方法: 第二章 多臂赌博机
文章目录
- 第二章 多臂赌博机
-
- 2.1 一个k臂赌博机问题
- 2.2 动作-价值方法
- 2.3 10臂测试平台
-
- 课后练习
- 2.4 增量式实现
- 2.5 跟踪一个非平稳问题
-
- 练习题
- 2.6 乐观初始值
-
- 练习
- 2.7 基于置信度上界的动作选择
-
- 练习
-
- 官方答案:
- 2.8 梯度赌博机算法
-
- 练习
-
- 官方答案
- 通过随机梯度上升实现梯度赌博机算法
- 2.9 关联搜索(上下文相关的赌博机)
-
- 练习
- 2.10 本章小结
-
- 练习
第一部分表格型求解方法主要介绍
简单强化学习所使用的算法的核心思想,这种问题可以找到最优价值函数和最优策略。在其他部分,将会介绍只能找到 近似解的复杂(较大规模的动作和状态空间)强化学习问题
第二章 多臂赌博机
2.1 一个k臂赌博机问题
强化学习与其他机器学习方法不同的一点就在于,前者的训练信号是用来评估给定动作的好坏的,而不是通过给出正确动作范例来进行直接的指导。
多臂赌博机只有一个状态(非关联性),属于一种非关联性的评估性反馈问题,适合作为一个简化的问题来介绍强化学习,之后会之间探讨完整的强化学习问题。
k臂赌博机有k个控制杆,动作选择就是是否拉动控制杆,收益就是得到的奖金。
在k个动作中,每一个被选择时都对应一个期望收益或者平均收益,我们称为这个动作的价值。
q ∗ ( a ) = E [ R t ∣ A t = a ] q_*(a)=\mathbb{E}[R_t|A_t=a] q∗(a)=E[Rt∣At=a]
其中 q ∗ ( a ) q_*(a) q∗(a)代表在时间t采取a动作的价值,它等于期望收益。
我们将对动作a在时刻t时的价值估计记作 Q t ( a ) Q_t(a) Qt(a),我们希望它接近 q ∗ ( a ) q_*(a) q∗(a)。
在动作空间中,你都可以估计出每一个动作的价值,如果你总是选择估值最高的那个(或那些)动作,那这个动作称为贪心动作,这个对应概念开发(exploitation),如果你选择非贪心的动作,对应概念试探(exploration)。
“开发”对于当前时刻的利益最大化是正确的作法,但是“试探”长远来看可能带来总体收益的最大化。比如,假设一个贪心动作的价值是确切知道的,而另外几个动作的估计价值与之差不多,但是有很大的不确定性。这种不确定性足够使得至少一个动作实际上会好于贪心动作,但是你不知道是哪个。如果你还有很多时刻可以用来做选择,那么对非贪心的动作进行试探并且发现哪一个动作好于贪心动作也许会更好。在试探的过程中短期内收益较低,但从长远来看收益更高,因为你在发现了更好的动作后,你可以很多次地利用它。值得一提的是,在同一次动作选择中,开发和试探是不可能同时进行的,这种情况就是我们常常提到的开发和试探之间的冲突。
在一个具体案例中,到底选择“试探”还是“开发”,依赖于我们得到的函数估计、不确定性和剩余时刻的精确数值。
2.2 动作-价值方法
将使用价值的估计来进行动作选择的方法统称为动作-价值方法。
Q t ( a ) ≐ t 时 刻 前 通 过 执 行 动 作 a 得 到 的 收 益 总 和 t 时 刻 前 执 行 动 作 a 的 次 数 = ∑ i = 1 t − 1 R i ⋅ 1 A i = a ∑ i = 1 t − 1 1 A i = a Q_t(a) \doteq \frac{t时刻前通过执行动作a得到的收益总和}{t时刻前执行动作a的次数}=\frac{\sum_{i=1}^{t-1}R_i \cdot \mathbb{1}_{A_i=a}}{\sum_{i=1}^{t-1}\mathbb{1}_{A_i=a}} Qt(a)≐t时刻前执行动作a的次数t时刻前通过执行动作a得到的收益总和=∑i=1t−11Ai=a∑i=1t−1Ri⋅1Ai=a
其中, 1 p r e d i c a t e \mathbb{1}_{predicate} 1predicate表示随机变量,当predicate为真时其值为1,反之则为0。当分母为0时,将 Q t ( a ) Q_t(a) Qt(a)定义为一个默认值,比如 Q t ( a ) = 0 Q_t(a)=0 Qt(a)=0,当分母去西趋向无穷大,根据大数定律, Q t ( a ) Q_t(a) Qt(a)会收敛到 q ∗ ( a ) q_*(a) q∗(a),我们把这种估计动作价值的方法称为采样平均方法,因为每一次估计都是对相关样本的平均。
如果要选择贪心动作:
A t ≐ a r g m a x a Q t ( a ) A_t \doteq \underset{a}{argmax}Q_t(a) At≐aargmaxQt(a)
贪心策略的一个简单替代策略是:大部分时间都表现得贪心,但偶尔(比如以一个很小的概率 ϵ \epsilon ϵ)以一个独立于动作-价值估计值的方式从所有动作中等概率随机地做出选择。正文中近乎贪心的选择规则称为 ϵ \epsilon ϵ-贪心方法。
2.3 10臂测试平台
为了评估贪心方法和 ϵ \epsilon ϵ-贪心方法,将它们在一系列测试问题上进行比较。k=10,动作的真实价值为 q ∗ ( a ) , a = 1 , . . . , 10 q_*(a),a=1,...,10 q∗(a),a=1,...,10,从一个均值为0方差为1的标准正态(高斯)分布中选择。当对应于该问题的学习方法在时刻t选择 A t A_t At时,实际的收益 R t R_t Rt则由一个均值为 q ∗ ( A t ) q_*(A_t) q∗(At),方差为1的正态分布决定。如图2.1所示:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ThmfKXiZ-1636945189241)(D:\研究僧\RL\pic\fig2_1.jpg)]
图2.2比较了两种方法。它们都采用采样平均策略来形成对动作价值的估计。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-fcsCzaOy-1636945189244)(D:\研究僧\RL\pic\fig2_2.jpg)]
上部的图显示了期望的收益随着经验的增长而增长。贪心方法再最初增长得略微快一些,但是随后稳定在一个较低的水平。 ϵ \epsilon ϵ-贪心方法最终表现更好,因为他们持续地试探。 ϵ = 0.1 \epsilon=0.1 ϵ=0.1时方法试探地更多,通常更早发现最优动作,但是由于它“试探”的策略更多,它选择这个最优动作的概率永远不会超过 91 % ( 9 10 + 1 10 × 1 10 ) 91\% (\frac{9}{10}+\frac{1}{10}\times \frac{1}{10}) 91%(109+101×101), ϵ = 0.01 \epsilon=0.01 ϵ=0.01改善得更慢,但最终来看,它在两个测度(平均收益和最优动作概率)的表现最好。
ϵ \epsilon ϵ-贪心方法相对于贪心犯法的优势是依赖于任务的。
- 收益函数估计噪音越多, ϵ \epsilon ϵ-贪心方法比贪心方法好
- 问题非平稳时,即真实价值不是静态的,而是随着时间变化的, ϵ \epsilon ϵ-贪心方法也更优越
- 即使是确定性问题,以防万一, ϵ \epsilon ϵ-贪心方法也更好
课后练习
- 赌博机例子
k=4,记作1,2,3,4.使用 ϵ \epsilon ϵ-贪心方法进行动作选择,基于采样平均的动作价值估计,初始估计 Q 1 ( a ) = 0 , ∀ a Q_1(a)=0,\forall a Q1(a)=0,∀a。假设动作及最初顺序是 A 1 = 1 , R 1 = − 1 , A 2 = 2 , R 2 = 1 , A 3 = 2 , R 3 = − 2 , A 4 = 2 , R 4 = 2 , A 5 = 3 , R 5 = 0 A_1=1,R_1=-1,A_2=2,R_2=1,A_3=2,R_3=-2,A_4=2,R_4=2,A_5=3,R_5=0 A1=1,R1=−1,A2=2,R2=1,A3=2,R3=−2,A4=2,R4=2,A5=3,R5=0。请问哪些时刻一定发生了 ϵ \epsilon ϵ的情形,哪些可能发生了?
| 1 | 2 | 3 | 4 | |
|---|---|---|---|---|
| Q 1 ( a ) Q_1(a) Q1(a) | 0 | 0 | 0 | 0 |
| Q 2 ( A 1 ) Q_2(A_1) Q2(A1) | -1 | 0 | 0 | 0 |
| Q 3 ( A 2 ) Q_3(A_2) Q3(A2) | -1 | 1 | 0 | 0 |
| Q 4 ( A 3 ) Q_4(A_3) Q4(A3) | -1 | − 2 + 1 2 = − 0.5 \frac{-2+1}{2}=-0.5 2−2+1=−0.5 | 0 | 0 |
| Q 5 ( A 4 ) Q_5(A_4) Q5(A4) | -1 | − 2 + 1 + 2 3 = 1 3 \frac{-2+1+2}{3}=\frac{1}{3} 3−2+1+2=31 | 0 | 0 |
A 1 A_1 A1可能贪心或 ϵ \epsilon ϵ-贪心选取了1号控制杆, A 2 A_2 A2可能贪心或 ϵ \epsilon ϵ-贪心选择了2号控制杆, A 3 A_3 A3贪心或 ϵ \epsilon ϵ-贪心随机选择了2号控制杆, A 4 A_4 A4如果是贪心,一定选择3或4控制杆,但是没有发生,所以一定采用了 ϵ \epsilon ϵ-贪心方法, A 5 A_5 A5如果是贪心,一定选择2控制杆( 1 3 > 0 > − 1 \frac{1}{3}>0>-1 31>0>−1),但是没有发生,所以一定发生了 ϵ \epsilon ϵ的情形。
- 在图2.2中,从累计收益和选择最佳动作的可能性的角度考虑,哪种方法会在长期表现最好?好多少?定量地表述你的答案。
ϵ = 0.01 \epsilon=0.01 ϵ=0.01会更好,因为当 t − > ∞ t->\infty t−>∞时, Q t − > q ∗ Q_t->q_* Qt−>q∗,由于 ϵ = 0.01 \epsilon=0.01 ϵ=0.01时选择最优动作的概率比 ϵ = 0.1 \epsilon=0.1 ϵ=0.1时大10倍,所以累积收益也会更大。
2.4 增量式实现
计算样本均值来估测收益所需的内存和计算量会不断增长:
Q n = R 1 + R 2 + . . . + R n − 1 n − 1 Q_n=\frac{R_1+R_2+...+R_{n-1}}{n-1} Qn=n−1R1+R2+...+Rn−1
所以设计增量式公式,以小而恒定的计算来更新平均值:
KaTeX parse error: Can't use function '$' in math mode at position 353: …] \end{aligned}$̲
这种实现只需要存储 Q n Q_n Qn和 n n n和公式(5)的少量计算。
将该公式的一般形式为:
表达式[目标 - 旧估计值]是估计值的误差,目标在上面的例子就代表第n次的收益,在向目标靠近的过程中,误差逐渐减小。
值得注意的是,上式增量式方法的步长会随时间变化。处理动作a对应的第n个收益的方法用的步长是 1 n \frac{1}{n} n1,步长可以写作 α \alpha α或者更适普地记作 α t ( a ) \alpha_t(a) αt(a)。
一个完整的使用以增量式计算的样本均值和 ϵ \epsilon ϵ-贪心动作选择的赌博机问题算法的伪代码如下所示
其中bandit(A)接受一个动作为输入,返回一个对应的收益。
2.5 跟踪一个非平稳问题
取平均收益的方法对平稳的赌博机问题是合适的,即收益的概率分布不随着时间变化的赌博机问题。
当面对非平稳的强化学习问题,给近期的收益赋予比过去很久的收益更高的权值就是一种合理的处理方式。
Q n + 1 = Q n + α [ R n − Q n ] = α R n + ( 1 − α ) Q n = α R n + ( 1 − α ) [ α R n − 1 + ( 1 − α ) Q n − 1 ] = α R n + ( 1 − α ) α R n − 1 + ( 1 − α ) 2 Q n − 1 = α R n + ( 1 − α ) α R n − 1 + ( 1 − α ) 2 α R n − 2 + . . . + ( 1 − α ) n − 1 α R 1 + ( 1 − α ) n Q 1 = ( 1 − α ) n Q 1 + ∑ i = 1 n α ( 1 − α ) n − i R i \begin{aligned} Q_{n+1} &=Q_{n}+\alpha\left[R_{n}-Q_{n}\right] \\ &=\alpha R_{n}+(1-\alpha) Q_{n} \\ &=\alpha R_{n}+(1-\alpha)\left[\alpha R_{n-1}+(1-\alpha) Q_{n-1}\right] \\ &=\alpha R_{n}+(1-\alpha) \alpha R_{n-1}+(1-\alpha)^{2} Q_{n-1} \\ &=\alpha R_{n}+(1-\alpha) \alpha R_{n-1}+(1-\alpha)^{2} \alpha R_{n-2}+\\ & \quad \quad ...+(1-\alpha)^{n-1} \alpha R_{1}+(1-\alpha)^{n} Q_{1} \\ &=(1-\alpha)^{n} Q_{1}+\sum_{i=1}^{n} \alpha(1-\alpha)^{n-i} R_{i} \end{aligned} Qn+1=Qn+α[Rn−Qn]=αRn+(1−α)Qn=αRn+(1−α)[αRn−1+(1−α)Qn−1]=αRn+(1−α)αRn−1+(1−α)2Qn−1=αRn+(1−α)αRn−1+(1−α)2αRn−2+...+(1−α)n−1αR1+(1−α)nQ1=(1−α)nQ1+i=1∑nα(1−α)n−iRi
式中, α ∈ ( 0 , 1 ] \alpha \in (0,1] α∈(0,1]是一个常数,这使得 Q n + 1 Q_{n+1} Qn+1是过去的收益和初始估计$Q_1$的加权平均,之所以是加权平均是因为我们可以验证权值的和是 ( 1 − α ) n + ∑ i = 1 n α ( 1 − α ) n − i = 1 (1-\alpha)^n+\sum_{i=1}^n \alpha(1-\alpha)^{n-i}=1 (1−α)n+∑i=1nα(1−α)n−i=1(展开之后依次提取公因式化简得到)。
注意,赋给收益 R i R_i Ri的权值 α ( 1 − α ) n − i \alpha (1-\alpha)^{n-i} α(1−α)n−i依赖于它被观测到的具体时刻 i i i与当前时刻 n n n的差,即 n − i n-i n−i。 1 − α < 1 1-\alpha<1 1−α<1,因此赋予 R i R_i Ri的权值随着相隔次数的增加而递减。事实上,由于 1 − α 1-\alpha 1−α上的指数,权值以指数形式递减(当 α = 1 \alpha=1 α=1,所有的权值都赋给最后一个收益 R n R_n Rn)。正因为如此,这个方法有时也被称为指数近因加权平均。
有时候随着时刻一步步改变步长参数是很方便的。设 α n ( a ) \alpha_n(a) αn(a)表示用于处理第 n n n次选择动作 a a a后收到的收益的步长参数。当 α n ( a ) = 1 n \alpha_n(a)=\frac{1}{n} αn(a)=n1时,就是采样平均法,大数定律保证它可以收敛到真值。然而,收敛性当然不能保证对任何步长都满足。随机逼近理论中的一个著名结果给出了保证收敛概率为1所需的条件
∑ n = 1 ∞ α n ( a ) = ∞ 且 ∑ n = 1 ∞ α n 2 ( a ) < ∞ \sum_{n=1}^\infty \alpha_n(a) = \infty 且\sum_{n=1}^\infty \alpha_n^2(a) \lt \infty n=1∑∞αn(a)=∞且n=1∑∞αn2(a)<∞
第一个条件是要求保证有足够大的步长,最终克服任何初始条件或随机波动。第二个条件保证最终步长变小,以保证收敛。
当 α n ( a ) = 1 n \alpha_n(a)=\frac{1}{n} αn(a)=n1时,(7)式满足,但是当步长为常数时,第二个条件无法满足,说明估计永远无法完全收敛,而是会随着最近得到的收益而变化。在非平稳学习中,这就是我们想要的。
练习题
- 如果步长参数 α n \alpha_n αn不是常数,写出与(6)式同样的公式。
让 α 0 = 1 \alpha_0=1 α0=1,那么 Q n + 1 = ( ∏ i = 1 n ( 1 − α i ) ) Q 1 + ∑ i = 1 n α i R i ∏ k = i + 1 n ( 1 − α k ) Q_{n+1}=\left(\prod_{i=1}^{n}\left(1-\alpha_{i}\right)\right) Q_{1}+\sum_{i=1}^{n} \alpha_{i} R_{i} \prod_{k=i+1}^{n}\left(1-\alpha_{k}\right) Qn+1=(∏i=1n(1−αi))Q1+∑i=1nαiRi∏k=i+1n(1−αk),当 x > y 且 ∏ i = x y f ( i ) = 1 x \gt y 且 \prod_{i=x}^y f(i) = 1 x>y且∏i=xyf(i)=1
- 设计并且实施一项实验来证实采用采样平均方法去解决非平稳问题的困难。使用一个10臂测试平台的修改版本,其中所有的 q ∗ ( a ) q_*(a) q∗(a)初始时相等,然后进行随机游走(比如说在每一步所有的 q ∗ ( a ) q_*(a) q∗(a)都加上一个均值为0标准差为0.01的正态分布的增量)。为其中一个使用采样平均和增量式计算的动作-价值方法,为另外一个使用常数步长参数 α = 0.1 \alpha=0.1 α=0.1的动作-价值方法,并作出如图2.2所示的图示。采用 ϵ = 0.1 \epsilon=0.1 ϵ=0.1,并且取很长的时间(比如10 000步)。
借用了GitHub上本书的官方代码求解,但是结果与书中观点相反,采样平均的方法反而有更高的平均收益和最优动作:

2.6 乐观初始值
目前为止我们讨论的所有方法都在一定程度上依赖于初始动作值 Q 1 ( a ) Q_1(a) Q1(a)的选择。从统计学角度来说,这些方法(由于初始估计值)是有偏的。对于采样平均法来说,当所有动作都至少被选择一次时,偏差就会消失。但是对于步长为 α \alpha α的情况,如公式(13)给出的偏差会随时间减小,但不会消失。如果不将它们全部设置为0,则初始值实际上变成了必须有用户选择的参数集。
如果把初始值0换成+5,由于 q ∗ ( a ) q_*(a) q∗(a)是按照均值为0,方差为1的正态分布产生的,所以+5的初始值是一个过度乐观的初始值。但是这种估计会使得动作-价值方法去试探,刚开始,无论哪一种方法被选取,收益都比最开始的估计值小,因此学习期会转向探索其他动作,所有动作在估计值收敛前都被尝试了好几次,即使每一次都按照贪心法选择动作,系统也会进行大量的试探。
图2.3展示了在一个10臂测试平台上设定初始值 Q 1 ( a ) = + 5 Q_1(a)=+5 Q1(a)=+5,并采用贪心算法的结果。为了比较同时展示了 ϵ \epsilon ϵ贪心算法使用初始值 Q 1 ( a ) = 0 Q_1(a)=0 Q1(a)=0的结果。刚开始乐观初始化方法表现得比较糟糕,因为它需要试探更多次,但是最终随着时间的推移,试探的次数减少,它的表现也变得更好,我们把这种鼓励试探的技术叫做乐观初始值。
乐观初始值是一个在平稳问题中非常有效的技巧,但它不太适合非平稳问题,因为它试探的驱动力天生是暂时的,只在开始时刻出现一次。
练习
神秘的峰值图2.3中的结果应该是相当可靠的,因为它们是2000个独立随机选择的10臂赌博机任务的平均值。那么为什么乐观估计初始化方法在曲线的早期会出现震荡和峰值呢?
就是说,刚开始在探索,在经过10次探索找到最优动作后变得贪婪(线条急剧上升),然后由于此时的奖励和最开始的估计值没有很大改变,很可能最优动作又变得不是最优动作了,所以又开始探索(线条急剧下降)。
无偏恒定步长技巧在本章中的大多数案例中,我们使用采样平均来估计动作的价值,这是因为采样平均不会像恒定步长一样产生偏差( Q n + 1 = ( 1 − α ) n Q 1 + ∑ i = 1 n α ( 1 − α ) n − i R i Q_{n+1}=(1-\alpha)^{n} Q_{1}+\sum_{i=1}^{n} \alpha(1-\alpha)^{n-i} R_{i} Qn+1=(1−α)nQ1+∑i=1nα(1−α)n−iRi有来自于 Q 1 Q_1 Q1的偏差)。然而,采样平均并不是完全令人满意的解决方案。在非平稳的问题中,它可能表现得很差。我们是否有办法既能利用恒定步长方法在非平稳过程中的优势,又能有效避免它的偏差呢?一种可行的方法是利用如下的步长来处理某个特定动作的第n个收益
β t ≐ α / o ˉ t , \beta_{t} \doteq \alpha / \bar{o}_{t}, βt≐α/oˉt,
其中, α > 0 \alpha>0 α>0是一个传统的恒定步长, o ˉ t \bar{o}_{t} oˉt是一个从零时刻开始计算的修正系数
o ˉ n ≐ o ˉ n − 1 + α ( 1 − o ˉ n − 1 ) , 对 n ≥ 0 , 满 足 o ˉ 0 ≐ 0. \bar{o}_{n} \doteq \bar{o}_{n-1} + \alpha(1-\bar{o}_{n-1}),对n \geq0,满足\bar{o}_{0} \doteq 0. oˉn≐oˉn−1+α(1−oˉn−1),对n≥0,满足oˉ0≐0.
通过与(6)式类似的分析方法,试证明 Q n Q_n Qn是一个对初始估计值无偏的指数近因加权平均。(可是这时已经不是恒定步长了吧?)
说明无偏:
因为 o ˉ 1 = α \bar{o}_{1}=\alpha oˉ1=α,所以 β 1 = 1 \beta_1=1 β1=1,由2.5第一小题的结果( Q n + 1 = ( ∏ i = 1 n ( 1 − α i ) ) Q 1 + ∑ i = 1 n α i R i ∏ k = i + 1 n ( 1 − α k ) Q_{n+1}=\left(\prod_{i=1}^{n}\left(1-\alpha_{i}\right)\right) Q_{1}+\sum_{i=1}^{n} \alpha_{i} R_{i} \prod_{k=i+1}^{n}\left(1-\alpha_{k}\right) Qn+1=(∏i=1n(1−αi))Q1+∑i=1nαiRi∏k=i+1n(1−αk)),用 β i \beta_i βi代替 α i \alpha_i αi,可知 Q n Q_n Qn不依赖于 Q 1 Q_1 Q1
说明加权平均:
余下部分表示为:
w i = β i ∏ k = i + 1 n ( 1 − β k ) w_{i}=\beta_{i} \prod_{k=i+1}^{n}\left(1-\beta_{k}\right) wi=βik=i+1∏n(1−βk)
固定n,增加i,观察到:
w i + 1 w i = β i + 1 β i ( 1 − β i + 1 ) = 1 1 − α > 1 \frac{w_{i+1}}{w_{i}}=\frac{\beta_{i+1}}{\beta_{i}\left(1-\beta_{i+1}\right)}=\frac{1}{1-\alpha}>1 wiwi+1=βi(1−βi+1)βi+1=1−α1>1
所以越久远,权值却低。我们假定了 α < 1 \alpha<1 α<1,若 α = 1 \alpha=1 α=1,则 ∀ t , β t = 1 \forall t,\beta_t=1 ∀t,βt=1
我化简(11)式最终等于 α 1 − α \frac{\alpha}{1-\alpha} 1−αα,不知道哪里出错了,暂时把过程放在这儿:
w i + 1 w i = β i + 1 β i ( 1 − β i + 1 ) = α / o ˉ i + 1 ( α / o ˉ i ) ( 1 − α / o ˉ i + 1 ) = 1 / o ˉ i + 1 ( 1 / o ˉ i ) ( 1 / α − 1 / o ˉ i + 1 ) = α o ˉ i o ˉ i + 1 − α = α o ˉ i o ˉ i + α ( 1 − o ˉ i ) − α = α 1 − α \begin{aligned} \frac{w_{i+1}}{w_{i}}&=\frac{\beta_{i+1}}{\beta_{i}\left(1-\beta_{i+1}\right)} \\ &=\frac{ \alpha / \bar{o}_{i+1}}{( \alpha / \bar{o}_{i})(1- \alpha / \bar{o}_{i+1})} \\ &=\frac{1/ \bar{o}_{i+1}}{( 1 / \bar{o}_{i})(1/\alpha- 1 / \bar{o}_{i+1})} \\ &= \frac{ \alpha\bar{o}_{i}}{\bar{o}_{i+1}-\alpha} \\ &= \frac{ \alpha\bar{o}_{i}}{\bar{o}_{i} + \alpha(1-\bar{o}_{i})-\alpha} \\ &= \frac{\alpha}{1-\alpha} \end{aligned} wiwi+1=βi(1−βi+1)βi+1=(α/oˉi)(1−α/oˉi+1)α/oˉi+1=(1/oˉi)(1/α−1/oˉi+1)1/oˉi+1=oˉi+1−ααoˉi=oˉi+α(1−oˉi)−ααoˉi=1−αα
2.7 基于置信度上界的动作选择
动作-价值估计总会存在不确定性,所以试探是必须的。虽然 ϵ − 贪 心 动 作 \epsilon-贪心动作 ϵ−贪心动作会尝试选择非贪心的动作,但是这是一种盲目的选择,因为它不大会去选择接近贪心或者不确定性特别大的动作。如果可以考虑它们的潜力来选择,也就是考虑他们的估计与最大值的距离,以及这些估计的不确定性,从长远来看,可以带来更好的收益。
A t ≐ argmax a [ Q t ( a ) + c ln t N t ( a ) ] A_{t} \doteq \underset{a}{\operatorname{argmax}}\left[Q_{t}(a)+c \sqrt{\frac{\ln t}{N_{t}(a)}}\right] At≐aargmax[Qt(a)+cNt(a)lnt]
照上面这个公式选择动作,ln t t t表示t的自然对数, N t ( a ) N_t(a) Nt(a)表示在时刻t之前动作a被选择的次数。c是一个大于0的数,它控制着试探的程度。如果 N t ( a ) = 0 N_t(a)=0 Nt(a)=0,则a就被认为是满足最大化条件的动作。
这种基于置信度上界(upper confidence bound,UCB)的动作选择的思想是,平方根项是对a动作值估计的不确定性或方差的度量。因此,最大值的大小是动作a的可能真实值的上限,参数c决定了置信水平。每次选a时,不确定性可能会减小;由于 N t ( a ) N_t(a) Nt(a)出现在不确定项的分母上,因此随着 N t ( a ) N_t(a) Nt(a)的增加,这一项就减小了。另一方面,每次选择a之外的动作时,在分子上的t增大,而 N t ( a ) N_t(a) Nt(a)却没有变化,所以不确定性增加了。自然对数的使用意味着随着时间的推移,增加会变得越来越小,但它是无限的。所有动作最终都将被选中,但是随着时间的流逝,具有较低价值估值的动作或者已经被选择了更多次的动作被选择的频率较低。
图2.4展示了在10臂测试平台上采用UCB算法的结果。如图所示,UCB往往会变现良好。但是和 ϵ \epsilon ϵ-贪心算法相比,它更难推广到本书的其他章节研究的一些更一般的强化学习问题。一个困难是在处理非平稳问题时,她主要比2.5节中介绍的方法更复杂的方法。另一个难题是要处理打的状态空间,特别是函数近似问题。
练习
UCB尖峰 在图2.4中,UCB算法的表现在第11步的时候有一个非常明显的尖峰。为什么会产生这个尖峰呢?请注意,你必须同时解释为什么收益在第11步时会增加,以及为什么在后续的若干步中会减少。(提示:如果c=1,那么这个尖峰就不会那么突出了)
这一节主要讲了一个变体的动作选择公式,以前我们只考虑了随机选择来增加试探,现在我们的试探更“有理有据”了,我们增加了一个项,它由置信水平乘以一个不确定性的度量(方差的度量)组成(我们更倾向于选择估值较大,且有较大不确定性的动作)。在前11步,智能体识别到了最大值对应的动作,会倾向于贪婪地选择这个动作,所以收益会骤增,但是随着 N t ( a ) N_t(a) Nt(a)增大,不确定性减小,而其他和该最优动作的估计值相差不大的动作的不确定性会增大,以至于大过最优动作,所以智能体再次选择“非最优动作”
官方答案:
在前10个步骤中,代理循环执行所有的动作,因为当 N t ( a ) = 0 N_t(a) = 0 Nt(a)=0时,a被认为是最大的。在第11步,代理通常会贪婪地选择。代理将继续贪婪地选择,直到ln(t)超过 N t ( a ) N_t(a) Nt(a),在这种情况下,代理将开始再次探索,从而减少奖励。
注意,在长期运行中, N t = O ( t ) N_t = O(t) Nt=O(t)并且 l n ( t ) / t → 1 ln(t)/t→1 ln(t)/t→1。所以这个智能体是渐近贪婪的。
2.8 梯度赌博机算法
目前为止,我们通过估计值来选择动作,在本节中,我们介绍通过基于偏好函数 H t ( a ) H_t(a) Ht(a)来选择动作。这里的偏好是指动作之间的相对偏好。按照如下softmax分布(吉布斯或玻尔兹曼分布)
P r { A t = a } ≐ e H t ( a ) ∑ b k e H t ( b ) ≐ π t ( a ) Pr\{A_t=a\} \doteq \frac{e^{H_t(a)}}{\sum_{b}^k e^{H_t(b)}} \doteq \pi_t(a) Pr{At=a}≐∑bkeHt(b)eHt(a)≐πt(a)
其中, π t ( a ) \pi_t(a) πt(a)是一个新的且重要的定义,用来表示动作a在时刻t被选择的概率。所有偏好函数的初始值都是一样的(例如, H 1 ( a ) = 0 , ∀ a H_1(a)=0, \forall a H1(a)=0,∀a),所以每个动作被选择的概率是相同的。
练习
证明在两种动作的情况下,softmax分布与通常在统计学和人工神经网络中使用的logistic或sigmoid函数给出的结果相同。
官方答案
令0和1分别代表两个动作,现在有
P r { A t = a } ≐ e H t ( 1 ) e H t ( 1 ) + e H t ( 0 ) = 1 1 + e − x Pr\{A_t=a\} \doteq \frac{e^{H_t(1)}}{e^{H_t(1)+e^{H_t(0)}}} =\frac{1}{1+e^{-x}} Pr{At=a}≐eHt(1)+eHt(0)eHt(1)=1+e−x1
x = H t ( 1 ) − H t ( 0 ) x=H_t(1)-H_t(0) x=Ht(1)−Ht(0),表示动作1相对于动作0的相对偏好。
基于随机梯度上升的思想,本文提出了一种自然学习算法。在每个步骤,选择动作 A t A_t At并获得收益 R t R_t Rt之后,偏好函数将会按如下方式更新
H t + 1 ( A t ) ≐ H t ( A t ) + α ( R t − R t ˉ ) ( 1 − π t ( A t ) ) , 以 及 H t + 1 ( a ) ≐ H t ( a ) + α ( R t − R t ˉ ) π t ( a ) , 对 所 有 a ≠ A t H_{t+1}(A_t) \doteq H_{t}(A_t) + \alpha (R_t-\bar{R_t})(1-\pi_t(A_t)), 以及 \\ H_{t+1}(a) \doteq H_{t}(a) + \alpha (R_t-\bar{R_t})\pi_t(a), 对所有a \not= A_t Ht+1(At)≐Ht(At)+α(Rt−Rtˉ)(1−πt(At)),以及Ht+1(a)≐Ht(a)+α(Rt−Rtˉ)πt(a),对所有a=At
其中, α \alpha α是一个大于0的数,表示步长。 R t ˉ ∈ R \bar{R_t} \in \mathbb{R} Rtˉ∈R是在时刻 t t t内所有收益的平均值,可以按2.4节所述逐步计算(若是非平稳问题,则参照2.5节)。 R t ˉ \bar{R_t} Rtˉ项作为比较收益的一个基准项。如果收益高于它,那么在未来选择动作 A t A_t At的概率就会增加,反之概率就会降低。未选择的动作被选择的概率上升。
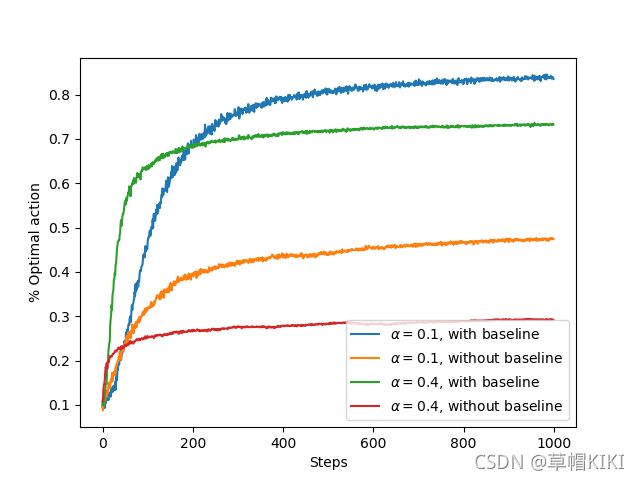
图2.5 含收益基准项与不含收益基准项的梯度赌博机算法在10臂测试平台上的平均表现,其中我们设定 q ∗ ( a ) q_*(a) q∗(a)接近于+4而不是0
图2.5展示了在一个10臂测试平台问题的变体上采用梯度赌博机算法的结果,在这个问题中,它们真实的期望收益是按照平均值为+4而不是0(方差与之前相同)的正态分布来选择的。所有收益的这种变化对剃度赌博机算法没有任何影响,因为收益基准项让它可以马上适应新的收益水平。如果没有基准项(即把公式(16)中的 R t ˉ \bar{R_t} Rtˉ设为常数0),那么性能将显著降低,如图所示:
通过随机梯度上升实现梯度赌博机算法
这部分是对(16)式的证明,比较难理解,可以跳过。
通过将梯度赌博机算法理解为梯度上升的随机近似,我们可以深入了解这一算法的本质。在精确的梯度上升算法中,每一个动作的偏好函数 H t ( a ) H_t(a) Ht(a)与增量对性能的影响成正比
H t + 1 ( a ) ≐ H t ( a ) + α ∂ E [ R t ] ∂ H t ( a ) H_{t+1}(a) \doteq H_t(a) + \alpha \frac{\partial \mathbb{E}[R_t]}{\partial H_t(a)} Ht+1(a)≐Ht(a)+α∂Ht(a)∂E[Rt]
在这里性能的衡量指标定义为总体的期望收益
E [ R t ] = ∑ x π t ( x ) q ∗ ( x ) \mathbb{E}[R_t]=\sum_x \pi_t(x) q_*(x) E[Rt]=x∑πt(x)q∗(x)
而增量产生的影响就是上述性能衡量指标对动作偏好的偏导数。当然,我们不可能真的实现精确的梯度上升,因为真实的 q ∗ ( x ) q_*(x) q∗(x)是不知道的。但是事实上,前面的更新公式(16)与公式(17)采用期望价值时是等价的,即公式(16)是随机梯度上升方法的一个实例。岁这个关系的证明只需要用初等的微积分推导几步。首先,我们仔细分析一下精确的性能梯度的定义
∂ E [ R t ] ∂ H t ( a ) = ∂ ∂ H t ( a ) [ ∑ x π t ( x ) q ∗ ( x ) ] = ∑ x q ∗ ( x ) ∂ π t ( x ) ∂ H t ( a ) = ∑ x ( q ∗ ( x ) − B t ) ∂ π t ( x ) ∂ H t ( a ) \begin{aligned} \frac{\partial \mathbb{E}\left[R_{t}\right]}{\partial H_{t}(a)} &=\frac{\partial}{\partial H_{t}(a)}\left[\sum_{x} \pi_{t}(x) q_{*}(x)\right] \\ &=\sum_{x} q_{*}(x) \frac{\partial \pi_{t}(x)}{\partial H_{t}(a)} \\ &=\sum_{x}\left(q_{*}(x)-B_{t}\right) \frac{\partial \pi_{t}(x)}{\partial H_{t}(a)} \end{aligned} ∂Ht(a)∂E[Rt]=∂Ht(a)∂[x∑πt(x)q∗(x)]=x∑q∗(x)∂Ht(a)∂πt(x)=x∑(q∗(x)−Bt)∂Ht(a)∂πt(x)
其中 B t B_t Bt被称为基准项,可以是不依赖于 x x x的标量。我们可以把它加进来,因为所有动作的梯度加起来为0, ∑ x ∂ π t ( x ) ∂ H t ( a ) = 0 \sum_x \frac{\partial \pi_t(x)}{\partial H_t(a)}=0 ∑x∂Ht(a)∂πt(x)=0。即随着 H t ( a ) H_t(a) Ht(a)的变化,一些动作的概率会增加或者减少,但是这些变化的总和为0,因为概率之和必须是1。然后我们将求和公式中的每项都乘以 π t ( x ) / π t ( x ) \pi_t(x)/\pi_t(x) πt(x)/πt(x),等式保持不变
∂ E [ R t ] ∂ H t ( a ) = ∑ x π t ( x ) ( q ∗ ( x ) − B t ) ∂ π t ( x ) ∂ H t ( a ) / π t ( x ) \frac{\partial \mathbb{E}\left[R_{t}\right]}{\partial H_{t}(a)}=\sum_{x} \pi_{t}(x)\left(q_{*}(x)-B_{t}\right) \frac{\partial \pi_{t}(x)}{\partial H_{t}(a)} / \pi_{t}(x) ∂Ht(a)∂E[Rt]=x∑πt(x)(q∗(x)−Bt)∂Ht(a)∂πt(x)/πt(x)
注意,上面的公式其实是一个“求期望”的式子:对随机变量 A t A_t At所有可能的取值 x x x进行函数求和,然后乘以对应取值的概率。可以将其简写为期望形式
= E [ ( q ∗ ( A t ) − B t ) ∂ π t ( A t ) ∂ H t ( a ) / π t ( A t ) ] = E [ ( R t − R ˉ t ) ∂ π t ( A t ) ∂ H t ( a ) / π t ( A t ) ] \begin{aligned} &=\mathbb{E}\left[\left(q_{*}\left(A_{t}\right)-B_{t}\right) \frac{\partial \pi_{t}\left(A_{t}\right)}{\partial H_{t}(a)} / \pi_{t}\left(A_{t}\right)\right] \\ &=\mathbb{E}\left[\left(R_{t}-\bar{R}_{t}\right) \frac{\partial \pi_{t}\left(A_{t}\right)}{\partial H_{t}(a)} / \pi_{t}\left(A_{t}\right)\right] \end{aligned} =E[(q∗(At)−Bt)∂Ht(a)∂πt(At)/πt(At)]=E[(Rt−Rˉt)∂Ht(a)∂πt(At)/πt(At)]
在这里我们选择 B t = R t ˉ B_t=\bar{R_t} Bt=Rtˉ,并且将 R t {R_t} Rt用 q ∗ ( A t ) q_*(A_t) q∗(At)代替。这个选择是可行的,因为 E [ R t ∣ A t ] = q ∗ ( A t ) \mathbb{E}[R_t|A_t]=q_*(A_t) E[Rt∣At]=q∗(At),而且 R t R_t Rt(给定 A t A_t At)与任何其他东西都不相关。很快我们就可以确定 ∂ π t ( x ) ∂ H t ( a ) = π t ( x ) ( 1 a = x − π t ( a ) ) \frac{\partial \pi_{t}(x)}{\partial H_{t}(a)}=\pi_{t}(x)\left(\mathbb{1}_{a=x}-\pi_{t}(a)\right) ∂Ht(a)∂πt(x)=πt(x)(1a=x−πt(a)), 1 a = x \mathbb{1}_{a=x} 1a=x表示如果a=x就取1,否则取0。假设现在我们有
= E [ ( R t − R ˉ t ) π t ( A t ) ( 1 a = A t − π t ( a ) ) / π t ( A t ) ] = E [ ( R t − R ˉ t ) ( 1 a = A t − π t ( a ) ) ] \begin{aligned} &=\mathbb{E}\left[\left(R_{t}-\bar{R}_{t}\right) \pi_{t}\left(A_{t}\right)\left(\mathbb{1}_{a=A_{t}}-\pi_{t}(a)\right) / \pi_{t}\left(A_{t}\right)\right] \\ &=\mathbb{E}\left[\left(R_{t}-\bar{R}_{t}\right)\left(\mathbb{1}_{a=A_{t}}-\pi_{t}(a)\right)\right] \end{aligned} =E[(Rt−Rˉt)πt(At)(1a=At−πt(a))/πt(At)]=E[(Rt−Rˉt)(1a=At−πt(a))]
回想一下,我们的计划是把性能指标的梯度写为某个东西的期望,这样我们就可以在每个时刻进行采样(就像我们刚刚做的那样),然后再进行与采样样本成比例地更新。将公式(17)中的性能指标的梯度用一个单独样本的期望值代替,可以得到
H t + 1 ( a ) = H t ( a ) + α ( R t − R ˉ t ) ( 1 a = A t − π t ( a ) ) , 对所有 a , H_{t+1}(a)=H_{t}(a)+\alpha\left(R_{t}-\bar{R}_{t}\right)\left(\mathbb{1}_{a=A_{t}}-\pi_{t}(a)\right), \quad \text { 对所有 } a, Ht+1(a)=Ht(a)+α(Rt−Rˉt)(1a=At−πt(a)), 对所有 a,
你会发现这和我们在公式(16)中给出的原始算法是一致的。现在我们只需要证明我们的假设 ∂ π t ( x ) ∂ H t ( a ) = π t ( x ) ( 1 a = x − π t ( a ) ) \frac{\partial \pi_{t}(x)}{\partial H_{t}(a)}=\pi_{t}(x)\left(\mathbb{1}_{a=x}-\pi_{t}(a)\right) ∂Ht(a)∂πt(x)=πt(x)(1a=x−πt(a))就可以了。回想一下两个函数的商的导数推导公式:
∂ ∂ x [ f ( x ) g ( x ) ] = ∂ f ( x ) ∂ x g ( x ) − f ( x ) ∂ g ( x ) ∂ x g ( x ) 2 \frac{\partial}{\partial x}\left[\frac{f(x)}{g(x)}\right]=\frac{\frac{\partial f(x)}{\partial x} g(x)-f(x) \frac{\partial g(x)}{\partial x}}{g(x)^{2}} ∂x∂[g(x)f(x)]=g(x)2∂x∂f(x)g(x)−f(x)∂x∂g(x)
使用这个公式我们可以得到
∂ π t ( x ) ∂ H t ( a ) = ∂ ∂ H t ( a ) π t ( x ) = ∂ ∂ H t ( a ) [ e H t ( x ) ∑ y = 1 k e H t ( y ) ] = ∂ e H t ( x ) ∂ H t ( a ) ∑ y = 1 k e H t ( y ) − e H t ( x ) ∂ ∑ y = 1 k e H t ( y ) ∂ H t ( a ) ( ∑ y = 1 k e H t ( y ) ) 2 ( 商 的 求 导 法 则 ) = 1 a = x e H t ( x ) ∑ y = 1 k e H t ( y ) − e H t ( x ) e H t ( a ) ( ∑ y = 1 k e H t ( y ) ) 2 ( 因 为 ∂ e x ∂ x = e x ) = 1 a = x e H t ( x ) ∑ y = 1 k e H t ( y ) − e H t ( x ) e H t ( a ) ( ∑ y = 1 k e H t ( y ) ) 2 = 1 a = x π t ( x ) − π t ( x ) π t ( a ) = π t ( x ) ( 1 a = x − π t ( a ) ) Q . E . D \begin{aligned} \frac{\partial \pi_{t}(x)}{\partial H_{t}(a)} &=\frac{\partial}{\partial H_{t}(a)} \pi_{t}(x) \\ &=\frac{\partial}{\partial H_{t}(a)}\left[\frac{e^{H_{t}(x)}}{\sum_{y=1}^{k} e^{H_{t}(y)}}\right] \\ &=\frac{\frac{\partial e^{H_{t}(x)}}{\partial H_{t}(a)} \sum_{y=1}^{k} e^{H_{t}(y)}-e^{H_{t}(x)} \frac{\partial \sum_{y=1}^{k} e^{H_{t}(y)}}{\partial H_{t}(a)}}{\left(\sum_{y=1}^{k} e^{H_{t}(y)}\right)^{2}} \space \space \space \space \space \space (商的求导法则)\\ &=\frac{\mathbb{1}_{a=x} e^{H_{t}(x)} \sum_{y=1}^{k} e^{H_{t}(y)}-e^{H_{t}(x)} e^{H_{t}(a)}}{\left(\sum_{y=1}^{k} e^{H_{t}(y)}\right)^{2}} \space \space \space \space \space \space (因为 \frac{\partial e^{x}}{\partial x}=e^{x} ) \\ &=\frac{\mathbb{1}_{a=x} e^{H_{t}(x)}}{\sum_{y=1}^{k} e^{H_{t}(y)}}-\frac{e^{H_{t}(x)} e^{H_{t}(a)}}{\left(\sum_{y=1}^{k} e^{H_{t}(y)}\right)^{2}} \\ &=\mathbb{1}_{a=x} \pi_{t}(x)-\pi_{t}(x) \pi_{t}(a) \\ &=\pi_{t}(x)\left(\mathbb{1}_{a=x}-\pi_{t}(a)\right) \space \space \space \space \space \space Q.E.D \end{aligned} ∂Ht(a)∂πt(x)=∂Ht(a)∂πt(x)=∂Ht(a)∂[∑y=1keHt(y)eHt(x)]=(∑y=1keHt(y))2∂Ht(a)∂eHt(x)∑y=1keHt(y)−eHt(x)∂Ht(a)∂∑y=1keHt(y) (商的求导法则)=(∑y=1keHt(y))21a=xeHt(x)∑y=1keHt(y)−eHt(x)eHt(a) (因为∂x∂ex=ex)=∑y=1keHt(y)1a=xeHt(x)−(∑y=1keHt(y))2eHt(x)eHt(a)=1a=xπt(x)−πt(x)πt(a)=πt(x)(1a=x−πt(a)) Q.E.D
我们已经证明了梯度赌博算法的期望更新与期望收益的梯度是相等的,因此该算法是随机梯度上升算法的一种。这就保证了算法具有很强的收敛性。
注意,对于收益基准项,除了要求它不依赖于所选的动作之外,不需要其他任何的假设。例如,我们可以将其设置为0或者1000,算法仍然是随机梯度上升算法的一个特例。基准项的选择不影响算法的预期更新,但它确实会影响更新值的方差,从而影响收敛速度(如图2.5所示)。采用收益的平均值作为基准项可能不是最好的,但它很简单,并且在实践中很有效。
2.9 关联搜索(上下文相关的赌博机)
本章到此为止只考虑了非关联的任务,对它们来说,没有必要将不同的动作与不同的情境联系起来。在这些任务中,当任务是平稳的时候,学习器会试图寻找一个最佳的动作;当任务是非平稳的时候,最佳动作会随着时间的变化而变化,此时它会试着去追踪最佳动作。然而,在一般的强化学习任务中,往往有不只一种情境,他们的目标是学习一种策略:一个从特定情境到最优动作的映射。为了进行一般性问题分析,下面我们简要地探讨从非关联任务推广到关联任务的最简单的方法。
举个例子,假设有一系列不同的k臂赌博机任务,每一步你都要随机地面对其中的一个。因此,赌博任务在每一步都是随机变化的。从观察者的角度来看,这是一个单一的、非平稳的k臂赌博机任务,其真正的动作价值是每步随机变化的。你可以尝试使用本章中描述的处理非平稳情况的方法,但是除非真正的动作价值的改变是非常缓慢的,否则这些方法不会有很好的效果。现在假设,当你遇到某一个k臂赌博机任务时,你会得到关于这个任务的编号的明显线索(但不是它的动作价值)。也许你面对的是一个真正的老虎机,它的外观颜色与它的动作价值集合一一对应,动作价值集合改变的时候,外观颜色也会改变。那么现在你可以学习一些任务相关的操作策略,例如,用你所看到的颜色作为信号,把每个任务和该任务下最优的动作直接关联起来,比如,如果为红色,则选择1号臂;如果为绿色,则选择2号臂。有了这种任务相关的策略,在知道任务编号信息时,你通常要比不知道任务编号信息时做得更好。
这是一个关联搜索任务的例子,因为它既设计采用试错学习去搜索最优的动作,又将这些动作与它们表现最优时的情境关联在一起。关联搜索任务现在通常在文献中被称为上下文相关的赌博机。关联搜索任务介于k臂赌博机问题和完整强化学习问题之间。它与完整强化学习问题的相似点是,它需要学习一种策略。但它又与k臂赌博机问题相似,体现在每个动作只影响即时收益。如果允许动作可以影响下一时刻的情境和收益,那么这就是完整的强化学习问题。
练习
假设你现在正面对着一个2臂赌博机任务,而它的真实动作价值是随时间变化的。特别地,假设对任意的时间,动作1和2的真实价值有50%的概率是0.1和0.2(情况A),50%的概率是0.9和0.8(情况B)。如果在每一步时你无法确认面对的是哪种情况,那么这时最优的期望成功值是多少?你如何才能得到它?现在假设每一步你被告知了情况是A还是B(但你仍不知道真实价值,只能够区分是不同情况)。这就是一个关联搜索的任务。对这个任务,最优的期望成功值又是多少?你应该采取什么样的策略才能达到最优?
①无法确认情况
动作1: 0.5 × 0.1 + 0.5 × 0.9 = 0.5 0.5 \times 0.1+0.5 \times 0.9=0.5 0.5×0.1+0.5×0.9=0.5
动作2: 0.5 × 0.2 + 0.5 × 0.8 = 0.5 0.5 \times 0.2 + 0.5 \times 0.8 = 0.5 0.5×0.2+0.5×0.8=0.5
最优期望值为0.5,选择任意动作都可以
②可以确认情况,但仍未知真实价值
真实情况下,在情况1应该选择动作2,在情况2应该选择动作1
所以最优期望值为: 0.5 × 0.9 + 0.5 × 0.2 = 0.55 0.5 \times 0.9 + 0.5 \times 0.2=0.55 0.5×0.9+0.5×0.2=0.55
2.10 本章小结
本章介绍了几种平衡试探和开发的简单方法:
-
ϵ \epsilon ϵ-贪心方法
- 小概率随机选择动作,大概率贪心选择收益估计值最大的动作
-
UCB方法
- 置信度上界方法,采用确定的动作选择,选择那些具有较少样本的动作进行试探
-
剃度赌博机算法
- 不估计动作价值,而是利用偏好函数,使用softmax分布来以一种分级的、概率式的方法选择更优的动作。
-
乐观初始值设置
- 在开始时刻让贪心方法也能进行显式试探
哪种方法最好?
一个难题是它们都有一个参数,为了进行一个有意义的比较,我们将把它们的性能看作关于它们参数的一个函数。
之前我们已经给出了每种算法及参数随时间推移的学习曲线。在这里我们总结了一个完整的精简的学习曲线,展示了每种算法和参数超过1000步的平均收益值,这个值与学习曲线下的面积成正比。
图2.6显示了这章中各种赌博机算法的性能曲线,每条算法性能曲线都被看做一个自己参数的函数,x轴用单一的尺度显示了所有的参数。这种类型的图称为参数研究图。需要注意的是,x轴上参数值的变化是2的倍数,并以对数坐标表现。由图可见,每个算法性能曲线呈倒U形;所有算法在其擦拿书的中间值处表现最好。
在评估一种方法的时候,我们不仅要关注它在最佳参数设置上的表现,还要注意它对参数值的敏感性。所有这些算法都是相当不敏感的,它们在一系列参数值上表现得很好(这些参数值的大小是一个数量级的)。在用本章的10臂测试平台上运行比较时,UCB似乎表现最好
其他平衡试探和开发的方法:
- Gittins指数
- 更具一般性
- 需要已知可能问题的先验分布
- 贝叶斯方法
- 假定已知动作价值的初始分布,然后在每步之后更新分布(假定真实的动作价值是平稳的)
- 计算可能非常复杂,但对于某些特殊分布(共轭先验)则很容易
练习
为在练习2.5中提出的非平稳情况作一张类似2.6的图。包括 α = 0.1 \alpha=0.1 α=0.1的恒定步长 ϵ \epsilon ϵ-贪心算法。运行200 000步,并将过去100 000步的平均收益作为每个算法和参数集的性能度量。
(没做,运行太费时间)