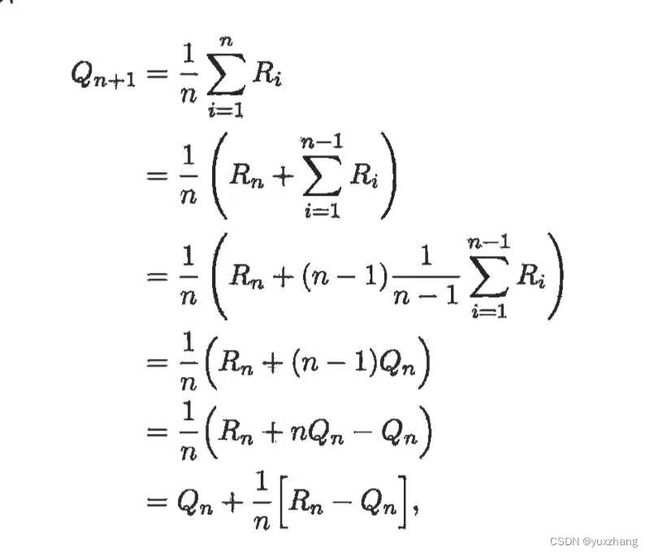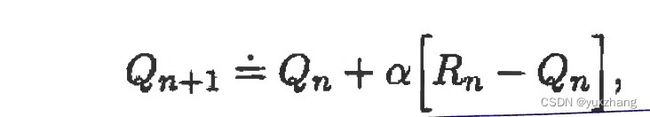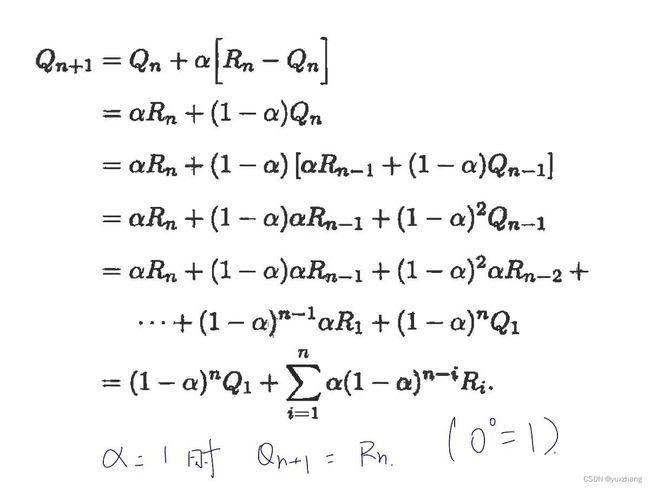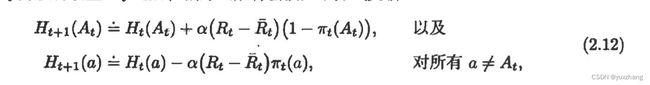强化学习导论（第二版）第二章 多臂赌博机

目录

前言

一、什么是多臂赌博机？

二、主要内容

1.K臂赌博机问题

2.增量式实现

 3.跟踪一个非平稳问题

 4.乐观初始值

5.基于置信度上界的动作选择

6.梯度赌博机算法 

 7.上下文相关的赌博机

总结

---

---

前言

本人小白，第一次写博客，有问题和不对的地方欢迎评论区指正。

本书的第一章大部分为概念性内容，本篇博客的目的是想将强化学习的内容结合实际用习题和代码来展现出来。因此，直接而从第二章开始。

但是有一个地方需要强调，强化学习与监督学习和无监督学习的辨识：

监督学习：有标签、有特征，学习标签与特征之间的关系。典型例子：分类。

无监督学习：有特征、无标签。典型例子：聚类。

强化学习：同样使用无标签的数据，但是有反馈信号，也就是我们说的奖励与惩罚，通过这种模式向目标靠近。

---

一、什么是多臂赌博机？

k臂赌博机这个词来源于“老虎机”，就是有k个手柄，每一次选择一个手柄，得到一个奖励，当然每次选择时同一个手柄对应的奖励是不固定的，我们的目的是最大化这个奖励。

二、主要内容

1.K臂赌博机问题

k:k个动作，每个动作在被选择时都有一个对应收益，我们称之为“价值”。

符号表示：

:t时刻选择的动作，对应的收益记作 。

任一动作a对应的价值，记作,是给定动作a时收益的期望。

当然了，如果知道每个拉杆对应的收益，那么我们选择最大收益就可以了，但是实际上我们是不知道的，所以我们需要对动作a在时刻t的价值进行估计，这个估计记作 ,我们希望它接近。

 在估计了拉杆的价值后，接下来就需要选择拉杆，那么拉杆的选择方式是什么呢，下面我们来讨论这个问题。

我们的目的是最大化收益，其实最简单的想法就是贪心算法，每次都选择最大的收益对应的动作，但是，我们可以想象这种方法可能会出现有些拉杆始终未被选择，在这里我把它理解为局部最优。

所以为了跳出局部最优我们需要加入一些随机性。

在这本书中，贪心的动作称为“开发”，随机选择的动作称为“试探”。

开发可以短期内获得最好收益，但是试探虽然短期内收益可能不太好，但长远来看收益更高。

开发和试探是冲突的，我们追求的是二者的平衡。

1.采样平均法（估计动作价值的方法）

=t时刻前通过执行a动作获得的收益总和 / t时刻前执行动作a的次数

当次数为0时，可以给定一个值比如0。这就类似于没执行的动作初始化价值为0

2.动作-价值方法（选择方法）

使用动作的价值的估计来进行动作的选择。

上面我们提到的贪心动作选择可以记作：

上面也说了这个办法有缺陷，为了弥补缺陷，书中提出了方法，这个方法就是以一个很小的概率随机选择动作，的概率贪心选择动作。这个算法的一个优点是，如果时刻无限长，那么每一个动作都会被无限次采样，从而确保所有的 收敛到 。这就意味着选择最优动作的概率会收敛到大于，接近确定性选择。

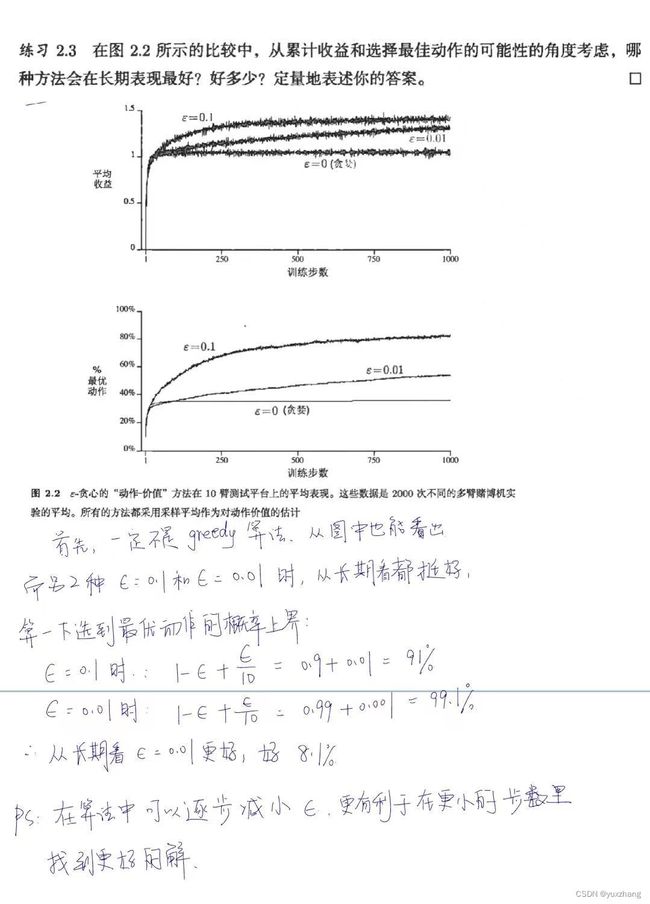
题2.1：

 题2.2：

题2.3：

2.增量式实现

在估计时，为了高效计算均值，我们将其归结到单个动作。

令表示这一动作被选择i次后获得的收益，表示被选择n-1次后它的估计的动作价值，简写为：

更新公式：

新估计值旧估计值+步长✖[目标-旧估计值]

步长用或表示。

 3.跟踪一个非平稳问题

前面的取平均方法对平稳赌博机问题是合适的，但如果赌博机的收益的概率分布会随着时间变化的话，那此方法就不合适了。现实生活中我们经常遇到的也是非平稳问题。

对此进行如下改进：

此方法称为加权平均或者指数近因加权平均 。 

为保证步长收敛概率为1，有随机逼近定理：

 题2.4：

题2.5：

代码如下：

import matplotlib
import matplotlib.pyplot as plt
import numpy as np
from tqdm import trange

matplotlib.use('Agg')


class Bandit:
    # @k_arm: # of arms
    # @epsilon: probability for exploration in epsilon-greedy algorithm
    # @initial: initial estimation for each action
    # @step_size: constant step size for updating estimations
    # @sample_averages: if True, use sample averages to update estimations instead of constant step size
    # @UCB_param: if not None, use UCB algorithm to select action
    # @gradient: if True, use gradient based bandit algorithm
    # @gradient_baseline: if True, use average reward as baseline for gradient based bandit algorithm
    def __init__(self, k_arm=10, epsilon=0., initial=0., step_size=0.1, sample_averages=False, true_reward=0.):
        self.k = k_arm
        self.step_size = step_size
        self.sample_averages = sample_averages
        self.indices = np.arange(self.k)
        self.time = 0
        self.average_reward = 0
        self.true_reward = true_reward
        self.epsilon = epsilon
        self.initial = initial

    def reset(self):
        # real reward for each action
        self.q_true = np.random.randn(self.k) + self.true_reward

        # estimation for each action
        self.q_estimation = np.zeros(self.k) + self.initial

        # # of chosen times for each action
        self.action_count = np.zeros(self.k)

        self.best_action = np.argmax(self.q_true)

        self.time = 0

    # get an action for this bandit
    def act(self):
        if np.random.rand() < self.epsilon:
            return np.random.choice(self.indices)

        q_best = np.max(self.q_estimation)
        return np.random.choice(np.where(self.q_estimation == q_best)[0])

    # take an action, update estimation for this action
    def step(self, action):
        # generate the reward under N(real reward, 1)
        reward = np.random.normal(loc=0.0,scale=0.01,size=None) + self.q_true[action]
        self.time += 1
        self.action_count[action] += 1
        self.average_reward += (reward - self.average_reward) / self.time

        if self.sample_averages==1:
            # update estimation using sample averages
            self.q_estimation[action] += (reward - self.q_estimation[action]) / self.action_count[action]
        elif self.sample_averages==2:
            self.q_estimation[action] += (reward - self.q_estimation[action]) / 0.1
        return reward


def simulate(runs, time, bandits):
    rewards = np.zeros((len(bandits), runs, time))
    best_action_counts = np.zeros(rewards.shape)
    for i, bandit in enumerate(bandits):
        for r in trange(runs):
            bandit.reset()
            for t in range(time):
                action = bandit.act()
                reward = bandit.step(action)
                rewards[i, r, t] = reward
                if action == bandit.best_action:
                    best_action_counts[i, r, t] = 1
    mean_best_action_counts = best_action_counts.mean(axis=1)
    mean_rewards = rewards.mean(axis=1)
    return mean_best_action_counts, mean_rewards
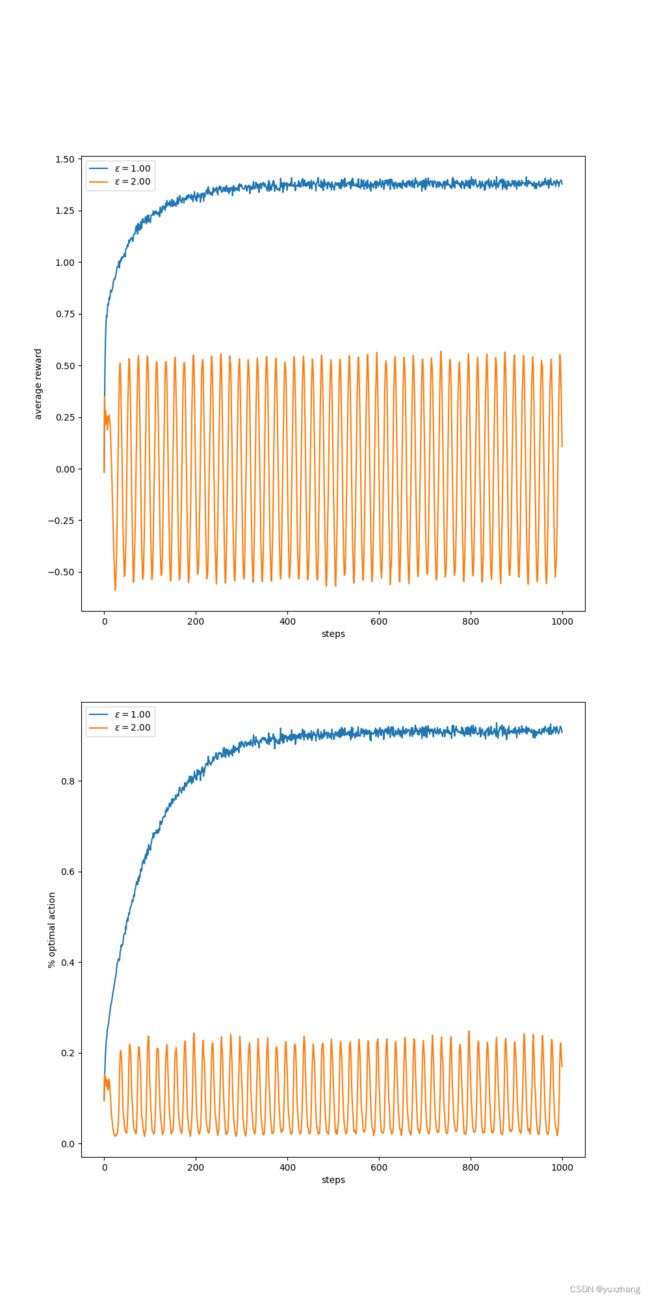
def figure_2_2(runs=2000, time=1000):
    epsilons = [1,2]
    bandits = [Bandit(epsilon=0.1, sample_averages=eps) for eps in epsilons]
    best_action_counts, rewards = simulate(runs, time, bandits)

    plt.figure(figsize=(10, 20))

    plt.subplot(2, 1, 1)
    for eps, rewards in zip(epsilons, rewards):
        plt.plot(rewards, label='$\epsilon = %.02f$' % (eps))
    plt.xlabel('steps')
    plt.ylabel('average reward')
    plt.legend()

    plt.subplot(2, 1, 2)
    for eps, counts in zip(epsilons, best_action_counts):
        plt.plot(counts, label='$\epsilon = %.02f$' % (eps))
    plt.xlabel('steps')
    plt.ylabel('% optimal action')
    plt.legend()

    plt.savefig('figure_2_22.png')
    plt.close()
figure_2_2()

运行结果：

 4.乐观初始值

这部分相对简单，其实就是初始化时给定一足够大的值，不全初始化为0，这样可以一定程度上保证每个情况都可以被选择到。在这里不做过多解释，给出例题。

题2.6：

题2.7：

5.基于置信度上界的动作选择

上面提到了的选择方法，但是实际上这个方法是一种盲目的试探，他不会去倾向于选择接近贪心或不确定性特别大的动作，在非贪心动作中，最好是根据它们的潜力来选择可能事实上是最优的动作，这就要考虑到它们的估计有多大的可能接近最大值，以及这些估计的不确定性。

于是给出以下公式：

式中平方根是对动作a值估计的不确定性或方差的度量，每次选择a时不确定性会减小。c决定了置信水平。

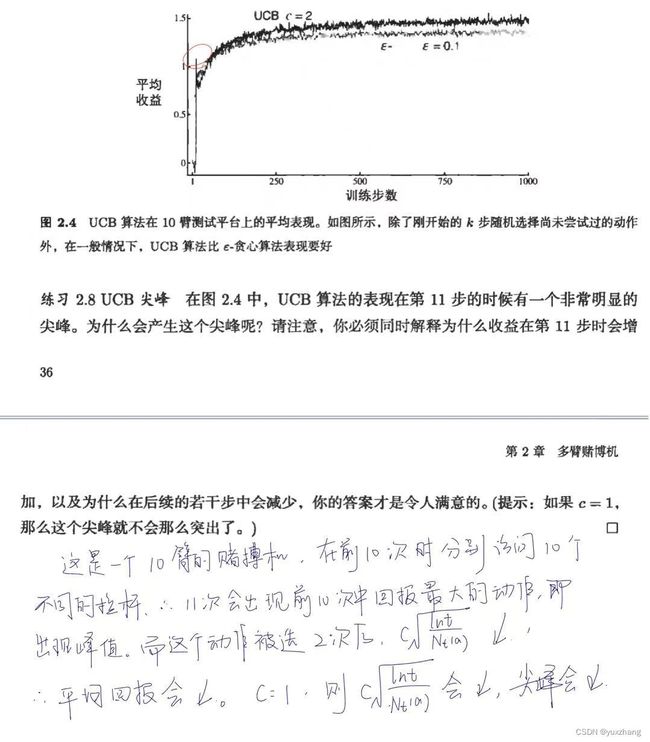
题2.8：

6.梯度赌博机算法 

设置偏好函数，偏好函数越大，动作就会越频繁的被选择，但偏好函数的概念不是从“收益“的意义上提出的。（只有一个动作对另一个动作的相对偏好才是重要的）

softmax分布：

偏好函数的更新：

 

题2.9：

 

梯度下降相关代码：

def act(self):
    exp_est = np.exp(self.q_estimation)
    self.action_prob = exp_est / np.sum(exp_est)
    return np.random.choice(self.indices, p=self.action_prob)

       
 # take an action, update estimation for this action
def step(self, action):
    # generate the reward under N(real reward, 1)
    reward = np.random.randn() + self.q_true[action]
    self.time += 1
    self.action_count[action] += 1
    self.average_reward += (reward - self.average_reward) / self.time
    one_hot = np.zeros(self.k)
    one_hot[action] = 1
    return reward

 7.上下文相关的赌博机

在这里只给出例题及答案：

题2.10：

---

 

总结

以上就是本章的全部内容。