二叉树、二叉查找树
二叉树、二叉查找树
目录:
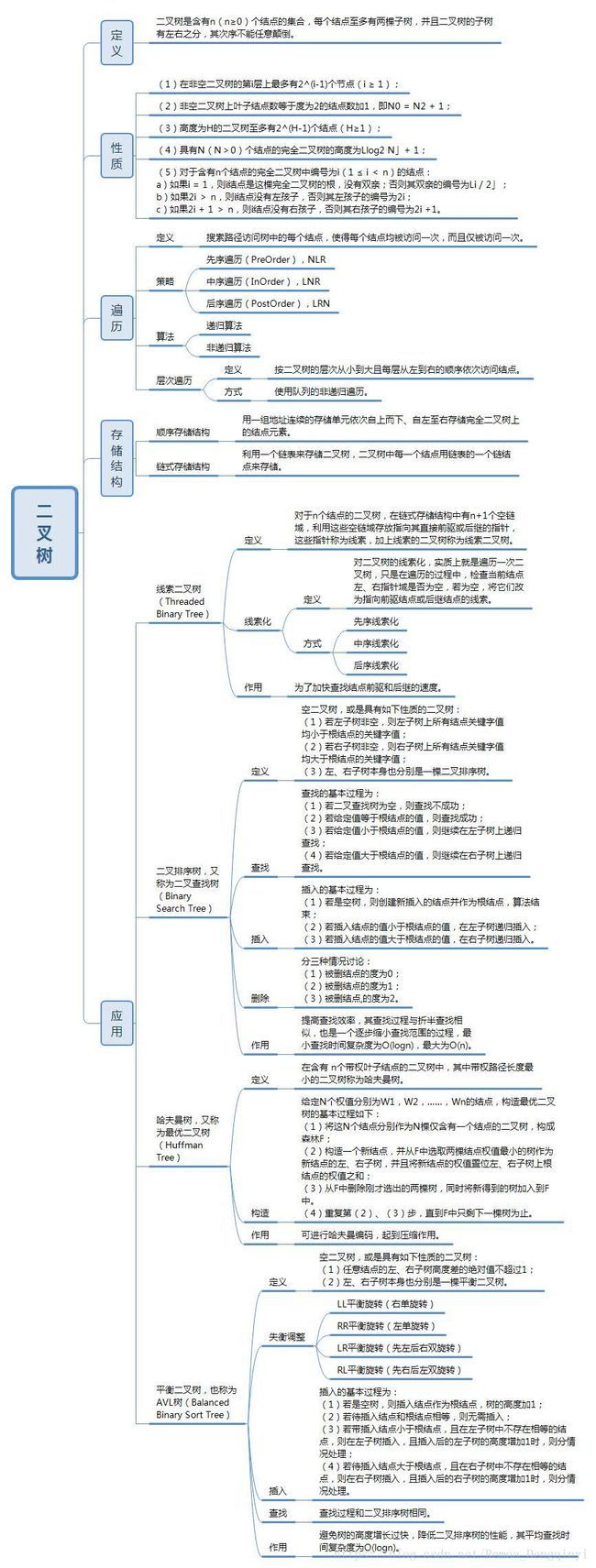
1、二叉树思维导图:
A)定义;B)性质;C)遍历;D)存储结构;E)应用
2、二叉查找树抽象数据类型实现:
A)查找;B)删除;C)插入;D)销毁;E)计算深度;F)遍历;G)求前驱结点;H)求后继结点
1、二叉树思维导图:
2、二叉查找树抽象数据类型实现:
(1)源码:
/**
* 二叉查找树(BST)抽象数据类型实现
**/
#include
#include
#include
#include
#define RAND_NUM_START 1 //生成随机数的值的3开始范围
#define RAND_NUM_END 100 //生成随机数的值的结束范围
#define RAND_NUM_COUNT 10 //生成随机数的数目
#define MAX_SIZE 100 //测试用例的最大数目
#define EXCEPTION -1 //内存异常
#define TRUE 1 //函数结果状态码
#define FALSE 0 //函数结果状态码
typedef int KeyType; //这里定义值类型为整型
typedef int Status; //这里定义函数结果返回类型为整型
typedef struct ElemType{ //数据元素类型定义
int key; //值
}ElemType;
typedef struct BSTNode{ //二叉查找树存储结构类型定义
ElemType data; //数据元素
struct BSTNode *lchild, *rchild; //左右孩子指针
}BSTNode, *BSTree;
//构造一棵二叉查找树
Status InitBST(BSTree &t, ElemType elem[]);
//查找值为key的结点
Status SearchBST(BSTree t, KeyType key);
//插入值为elem.key的结点
Status InsertBST(BSTree &t, ElemType elem);
//删除树中其值为key的结点
Status DeleteBST(BSTree &t, KeyType key);
//销毁树
Status DestoryBST(BSTree t);
//得到一个结点的双亲结点
BSTree GetParent(BSTree t, KeyType key, BSTree &parent, BSTree &firstRightParent, BSTree &firstLeftParent);
//得到值为key的结点的前驱结点
BSTree GetPredecessor(BSTree t, KeyType key);
//得到值为key的结点的后继结点
BSTree GetSuccessor(BSTree t, KeyType key);
//中序遍历
Status InOrderTraversal(BSTree t);
//输出当前指针所指的结点的值
Status Visit(ElemType e);
//求二叉查找树深度
Status GetTreeDepth(BSTree t);
//查找树中结点的最大值
BSTree GetMaximum(BSTree t);
//查找树中结点的最小值
BSTree GetMinimum(BSTree t);
//获得随机数列
Status GetRandom(ElemType *array);
//输出二叉查找树
Status PrintTree(BSTree t);
//菜单函数
void Menu();
//构造一棵二叉查找树
Status InitBST(BSTree &t, ElemType elem[]){
t = NULL;
for(int i = 0; i < RAND_NUM_COUNT; i++){
InsertBST(t, elem[i]);
}
return TRUE;
}
//查找值为key的结点
Status SearchBST(BSTree t, KeyType key){
if(t == NULL){
return NULL;
}
if(key == t->data.key){
return TRUE;
}
if(key > t->data.key){
t = t->rchild;
return SearchBST(t, key);
}else{
t = t->lchild;
return SearchBST(t, key);
}
}
//插入值为elem.key的结点
Status InsertBST(BSTree &t, ElemType elem){
if(t == NULL){
BSTNode *s;
s = (BSTree)malloc(sizeof(BSTNode));
if(s == NULL){
return EXCEPTION;
}
s->data = elem;
s->lchild = NULL;
s->rchild = NULL;
t = s;
return TRUE;
}
if(elem.key > t->data.key){
return InsertBST(t->rchild, elem);
}
if(elem.key < t->data.key){
return InsertBST(t->lchild, elem);
}
return FALSE;
}
//删除树中其值为key的结点
Status DeleteBST(BSTree &t, KeyType key){
BSTree p, s, tmp;
if(t == NULL){
return FALSE;
}
if(key == t->data.key){
tmp = t;
if(tmp->lchild == NULL){
t = tmp->rchild;
free(tmp);
}else if(tmp->rchild == NULL){
t = tmp->lchild;
free(tmp);
}else{
p = tmp;
s = tmp->lchild;
while(NULL != s->rchild){
p = s;
s = s->rchild;
}
tmp->data = s->data;
if(p != tmp){
p->rchild = s->lchild;
}else{
p->lchild = s->lchild;
}
free(s);
}
return TRUE;
}
if(key > t->data.key){
return DeleteBST(t->rchild, key);
}else{
return DeleteBST(t->lchild, key);
}
}
//销毁树
Status DestoryBST(BSTree t){
if(t != NULL){
DestoryBST(t->lchild);
DestoryBST(t->rchild);
free(t);
}
return TRUE;
}
/**
* 得到一个结点的双亲结点
* parent:双亲结点
* firstRightParent:最后一次在查找路径中出现右拐的结点
* firstLeftParent:最后一次在查找路径中出现左拐的结点
**/
BSTree GetParent(BSTree t, KeyType key, BSTree &parent, BSTree &firstRightParent, BSTree &firstLeftParent){
while(t != NULL){
if(t->data.key == key){
return t;
}
parent = t;
if(t->data.key > key){
firstLeftParent = t;
t = t->lchild;
}else{
firstRightParent = t;
t = t->rchild;
}
}
return NULL;
}
//得到值为key的结点的前驱结点
BSTree GetPredecessor(BSTree t, KeyType key){
if(t == NULL){
return NULL;
}
BSTree parent = NULL, firstRightParent = NULL, firstLeftParent = NULL;
BSTree node = GetParent(t, key, parent, firstRightParent, firstLeftParent);
if(node == NULL){
return NULL;
}
if(node->lchild != NULL){
return GetMaximum(node->lchild);
}
if(firstRightParent == NULL){
return NULL;
}
if(node == parent->rchild){
return parent;
}
if(node == parent->lchild){
return firstRightParent;
}
return NULL;
}
//得到值为key的结点的后继结点
BSTree GetSuccessor(BSTree t, KeyType key){
if(t == NULL){
return FALSE;
}
BSTree parent = NULL, firstRightParent = NULL, firstLeftParent = NULL;
BSTree node = GetParent(t, key, parent, firstRightParent, firstLeftParent);
if(node == NULL){
return NULL;
}
if(node->rchild != NULL){
return GetMinimum(node->rchild);
}
if(firstLeftParent == NULL){
return NULL;
}
if(node == parent->lchild){
return parent;
}
if(node == parent->rchild){
return firstLeftParent;
}
return NULL;
}
//中序遍历
Status InOrderTraversal(BSTree t){
if(t != NULL){
InOrderTraversal(t->lchild);
Visit(t->data);
InOrderTraversal(t->rchild);
}
return TRUE;
}
//输出当前指针所指的结点的值
Status Visit(ElemType e){
printf("%d ", e.key);
return TRUE;
}
//求二叉查找树深度
Status GetTreeDepth(BSTree t){
if(NULL == t){
return 0;
}
int depthLeft = 0, depthRight = 0;
depthLeft = GetTreeDepth(t->lchild);
depthRight = GetTreeDepth(t->rchild);
return 1 + (depthLeft > depthRight ? depthLeft : depthRight);
}
//查找树中结点的最大值
BSTree GetMaximum(BSTree t){
if(t == NULL){
return NULL;
}
while(t->rchild != NULL){
t = t->rchild;
}
return t;
}
//查找树中结点的最小值
BSTree GetMinimum(BSTree t){
if(t == NULL){
return FALSE;
}
while(t->lchild != NULL){
t = t->lchild;
}
return t;
}
//获得随机数列
Status GetRandom(ElemType *array){
Status tmp;
int j;
srand((int)time(0));
for(int i = 0; i < RAND_NUM_COUNT; ){
tmp = rand()%(RAND_NUM_END - RAND_NUM_START + 1) + RAND_NUM_START;
for(j = 0; j < i; j++){
if(array[j].key == tmp){
break;
}
}
if(j == i){
array[i].key = tmp;
i++;
}
}
return TRUE;
}
//输出二叉查找树
Status PrintTree(BSTree t){
if(t == NULL){
return FALSE;
}
printf("%d ", t->data.key);
if(t->lchild || t->rchild ){
printf("(");
PrintTree(t->lchild);
if(t->rchild){
if(t->lchild == NULL){
printf("#");
}
printf(", ");
}else{
printf(", #");
}
PrintTree(t->rchild);
printf(")");
}
return TRUE;
}
//菜单函数
void Menu(){
printf("-------------二叉查找树操作选项--------------\n");
printf("| 1 返回菜单 |\n");
printf("| 2 退出程序 |\n");
printf("| 3 随机创建一棵二叉查找树 |\n");
printf("| 4 二叉查找树的查找 |\n");
printf("| 5 二叉查找树的插入 |\n");
printf("| 6 二叉查找树的删除 |\n");
printf("| 7 二叉查找树的销毁 |\n");
printf("| 8 二叉查找树的深度计算 |\n");
printf("| 9 二叉查找树的中序遍历 |\n");
printf("| 10 打印二叉查找树 |\n");
printf("| 11 二叉查找树某结点的前驱结点 |\n");
printf("| 12 二叉查找树某结点的后继结点 |\n");
printf("| 13 二叉查找树结点最大值 |\n");
printf("| 14 二叉查找树结点最小值 |\n");
printf("-------------------------------------------\n");
}
int main(){
int choose, i;
KeyType key;
BSTree t = NULL, result = NULL;
Menu();
while(TRUE){
printf("按输入序号(1-14)以选择要执行的操作: ");
scanf_s("%d",&choose);
switch(choose){
case 1:
Menu();
break;
case 2:
exit(0);
case 3:
ElemType array[MAX_SIZE];
memset(array, 0, MAX_SIZE);
GetRandom(array);
printf("选取的随机数为:");
for(i = 0; i < RAND_NUM_COUNT; i++){
printf("%d ",array[i].key);
}
if(InitBST(t,array)){
printf("\n创建二叉查找树成功!\n");
printf("输出该树中的结点之间的关系:");
if(PrintTree(t)){
printf("\n");
}else{
printf("打印失败。\n");
}
}else{
printf("\n创建二叉查找树失败!\n");
}
break;
case 4:
printf("请输入一个要查找的数据:");
scanf_s("%d",&key);
if(SearchBST(t, key)){
printf("查找完毕,在树中找到该数据。\n");
}else{
printf("查找完毕,不存在该数据。\n");
}
break;
case 5:
printf("请输入一个要插入的数据:");
scanf_s("%d",&key);
ElemType elem;
elem.key = key;
if(InsertBST(t, elem)){
printf("插入成功!插入后的新树为:\n");
if(PrintTree(t)){
printf("\n");
}else{
printf("树为空,打印失败。\n");
}
}else{
printf("该值已存在,插入失败。\n");
}
break;
case 6:
printf("请输入一个要删除的数据:");
scanf_s("%d",&key);
if(DeleteBST(t, key)){
printf("删除成功。删除后的新树为:\n");
if(PrintTree(t)){
printf("\n");
}else{
printf("树为空,打印失败。\n");
}
}else{
printf("删除失败,树为空或树中不存在该数据。\n");
}
break;
case 7:
if(DestoryBST(t)){
printf("销毁成功!\n");
t = NULL;
break;
}else{
printf("销毁失败!\n");
break;
}
case 8:
printf("树的深度为:%d\n",GetTreeDepth(t));
break;
case 9:
printf("中序遍历的结果为:");
if(t != NULL){
InOrderTraversal(t);
printf("\n");
}else{
printf("树为空,遍历失败。");
}
break;
case 10:
if(PrintTree(t)){
printf("\n");
}else{
printf("树为空,打印失败。\n");
}
break;
case 11:
printf("请输入待查找结点的前驱结点的值:");
scanf_s("%d",&key);
result = GetPredecessor(t, key);
if(result != NULL){
printf("结点%d的前驱结点的值为:%d\n", key, result->data.key);
}else{
printf("树为空或待查找结点的前驱结点不存在或该结点不存在,查找失败。\n");
}
break;
case 12:
printf("请输入待查找结点的后继结点的值:");
scanf_s("%d",&key);
result = GetSuccessor(t, key);
if(result != NULL){
printf("结点%d后继结点的值为:%d\n", key, result->data.key);
}else{
printf("树为空或待查找结点的后继结点不存在或该结点不存在,查找失败。\n");
}
break;
case 13:
result = GetMaximum(t);
if(result != NULL){
printf("树中结点的最大值为:%d\n", result->data.key);
}else{
printf("树为空,查找失败。\n");
}
break;
case 14:
result = GetMinimum(t);
if(result != NULL){
printf("树中结点的最小值为:%d\n", result->data.key);
}else{
printf("树为空,查找失败。\n");
}
break;
default:
printf("输入的数字有误,请重新输入!\n");
break;
}
}
system("pause");
} (2)运行结果:
a)菜单栏功能展示:
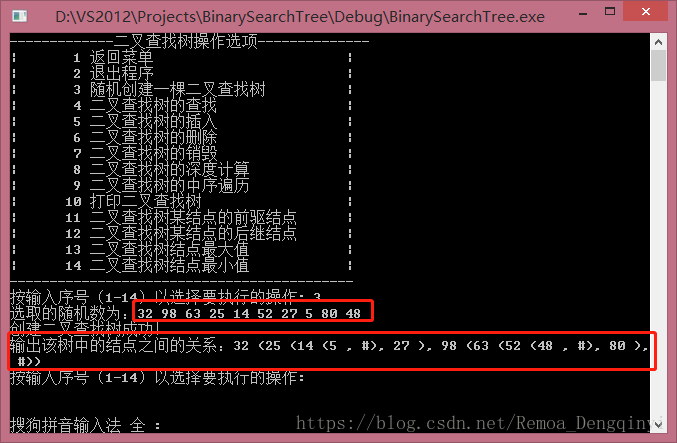
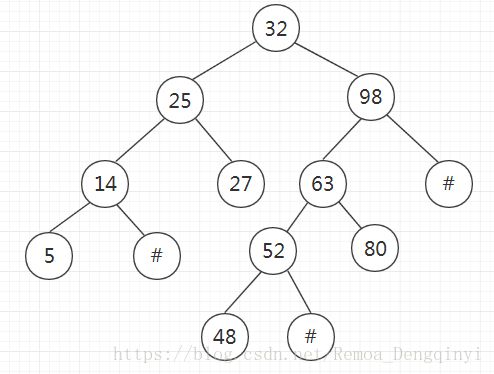
b)通过随机数随机生成一个结点数目为10的初始化二叉查找树:
示意图如下:
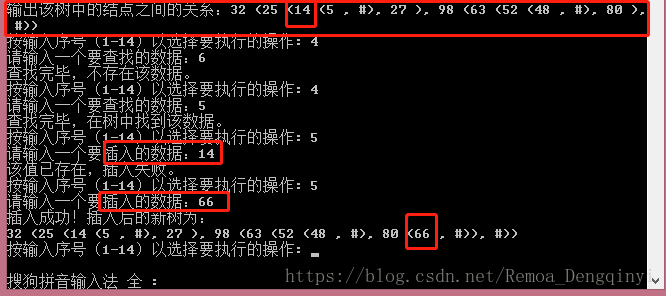
c)查找值为key的结点:
d)插入值为elem.key的结点:
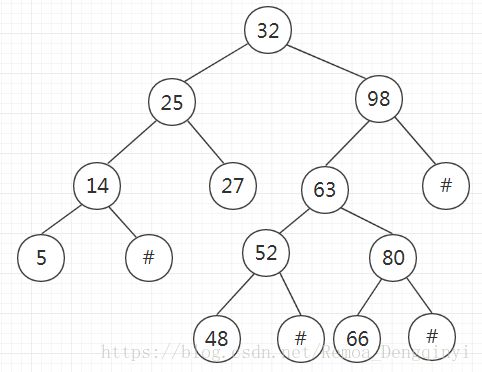
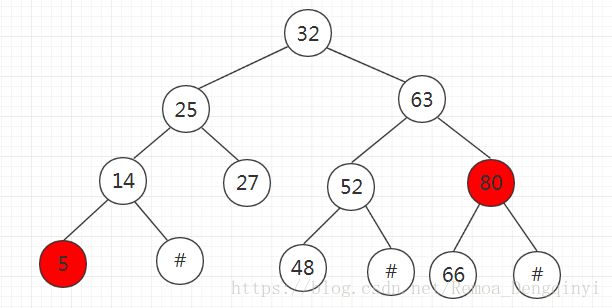
插入值为66的结点后,示意图如下:
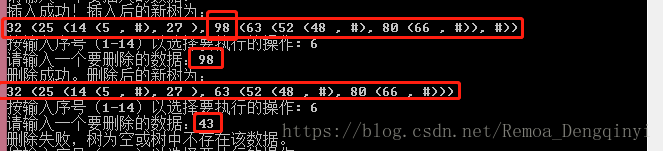
e)删除树中其值为key的结点:
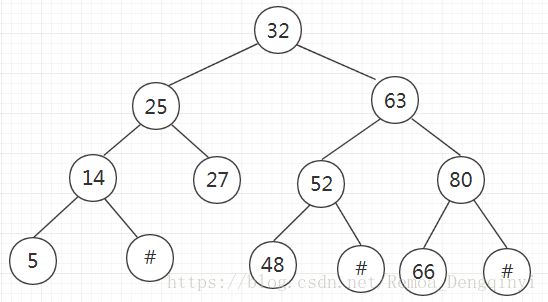
删除值为98的结点后,示意图如下:
f)求树的深度:
g)中序遍历该树:
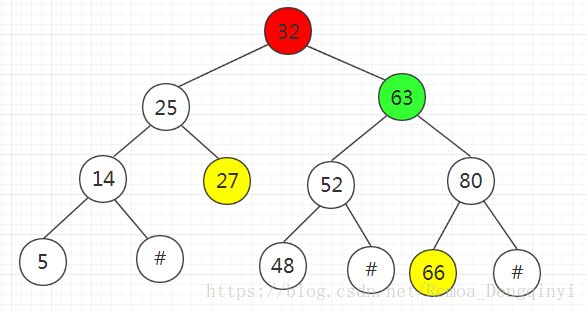
h)求某结点的前驱结点及后继结点:
示意图如图所示(27的后继结点用红色表示,66的前驱结点用绿色表示):
i)查找树中结点的最大值和最小值:
示意图如图所示: