基本题型记录-二叉树中序遍历

由于本人基础较差，所以针对部分题型做一个记录，以免自己忘记

1、二叉树中序遍历

这个遍历方法可以搜一下博客上很多讲解，这里主要是记录一下代码实现，以下面的二叉树为例子

结果应该是

2、迭代法

2.1 遍历过程

这里借用了一个临时的栈（先访问的后处理），存储对应的根节点以及左子树对应的节点，整个过程基本上是不断访问子树（先左，后根，然后右），将根节点推入栈，当访问到最后一个根节点的左子树节点为空时，从栈顶取出对应元素，再访问其右子树节点，判断其是否有左右子树再进行操作。

1. 从根节点（23）开始，curr开始指向原始根节点
   

2. 指向根节点元素（23）压入栈中（根节点往往后面才会处理，所以我们先将其放入栈底）
   

3. 找到当前节点的左子树节点（34），curr=curr.left
   

4. 当前移动后的curr（指向34）不为空的话，则将其推入栈中
   

5. 继续找当前节点（34）的左子节点（方法同上一个节点，若不为空则推入栈中）
   
   

6. 直到左子树节点为空（即图示所示77对应的节点左子节点为空），取对应栈顶元素
   此时说明该节点无左子树，根据中序遍历左跟右的顺序，左子树为空，此时应该读取根节点元素（即取出对应的栈顶元素），这里77即为我们中序遍历的第一个节点
   

7. 访问77对应右子树节点
   为空则说明这个节点对应无右子树，那么也就不用访问其对应右节点
   
   至此，以77为根节点的左子树访问完毕

8. 访问以77作为左子节点的根节点99（从栈中取出对应根节点，栈顶元素99）
   访问完栈顶元素以后，一定紧接着访问右子树
   

9. 访问以99为根节点的右子树，若其不为空，则压入栈中作为右子树的根节点
   

10. 查询以90为根节点的右子树是否有左子节点
    
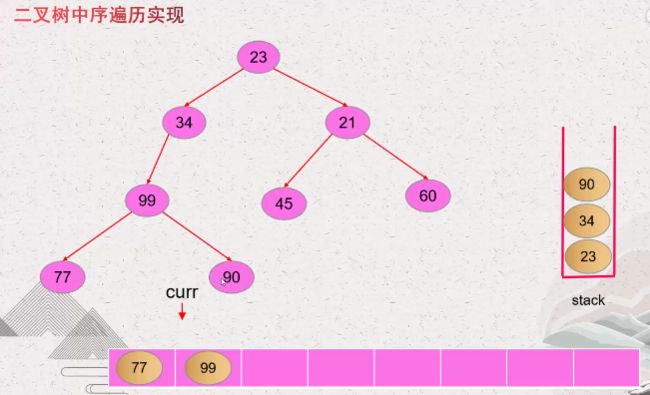
    如果以90为根节点的右子树有左子节点，那么方法同上，依次访问下去
    如果没有左子节点，那么取出栈中的90这个根节点
    

11. 查询以90为根节点的子树是否有右子树
    
    此时以90为根节点的子树右子树节点为空，那么接下来进一步访问栈中所存的对应根节点元素

12. 继续读取栈顶元素（此时对应34）
    
    此时，以34为根节点的左子树我们已经处理完毕了，34这个根节点也读取了，那么接下来处理34对应的右子树。

13. 读取以34为根节点的右子树
    以34为根节点的右子树为空，那么以34为根节点的子树遍历完毕
    
    接下来继续处理栈中元素

14. 继续读取栈中元素（此时为23）
    
    此时，整颗二叉树的左子树都遍历完成，接下来遍历对应的右子树

15. 遍历右子树根节点（根节点为23对应右子树根节点不为空，可继续遍历，先遍历第一个根节点21，并且压入栈中）
    
    

16. 继续先遍历以21为根节点的左子树，不为空则继续压入栈中（45）
    

17. 继续左移，直到有一个左子树为空
    指向为空时（45的左子节点），开始处理栈顶元素，读取栈顶元素
    
    

18. 查询以45为根节点的左子树是否有右子节点
    若有则推入栈中，查询接下来是否有左子节点
    若无则说明以45为根节点的子树访问完毕，接下来继续处理栈顶元素
    

19. 观察以21为根节点的右子树情况，curr=curr.right
    
    右子树根节点不为空（60），则推入栈中
    

20. 观察以60为根节点的右子树是否还有左右节点
    若有左子节点则继续遍历
    若无左子节点则取出栈顶元素（60），开始遍历右子树。
    若右子节点不为空，则推入栈中继续遍历
    若右子节点为空，且栈为空时，则整个中序遍历结束
    

2.2 代码实现

代码前面的说明直接拷贝了力扣的内容，函数的主要思想是
从根节点遍历二叉树，如果根节点为空，则直接返回空list
接下来是正常流程（整个流程走完同上面的遍历过程）

1. 新建两个list，一个作为栈存储栈顶元素，一个存储最终的遍历结果
2. curr开始指向根节点
3. 遍历的结束条件是当前指针为空并且栈中没有元素（这里的while循环条件）
4. 将根节点推入栈中，节点指针左移
5. 当左移后的节点指针为空时，说明以该节点为根节点的子树无左子节点，遍历顺序为左根右，那么左为空，中序遍历则直接读取其栈顶元素（根节点的值），指针也指向该根节点，跳出第二个while循环。
6. 查询以上一步中为根节点为子树的右子节点，移动指针，继续重复上述遍历（进到第一个while循环）
7. 直至指针指向为空，且栈中无元素时，结束中序遍历

2.2.1 python

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution(object):
    def inorderTraversal(self, root):
        """
        :type root: TreeNode
        :rtype: List[int]
        """
    
        if not root:
            return []
        res, stack = list(), list()
        curr = root
        while curr or len(stack): # 指针为空且栈中元素为空时结束循环
            while curr: # 当前指针不为空，推入根节点
                stack.append(curr)
                curr = curr.left
            # 左子节点为空，则读取栈顶元素对应的根节点
            node = stack.pop()
            res.append(node.val)
            # 读取右子树
            curr = node.right
        return res

这里给的用例是
输入：[1,null,2,3]
输出：[1,3,2]
这里我打印了最初的根节点：
(TreeNode{val: 1, left: None, right: TreeNode{val: 2, left: TreeNode{val: 3, left: None, right: None}, right: None}}, 'root')

2.2.2 JavaScript

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[]}
 */
var inorderTraversal = function(root) {
    if (!root) return []
    const stack = [], res = []
    let curr = root
    let node
    while (!(!stack.length && !curr)) { // 指针为空且栈中无元素时，结束循环
    // while (stack.length || curr) {
        while (curr) { // 指针不为空
            stack.push(curr)
            curr = curr.left
        }
        node = stack.pop()
        res.push(node.val)
        curr = node.right
    }
    return res
};

3、递归法

3.1 遍历过程

1. 拆分二叉树
   
   主要思想是将一个完整的二叉树，分成左子树、根节点、右子树
   
   进一步继续拆分
   
   当最左边的左子树其左子节点为空则结束递归

2. 进一步从最小的子树依次访问
   

3. 依次进行遍历
   
   中序遍历=中序遍历左子树+根节点+中序遍历右子树

3.2 代码实现

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[]}
 */
var inorderTraversal = function(root) {
    if (!root) return []
    
    const inorder = (node, res) => {
        if (!node) return
        inorder(node.left, res)
        res.push(node.val)
        inorder(node.right, res)
    }

    const res = []
    inorder(root, res)
    return res
};

参考链接

力扣讲解