python之SPC:计算Cpk
目录
1、Ca、Cp和Cpk的理解
2、python计算Cp,Cpk与Pp,Ppk
3、总结
1、Ca、Cp和Cpk的理解
Ca、Cp和Cpk是制程能力指数,它们分别代表制程准确度、制程精密度和制程能力指数。
制程准确度(Ca)反映实际平均值与规格中心值之一致性。对于单边规格,因不存在规格中心,因此不存在Ca;对于双边规格,Ca=(μ-U)/(T/2)。其中μ为均值,U为规格中心,T为规格
制程精密度(Cp)反映规格公差宽度与制程变异宽度之比例。Cp=T/(6σ)
Cpk是Ca及Cp两者的中和反应。Ca反应的是位置关系(集中趋势),Cp反应的是散布关系(离散趋势)。Cpk的计算公式为:Cpk=Cp(1-┃Ca┃)。
2、python计算Cp,Cpk与Pp,Ppk
以下为计算Cpk的代码,数据存在txt文件,两列数据,每行2个数据,以空格间隔,读取数据后作直方图、概率密度图,打印Cpk等值:
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats
def Ca(data, USL, LSL):
"""
:param data: 数据
:param USL: 数据指标上限
:param LSL: 数据指标下限
:return:
"""
u=np.mean(data)
ca=(u-(USL-(USL-LSL)/2))/((USL-LSL)/2)
return ca
def Cp(data, USL, LSL):
"""
:param data: 数据
:param USL: 数据指标上限
:param LSL: 数据指标下限
:return:
"""
# 计算每组的平均值和标准差
sigma = np.std(data)
cp = (USL - LSL) / 6 / sigma
return cp
def Cpk(data, USL, LSL):
"""
:param data: 数据
:param USL: 数据指标上限
:param LSL: 数据指标下限
:return:
"""
return Cp(data, USL, LSL)*(1-np.abs(Ca(data, USL, LSL)))
def Pp(data, USL, LSL):
"""
:param data: 数据
:param USL: 数据指标上限
:param LSL: 数据指标下限
:return:
"""
sigma = np.std(data)
pp = (USL - LSL) / 6 / sigma
return pp
def Ppk(data, USL, LSL):
"""
:param data: 数据
:param USL: 数据指标上限
:param LSL: 数据指标下限
:return:
"""
u = np.mean(data)
sigma = np.std(data)
ppk = min(USL - u, u - LSL) / 3 / sigma
return ppk
def openreadtxt(file_name):
data = []
with open(file_name, 'r') as file:
file_data = file.readlines() # 读取所有行
for row in file_data:
tmp_list = row.split()
tmp = [float(x) for x in tmp_list]
data.append(tmp) # 将每行数据插入data中
return data
#轮廓点存储路径
filename1 =r"C:\Users\user\Documents\F1-21\cpk.txt"
data = openreadtxt(filename1)
shank_diameter = np.array(data)[:, 0]
# shank_roundness = np.array(data)[:, 1]
usl=3.1715
lsl=3.1685
cp = Cp(shank_diameter, usl, lsl)
cpk = Cpk(shank_diameter, usl, lsl)
pp = Pp(shank_diameter,usl, lsl)
ppk = Ppk(shank_diameter,usl, lsl)
# usl=0.0004
# lsl=0.0
# cp = Cp(shank_roundness, usl, lsl)
# cpk = Cpk(shank_roundness, usl, lsl)
# pp = Pp(shank_roundness,usl, lsl)
# ppk = Ppk(shank_roundness,usl, lsl)
print("Cp=", cp, "Cpk=", cpk, "Pp=", pp, "Ppk=", ppk)
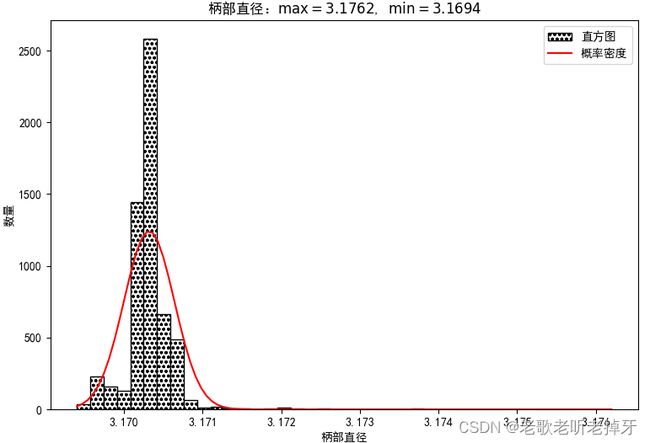
num_bins = 40
plt.figure(figsize=(9,6), dpi=100)
n, bins, patches = plt.hist(shank_diameter, num_bins,color='w', edgecolor='k',hatch=r'ooo',density=1,label="直方图")
x = np.linspace(min(shank_diameter), max(shank_diameter), 100)
plt.plot(x, stats.norm.pdf(x, np.mean(shank_diameter), np.std(shank_diameter)), 'r',label="概率密度")
# plt.axvline(x=usl, color='red', linestyle='--')
# plt.annotate(f'x={usl}', xy=(usl, 2500), xytext=(np.max(shank_roundness)/2,2500),arrowprops=dict(facecolor='green', shrink=0.05))
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.xlabel('柄部直径')
plt.ylabel('数量')
plt.title(f'柄部直径:$\max={np.max(shank_diameter)}$, $\min={np.min(shank_diameter)}$')
plt.legend()
plt.show()
3、总结
1)Cpk计算要求过程稳定,也就是要服从正态分布,本例通过直方图与概率密度图大致判断。
2)所有数据只分一组的话,Cp,Cpk分别与Pp,Ppk相等,那么,数据该分组吗?
3)少量数据偏离规格,偏离越多越远,Cpk越小,但是偏离较远的也可能是异常值,到底该如何区分较远的偏离值与异常值。