算法练习-二分法 LeetCode 74. 搜索二维矩阵

今日感受：⛽️⛽️

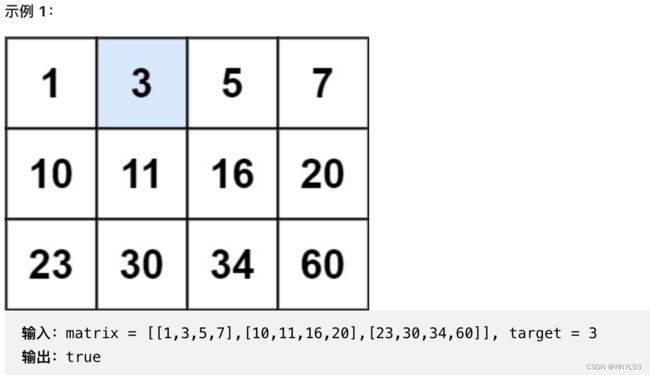
题目描述：

LeetCode 74. 搜索二维矩阵

编写一个高效的算法来判断 m x n 矩阵中，是否存在一个目标值。该矩阵具有如下特性：

每行中的整数从左到右按升序排列。每行的第一个整数大于前一行的最后一个整数。

 解题代码：

class Solution {

    /** 
        二分法进行搜索
    */

    public boolean searchMatrix(int[][] matrix, int target) {

        //获取行列数
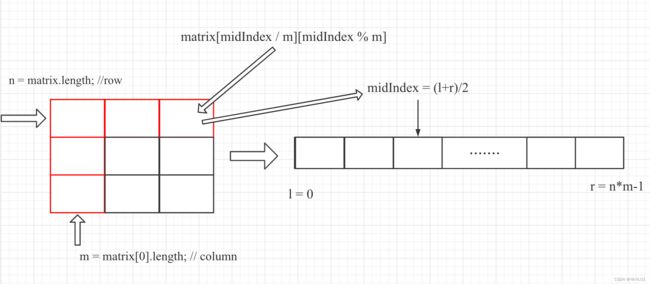
        int n = matrix.length; //row 
        int m = matrix[0].length; // column
        //注意首先判断matrix是否行为0或者列为0
        if(n == 0 || m == 0){
            return false;
        }
        //确定边界
        int l = 0, r = n*m-1;
        //二分搜索
        while(l= target){
                r = midIndex;
            }else{
                l = midIndex + 1;
            }
        }

        if(matrix[r/m][r%m] == target){
            return true;
        }
        // System.out.println(m);
        return false;
    }
}

解题思路：

（1）二维矩阵展开属于单调递增: 对二维矩阵进行展开成一维

---

（2） 确定边界 l = 0, r = n*m-1; 以及循环条件 while(l

---

（3） 确定边界更新条件 ：

        matrix[row][col]>= target 更新 r = midIndex;

        matrix[row][col]< target 更新  l = midIndex + 1; (取所有可能存在的闭区间)

---

（4）结束循环（l == r），判断找到的唯一的点是否与target相等，是return true， 否则return false。

---

小结：

        感觉二分法的套路差不多都是这样：

        （1）确定边界条件

        （2）循环条件

        （3）确定边界更新条件

        （4）找到的唯一值是否与target值相等

        需要注意的是边界更新条件以及是向右逼近（向上取整）还是向左逼近（向下取整）的问题。