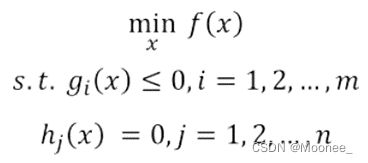机器学习——支持向量机

一、定义

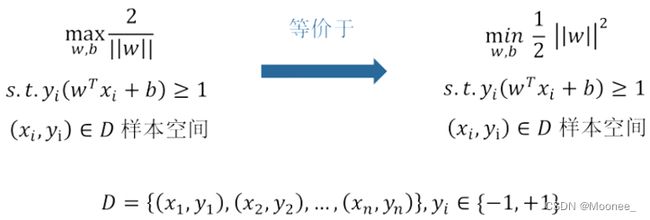
支持向量机（support vector machine，SVM），通俗来讲，它是一种二分类模型，其基本模型定义为特征空间上的间隔最大的线性分类器，其学习策略便是间隔最大化，最终可转化为一个凸二次规划问题的求解。

支持向量机思想直观，但细节复杂，涵盖凸优化，核函数，拉格朗日算子等理论。

二、基本概念

1.线性可分

对于一个数据集合可以画一条直线将两组数据点分开，这样的数据称为线性可分（linearly separable）。见下图：

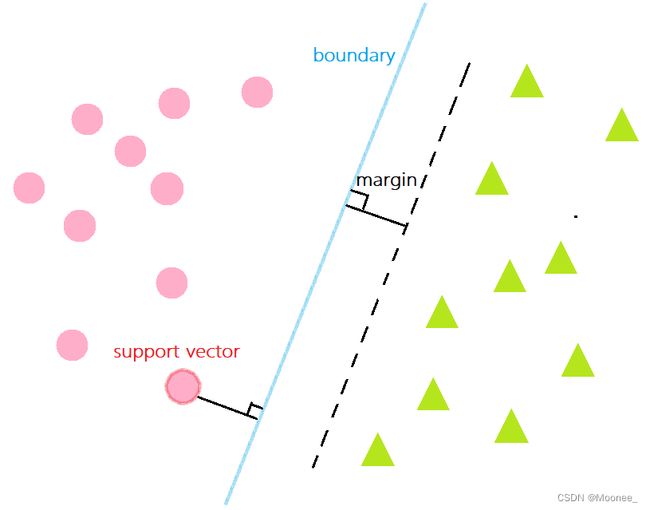
2.分割超平面

将上述数据集分隔开来的直线成为分隔超平面。对于二维平面来说，分隔超平面就是一条直线。

3.超平面

对于三维及三维以上的数据来说，分隔数据的是个平面，称为超平面，也就是分类的决策边界。

4.点相对于分割面的间隔

点到分割面的距离，称为点相对于分割面的间隔。

5.间隔

数据集所有点到分隔面的最小间隔的2倍，称为分类器或数据集的间隔。论文中提到的间隔多指这个间隔。SVM分类器就是要找最大的数据集间隔。

6.支持向量

离分隔超平面最近的那些点。

三、寻找最大间隔

1.分隔超平面

二维空间一条直线的方程为，y=ax+b，推广到n维空间，就变成了超平面方程，即
　　
w是权重，b是截距，训练数据就是训练得到权重和截距。

2.如何决定最好的参数

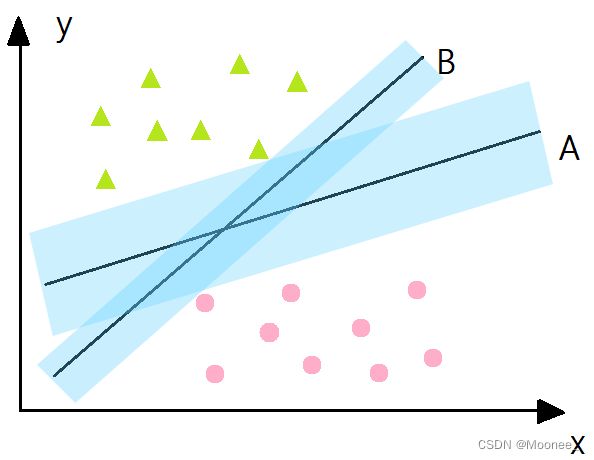
支持向量机的核心思想： 最大间隔化， 最不受到噪声的干扰。如上图所示，分类器A比分类器B的间隔（蓝色阴影）大。

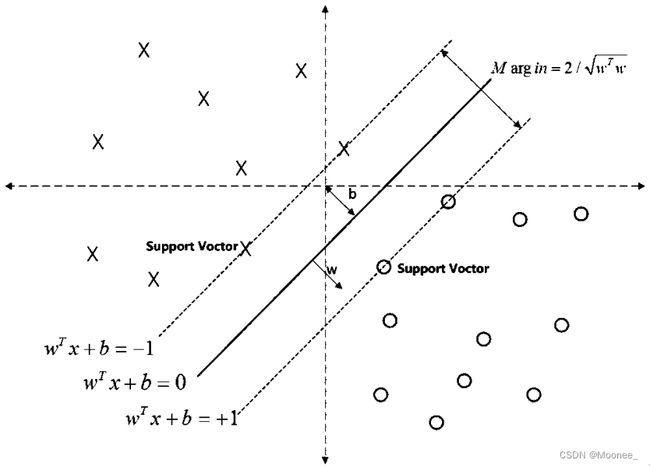
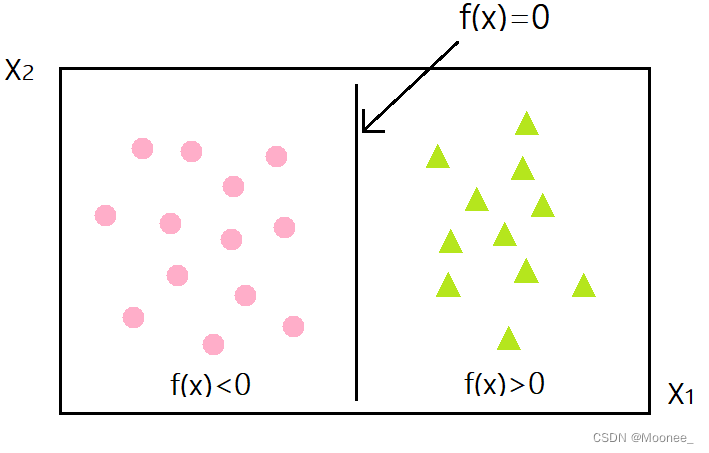
SVM划分的超平面：f(x) = 0，w为法向量，决定超平面方向，
假设超平面将样本正确划分
　　f(x) ≥ 1，y = +1
　　f(x) ≤ −1，y = −1
间隔：r=2/|w|

约束条件：

3.凸优化

设 f(x) 为定义在n维欧式空间中某个凸集 S 上的函数，若对于任何实数α（0 < α< 1 ）以及 S 中的不同两点 x，y ，均有：

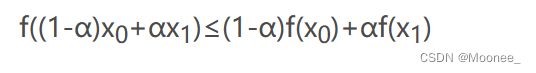
那么，f(x)为定义在凸集 S 上的凸函数。

有约束的凸优化问题：

如果f(x)，g(x)为凸函数，h(x)为仿射函数时，这是一个凸优化的问题。
对于支持向量机：

SVM是一个凸二次规划问题，有最优解。

4.拉格朗日对偶

通常我们需要求解的最优化问题有如下几类：

(i) 无约束优化问题，可以写为：

min f(x)

(ii) 有等式约束的优化问题，可以写为：

min f(x),

s.t. h_i(x) = 0；i =1, …, n

(iii) 有不等式约束的优化问题，可以写为：

min f(x)，

s.t. g_i(x) <= 0；i =1, …, n

h_j(x) = 0；j =1, …, m
　　对于第(i)类的优化问题，常常使用的方法就是Fermat定理，即使用求取f(x)的导数，然后令其为零，可以求得候选最优值，再在这些候选值中验证；如果是凸函数，可以保证是最优解。

①拉格朗日乘子法与对偶问题

对于第(ii)类的优化问题，常常使用的方法就是拉格朗日乘子法（Lagrange Multiplier) ，即把等式约束h_i(x)用一个系数与f(x)写为一个式子，称为拉格朗日函数，而系数称为拉格朗日乘子。通过拉格朗日函数对各个变量求导，令其为零，可以求得候选值集合，然后验证求得最优值。
例如给定椭球：

求这个椭球的内接长方体的最大体积。
我们将这个转化为条件极值问题，即在条件
下，求f(x,y,z)=8xyz的最大值。
　　首先定义拉格朗日函数F(x)：
然后解变量的偏导方程：

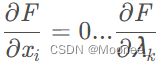
如果有i个约束条件，就应该有i+1个方程。求出的方程组的解就可能是最优化值（极值），将结果带回原方程验证即可得解。

回到上面的题目，通过拉格朗日乘数法将问题转化为：

　　对F(x,y,z,λ)求偏导得：

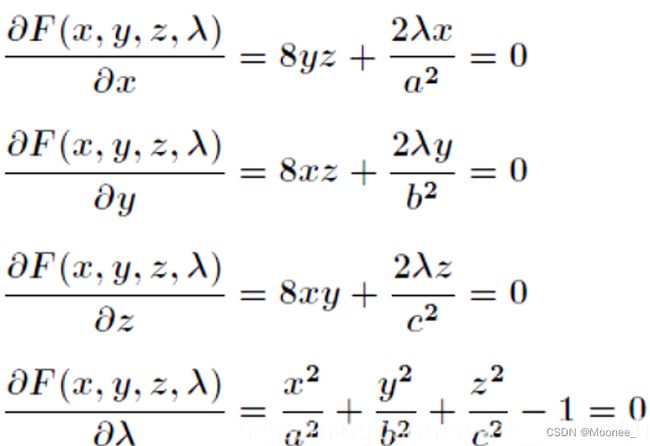
联立前面三个方程得到bx=ay和az=cx，代入第四个方程解得：

最大体积为：

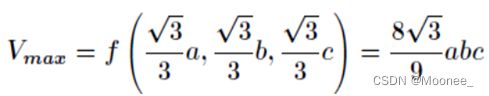
②KKT条件

对于第(iii)类的优化问题，常常使用的方法就是KKT条件（Karush-Kuhn-Tucker）。同样地，我们把所有的等式、不等式约束与f(x)写为一个式子，也叫拉格朗日函数，系数也称拉格朗日乘子，通过一些条件，可以求出最优值的必要条件，这个条件称为KKT条件。

原始含有不等式约束问题描述为：

min f(x)，

s.t. g(x)≤0
含有不等式约束的KKT条件为如下式（记为式①）所示：

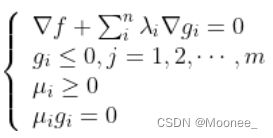
（注意：KKT条件是非线性规划最优解的必要条件）

KKT条件描述型理解
（i）当最优解 x* 满足g(x*) <0时，最优解位于可行域内部，此时不等式约束无效，λ=0。

（ii）当最优解 x满足g(x) = 0时，最优解位于可行域的边界，此时不等式约束变为等式约束，g(x)=0。

（iii）同时根据几何意义，λ必<0（根据梯度可得）。

根据上述讨论，由于我们所需的是必要条件，故将上述几种情况进行并集操作，可得最优解时的必要条件，即（记为式②）：
　　　　　　　　　　　　　　　　∇xL=∇f+λ∇g=0

g(x)≤0

λ≥0

λg(x)=0

（iv）当有多个不等式约束时，可推广至式①形式。

总结：
　　KKT条件要求强对偶，形式如下：
　　
　　前两条为x满足的原问题的约束。第三条表示对偶变量满足的约束，第四条为互补松弛条件，第五条表示拉格朗日函数在x*处取得极小值（即x是最优解，满足拉格朗日函数极小的条件）。

四、核函数

在实际中，我们会经常遇到线性不可分的样例，此时，我们的常用做法是把样例特征映射到高维空间中去，但如果凡是遇到线性不可分的样例，一律映射到高维空间，那么这个维度大小是会高到可怕的，此时就需要使用核函数。核函数虽然也是将特征进行从低维到高维的转换，但核函数会先在低维上进行计算，而将实质上的分类效果表现在高维上，避免了直接在高维空间中的复杂计算。

如下图所示的两类数据，分别分布为两个圆圈的形状，这样的数据本身就是线性不可分的，此时该如何将两类数据分开？
　
上图所述的这个数据集，是用两个半径不同的圆圈加上了少量的噪音生成得到的，所以，一个理想的分界应该是一个“圆圈”而不是一条线（超平面）。

将二维平面的坐标值映射一个三维空间中：下图即是映射之后的结果，将坐标轴经过适当的旋转，就可以很明显地看出，数据是可以通过一个平面来分开的。

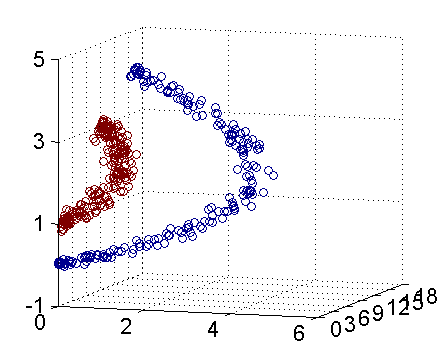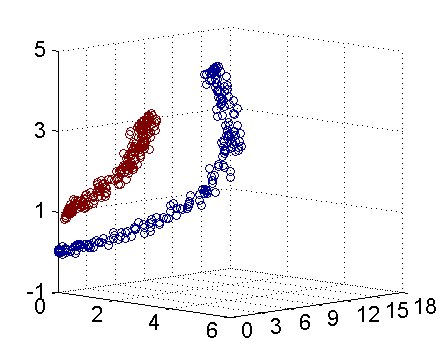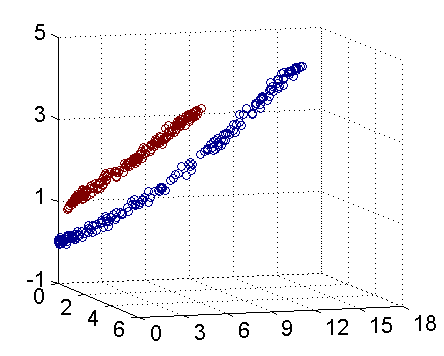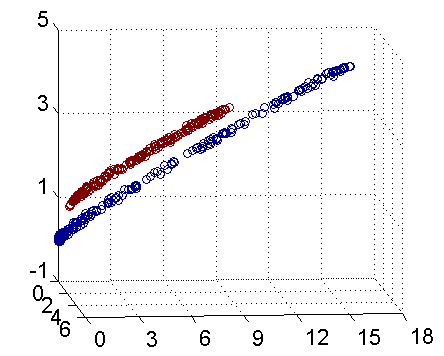
核函数方法处理非线性问题的基本思想：按一定的规则进行映射，使得原来的数据在新的空间中变成线性可分的，从而就能使用之前推导的线性分类算法进行处理。

计算两个向量在隐式映射过后的空间中的内积的函数叫做核函数（这里不详细说明具体的推导计算过程了，比较复杂…）

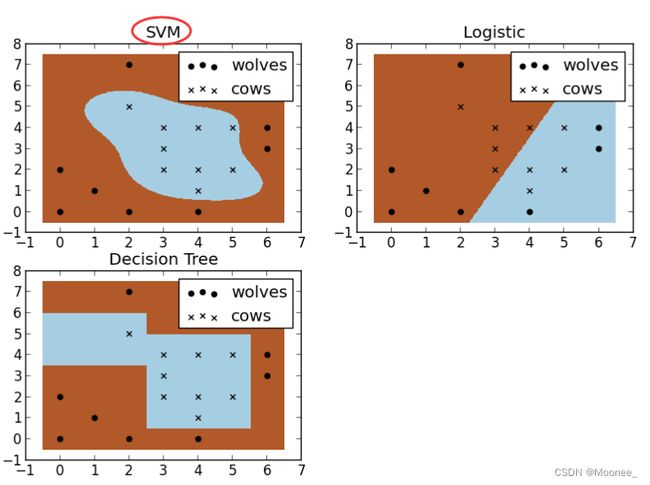
核函数解决非线性问题的直观效果（与决策树、logistic回归比较）：
假设现在你是一个农场主，圈养了一批牛群，但为预防狼群袭击牛群，你需要搭建一个篱笆来把牛群围起来。但是篱笆应该建在哪里呢？你很可能需要依据牛群和狼群的位置建立一个“分类器”，比较下图这几种不同的分类器，我们可以看到SVM完成了一个很完美的解决方案。

这个例子从侧面简单说明了SVM使用非线性分类器的优势，而logistic模式以及决策树模式都是使用了直线方法。

五、正则化与软间隔

针对样本不是完全能够划分开的情况，可以允许支持向量机在一些样本上出错，为此要引入“软间隔”的概念。

引入正则化强度参数C（正则化：在一定程度上抑制过拟合，使模型获得抗噪声能力，提升模型对未知样本的预测性能的手段），损失函数重新定义为：

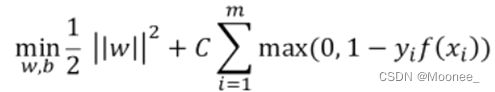
上式为采用hinge损失的形式，再引入松弛变量ξi≥0，重写为：

支持向量：

由此可以看出，软间隔支持向量机的最终模型仅与支持向量有关，即通过采用hinge损失函数仍保持了稀疏特性。

六、SMO算法

1.优化目标函数和约束条件

经过拉格朗日乘子法得到的优化目标函数为：

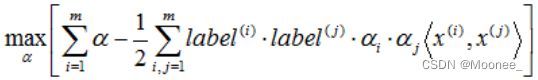
约束条件为：

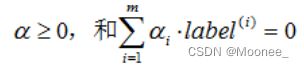
但是，对于上述目标函数，是存在一个假设的，即数据100%线性可分。但我们知道几乎所有数据都不那么"干净"。这时可以通过引入松弛变量(slack variable)，来允许有些数据点可以处于超平面的错误的一侧。这样我们的优化目标就能保持仍然不变，但是此时约束条件为：

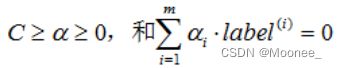
2.Platt的SMO算法

1996年，John Platt发布了一个称为SMO的强大算法，用于训练SVM。

SMO表示序列最小化(Sequential Minimal Optimizaion)。Platt的SMO算法是将大优化问题分解为多个小优化问题来求解的。这些小优化问题往往很容易求解，并且对它们进行顺序求解的结果与将它们作为整体来求解的结果完全一致的。在结果完全相同的同时，SMO算法的求解时间短很多。

SMO算法的目标是求出一系列alpha和b，一旦求出了这些alpha，就很容易计算出权重向量w并得到分隔超平面。

SMO算法的工作原理是：每次循环中选择两个alpha进行优化处理。一旦找到了一对合适的alpha，那么就增大其中一个同时减小另一个。

这里所谓的"合适"就是指两个alpha必须符合以下两个条件，条件之一就是两个alpha必须要在间隔边界之外，而且第二个条件则是这两个alpha还没有进进行过区间化处理或者不在边界上。

3.简化版SMO

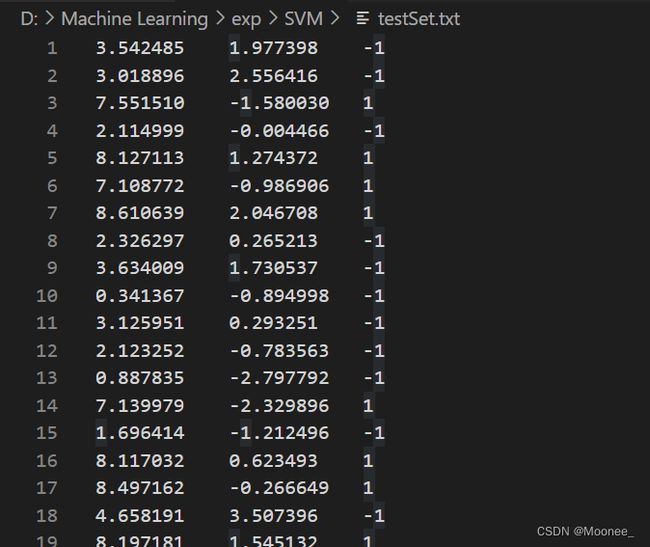
①数据集准备

②辅助函数

首先在数据集上遍历每一个alpha , 然后在剩下的alpha集合中随机选择另一个alpha,从而构建alpha对。这里有一点相当重要，就是我们要同时改变两个alpha 。若是改变一个，约束条件中的第二个可能会失效。

def loadDataSet(fileName):#打开文件并逐行解析
    dataMat = []; labelMat = []
    fr = open(fileName)
    for line in fr.readlines():                                     
        lineArr = line.strip().split('\t')
        dataMat.append([float(lineArr[0]), float(lineArr[1])]) #添加数据
        labelMat.append(float(lineArr[2]))                      #添加标签
    return dataMat,labelMat

#辅助函数1，随机选择一个整数
def selectJrand(i, m):#i是alpha下标，m是alpha个数
    j = i                                 
    while (j == i):
        j = int(random.uniform(0, m))
    return j


#辅助函数2，调整大于H或小于L的alpha值
def clipAlpha(aj,H,L):
    if aj > H:
        aj = H
    if L > aj:
        aj = L
    return aj
dataArr,labelArr=loadDataSet('testSet.txt')
labelArr

运行结果：

SMO函数伪代码：

创建一个alpha向量并将其初始化为0向量
当迭代次数小于最大迭代次数时（外循环） :
     对数据集中的每个数据向量（内循环）：
     如果该数据向量可以被优化：
         随机选择另一个数据向量
         同时优化这两个向量
         如果两个向量都不能被优化，退出内循环
    如果所有向量都没被优化，增加迭代次数，继续下一次循环

def smoSimple(dataMatIn, classLabels, C, toler, maxIter):#dataMatIn数据集, classLabels类别标签, C常数, toler容错率, maxIter最大循环次数
    #转换为numpy的mat存储
    dataMatrix =np. mat(dataMatIn); labelMat = np.mat(classLabels).transpose()
    #初始化b，m，n为dataMatrix的维度
    b = 0; m,n = np.shape(dataMatrix)
    #初始化alpha参数，设为0
    alphas = np.mat(np.zeros((m,1)))
    #初始化迭代次数
    iter = 0
   
    #最多迭代matIter次
    while (iter < maxIter):
        alphaPairsChanged = 0
        
        for i in range(m):
            #计算误差Ei
            fXi = float(np.multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[i,:].T)) + b
            Ei = fXi - float(labelMat[i])
            #优化alpha
            if ((labelMat[i]*Ei < -toler) and (alphas[i] < C)) or ((labelMat[i]*Ei > toler) and (alphas[i] > 0)):
                #使用辅助函数1随机选择另一个alpha
                j = selectJrand(i,m)
                #计算误差Ej
                fXj = float(np.multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[j,:].T)) + b
                Ej = fXj - float(labelMat[j])
            #保存更新前的aplpha值，使用copy
                alphaIold = alphas[i].copy(); alphaJold = alphas[j].copy();
               
            #计算L和H
                if (labelMat[i] != labelMat[j]):
                    L = max(0, alphas[j] - alphas[i])
                    H = min(C, C + alphas[j] - alphas[i])
                else:
                    L = max(0, alphas[j] + alphas[i] - C)
                    H = min(C, alphas[j] + alphas[i])
                if L==H: print("L==H"); continue
                
                #计算最优修改量eta,
                eta = 2.0 * dataMatrix[i,:]*dataMatrix[j,:].T - dataMatrix[i,:]*dataMatrix[i,:].T - dataMatrix[j,:]*dataMatrix[j,:].T
                if eta >= 0: print("eta>=0"); continue
               
            #alpha_j
                alphas[j] -= labelMat[j]*(Ei - Ej)/eta
                
                #使用辅助函数2调整alpha j
                alphas[j] = clipAlpha(alphas[j],H,L)
                if (abs(alphas[j] - alphaJold) < 0.00001): print("j not moving enough"); continue
                
                #改变alpha_i
                alphas[i] += labelMat[j]*labelMat[i]*(alphaJold - alphas[j])
                
                #更新b1和b2
                b1 = b - Ei- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[i,:].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[i,:]*dataMatrix[j,:].T
                b2 = b - Ej- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[j,:].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[j,:]*dataMatrix[j,:].T
                
                #根据b1和b2更新b
                if (0 < alphas[i]) and (C > alphas[i]): b = b1
                elif (0 < alphas[j]) and (C > alphas[j]): b = b2
                else: b = (b1 + b2)/2.0
                
                #统计优化次数
                alphaPairsChanged += 1
                
                #打印统计信息
                print("iter:%d i:%d ,pairs changed %d" % (iter,i,alphaPairsChanged))
        
        #更新迭代次数
        if (alphaPairsChanged == 0): iter += 1
        else: iter = 0
        print("iteratuin number: %d" % iter)
    return b,alphas
b,alphas=smoSimple(dataArr, labelArr, 0.6, 0.001,40)

运行结果：

b
alphas[alphas>0]
np.shape(alphas[alphas>0])
for i in range(100):
    if alphas[i]>0.0:print (dataArr[i],labelArr[i])

③对支持向量画圈

def showClassifer(dataArr, w, b):
    #绘制样本点
    data_1 = [];data_2 = []
    for i in range(len(dataArr)):
        if labelArr[i] > 0:
            data_1.append(dataArr[i])
        else:
            data_2.append(dataArr[i])
    data_1_np = np.array(data_1)              #转换为numpy矩阵
    data_2_np = np.array(data_2)            #转换为numpy矩阵
    plt.scatter(np.transpose(data_1_np)[0], np.transpose(data_1_np)[1], s=30, alpha=0.7,c='blueviolet')   #正样本散点图
    plt.scatter(np.transpose(data_2_np)[0], np.transpose(data_2_np)[1], s=30, alpha=0.7,c='pink') #负样本散点图
    #绘制直线
    x1 = max(dataArr)[0]
    x2 = min(dataArr)[0]
    a1, a2 = w
    b = float(b)
    a1 = float(a1[0])
    a2 = float(a2[0])
    y1, y2 = (-b- a1*x1)/a2, (-b - a1*x2)/a2
    plt.plot([x1, x2], [y1, y2])
    #找出支持向量点
    for i, alpha in enumerate(alphas):
        if abs(alpha) > 0:
            x, y = dataArr[i]
            plt.scatter([x], [y], s=150, c='none', alpha=0.7, linewidth=1.5, edgecolor='red')
    plt.title('cxr_test')
    plt.show()


def get_w(dataArr, labelArr, alphas):
    alphas, dataArr, labelArr = np.array(alphas), np.array(dataArr), np.array(labelArr)
    w = np.dot((np.tile(labelArr.reshape(1, -1).T, (1, 2)) * dataArr).T, alphas)
    return w.tolist()

w = get_w(dataArr, labelArr, alphas)
showClassifer(dataArr, w, b)

4.完整版SMO

##Platt SMO的支持函数
class optStruct:
    def __init__(self,dataMatIn, classLabels, C, toler):
        self.X = dataMatIn
        self.labelMat = classLabels
        self.C = C
        self.tol = toler
        self.m = np.shape(dataMatIn)[0]
        self.alphas = np.mat(np.zeros((self.m,1)))
        self.b = 0
        self.eCache = np.mat(np.zeros((self.m,2)))

def calcEk(oS, k):#计算e并返回
    fXk = float(np.multiply(oS.alphas,oS.labelMat).T*(oS.X*oS.X[k,:].T)) + oS.b
    Ek = fXk - float(oS.labelMat[k])
    return Ek

def selectJ(i, oS, Ei):#选择第二个alpha
    maxK = -1; maxDeltaE = 0; Ej = 0
    oS.eCache[i] = [1,Ei]
    validEcacheList = np.nonzero(oS.eCache[:,0].A)[0]#构建一个非零表
    if (len(validEcacheList)) > 1:
        for k in validEcacheList:
            if k == i: continue
            Ek = calcEk(oS, k)
            deltaE = abs(Ei - Ek)
            if (deltaE > maxDeltaE):
                maxK = k; maxDeltaE = deltaE; Ej = Ek
        return maxK, Ej
    else:
        j = selectJrand(i, oS.m)
        Ej = calcEk(oS, j)
    return j, Ej

def updateEk(oS, k):#计算误差值并返回缓存中
    Ek = calcEk(oS, k)
    oS.eCache[k] = [1,Ek]


##Platt SMO的优化历程
def innerL(i, oS):
    Ei = calcEk(oS, i)
    if ((oS.labelMat[i]*Ei < -oS.tol) and (oS.alphas[i] < oS.C)) or ((oS.labelMat[i]*Ei > oS.tol) and (oS.alphas[i] > 0)):
        j,Ej = selectJ(i, oS, Ei)
        alphaIold = oS.alphas[i].copy(); alphaJold = oS.alphas[j].copy();
        if (oS.labelMat[i] != oS.labelMat[j]):
            L = max(0, oS.alphas[j] - oS.alphas[i])
            H = min(oS.C, oS.C + oS.alphas[j] - oS.alphas[i])
        else:
            L = max(0, oS.alphas[j] + oS.alphas[i] - oS.C)
            H = min(oS.C, oS.alphas[j] + oS.alphas[i])

        if L==H: print("L==H"); return 0
        eta = 2.0 * oS.X[i,:]*oS.X[j,:].T - oS.X[i,:]*oS.X[i,:].T - oS.X[j,:]*oS.X[j,:].T

        if eta >= 0: print("eta>=0"); return 0
        oS.alphas[j] -= oS.labelMat[j]*(Ei - Ej)/eta
        oS.alphas[j] = clipAlpha(oS.alphas[j],H,L)
        updateEk(oS, j)

        if (abs(oS.alphas[j] - alphaJold) < 0.00001): print("j not moving enough"); return 0
        oS.alphas[i] += oS.labelMat[j]*oS.labelMat[i]*(alphaJold - oS.alphas[j])
        updateEk(oS, i)

        b1 = oS.b - Ei- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.X[i,:]*oS.X[i,:].T - oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.X[i,:]*oS.X[j,:].T
        b2 = oS.b - Ej- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.X[i,:]*oS.X[j,:].T - oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.X[j,:]*oS.X[j,:].T

        if (0 < oS.alphas[i]) and (oS.C > oS.alphas[i]): oS.b = b1
        elif (0 < oS.alphas[j]) and (oS.C > oS.alphas[j]): oS.b = b2
        else: oS.b = (b1 + b2)/2.0
        return 1
    else: return 0


##Platt SMO的外循环代码
def smoP(dataMatIn, classLabels, C, toler, maxIter,kTup=('lin', 0)):
    oS = optStruct(np.mat(dataMatIn),np.mat(classLabels).transpose(),C,toler)
    iter = 0
    entireSet = True; alphaPairsChanged = 0

    #如果迭代字数大于最大迭代数，或者遍历完整个集合还没有找到一对i和j可以优化，那么退出迭代
    while (iter < maxIter) and ((alphaPairsChanged > 0) or (entireSet)):
        alphaPairsChanged = 0
        if entireSet:   #遍历所有的值
            for i in range(oS.m):
                alphaPairsChanged += innerL(i,oS)  #innerL第二个选择alpha
                print("fullSet, iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged))
            iter += 1
        else:#遍历非边界值
            nonBoundIs = np.nonzero((oS.alphas.A > 0) * (oS.alphas.A < C))[0]
            for i in nonBoundIs:
                alphaPairsChanged += innerL(i,oS)
                print("non-bound, iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged))
            iter += 1

        if entireSet: entireSet = False
        elif (alphaPairsChanged == 0): entireSet = True
        print("iteration number: %d" % iter)
    return oS.b,oS.alphas

运行效果：

dataArr,labelArr=loadDataSet('testSet.txt')
b,alphas=smoP(dataArr,labelArr,0.6,0.001,40)

实现分类：

def calcWs(alphas,dataArr,classLabels):
    X = np.mat(dataArr); labelMat = np.mat(classLabels).transpose()
    m,n = np.shape(X)
    w = np.zeros((n,1))
    for i in range(m):
        w += np.multiply(alphas[i]*labelMat[i],X[i,:].T)
    return w
ws=calcWs(alphas,dataArr,labelArr)
ws

datMat=np.mat(dataArr)

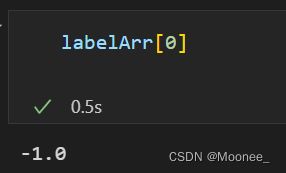
datMat[0]*np.mat(ws)+b

得到的值大于0属于1类，小于0属于-1类。
对于数据点0，根据上述结果，类别标签为-1，根据下面的命令确认一下：

图像显示：

与简化版的不同，完整版SMO算法选出的支持向量样点更多，更接近理想的分隔超平面。对比两种算法的运算时间，完整版SMO算法的速度比简化版SMO算法的速度快很多。

（但是选择出的样点好像有点错误…）

七、基于SVM的手写数字识别

设置属性防止中文乱码：

rcParams['font.sans-serif'] = [u'SimHei']
mpl.rcParams['axes.unicode_minus'] = False
#加载数字图片数据
digits = datasets.load_digits()
digits

获取样本数量，并将图片数据格式化（要求所有图片的大小、像素点都是一致的 => 转换成为的向量大小是一致的）

n_samples = len(digits.images)
data = digits.images.reshape((n_samples, -1))
data.shape

模型构建：

classifier = svm.SVC(gamma=0.001)#默认是rbf
#使用二分之一的数据进行模型训练
#取前一半数据训练，后一半数据测试
classifier.fit(data[:int(n_samples / 2)], digits.target[:int(n_samples / 2)])

测试数据部分实际值和预测值获取：

#后一半数据作为测试集
expected = digits.target[int(n_samples/2):] ##y_test
predicted = classifier.predict(data[int(n_samples / 2):])##y_predicted
#计算准确率
print("分类器%s的分类效果:\n%s\n"
      % (classifier, metrics.classification_report(expected, predicted)))
#生成一个分类报告classification_report
print("混淆矩阵为:\n%s" % metrics.confusion_matrix(expected, predicted))
#生成混淆矩阵
print("score_svm:\n%f" %classifier.score(data[int(n_samples / 2):], digits.target[int(n_samples / 2):]))

进行图片展示：

plt.figure(facecolor='gray', figsize=(12,5))
#先画出5个预测失败的
#把预测错的值的 x值 y值 和y的预测值取出
images_and_predictions = list(zip(digits.images[int(n_samples / 2):][expected != predicted], expected[expected != predicted], predicted[expected != predicted]))
#通过enumerate，分别拿出x值 y值 和y的预测值的前五个，并画图
for index,(image,expection, prediction) in enumerate(images_and_predictions[:5]):
    plt.subplot(2, 5, index + 1)
    plt.axis('off')                          
    plt.imshow(image, cmap=plt.cm.gray_r, interpolation='nearest')#把cmap中的灰度值与image矩阵对应，并填充
    plt.title(u'预测值/实际值:%i/%i' % (prediction, expection))
#再画出5个预测成功的
images_and_predictions = list(zip(digits.images[int(n_samples / 2):][expected == predicted], expected[expected == predicted], predicted[expected == predicted]))
for index, (image,expection, prediction) in enumerate(images_and_predictions[:5]):
    plt.subplot(2, 5, index + 6)
    plt.imshow(image, cmap=plt.cm.gray_r, interpolation='nearest')
    plt.title(u'预测值/实际值:%i/%i' % (prediction, expection))

plt.subplots_adjust(.04, .02, .97, .94, .09, .2)
plt.show()