数据结构之二叉树OJ(C++)
根据二叉树创建字符串
606. 根据二叉树创建字符串 - 力扣（LeetCode）
题目的要求是给我们一棵二叉树,让我们用前序遍历的方式把它转换成一个由整数和括号组成的字符串。
我们观察它给的用例会发现其实整数就是每个结点的值,括号其实是把每棵树的左右子树括起来。另外还要求省略掉不必要的空括号对，但是又不能无脑的全部省略掉，省略后不能影响字符串与原始二叉树之间的一对一映射关系。
所以我们可以先来分析一下，哪些情况需要省略空括号，哪些情况不能省略
那对照着图我们很容易得出，括号的处理应该是这样的：1.根结点不为空的情况对应子树的括号肯定不省略
2.左不为空，左子树的括号一定不省略3.左为空
3.1 右不为空, 左子树的括号不能省略
3.2 右也为空, 左子树的括号省略
4. 右为空, 右子树的括号省略
class Solution {
public:
string tree2str(TreeNode* root)
{
string ret;
if(root == nullptr)
return ret;
ret += to_string(root->val);//左不省略括号的两种情况,1是左不为空,2是左为空右不为空
if(root->left || root->right)
{
ret += '(';
ret += tree2str(root->left);
ret += ')';
}
if(root->right)//右为空就省略
{
ret += '(';
ret += tree2str(root->right);
ret += ')';
}
return ret;
}
};二叉树的层序遍历
题目：link
层序遍历之前讲过：
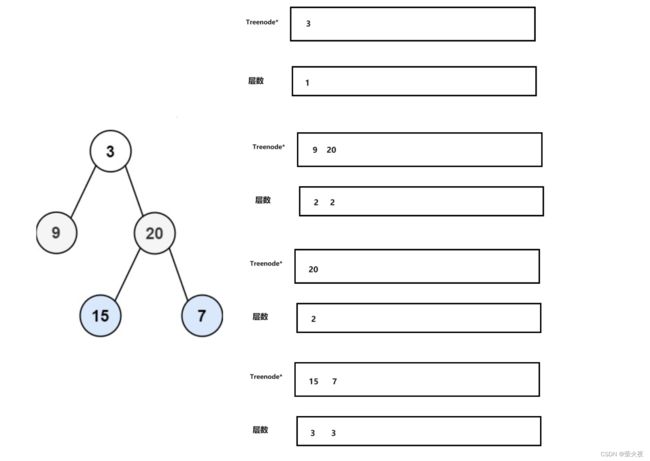
借助一个队列就可以搞, 先让根结点入队列,然后如果队列不为空,就出对头数据, 并把对头数据的孩子结点带入队列,然后继续出对头数据,再将其孩子带入队列,依次循环往复,直到队列为空,就遍历完成了。最终出队列的顺序就是层序遍历的顺序。
题目中要求我们把层序遍历的结果放到一个二维数组里面返回，二维数组里面每一个放到是一层的遍历结果 , 所以这道题的关键是如何控制把每一层的遍历结果放在不同的数组里面，最后放到一个二维数组里面。
我们再增加一个变量levelsize设为1，去记录每一层结点的个数，每出一个，就
- -一次，一层出完，此时队列中的元素个数就是下一层的结点个数, 重新为levelsize赋值,继续进行下一层的遍历, 这样确保每一层的结点能放到不同的数组中。
class Solution {
public:
vector> levelOrder(TreeNode* root)
{
int levelsize;
vector> vv;
if(!root)
return vv;
queue q;
if(root != nullptr)
{
q.push(root);
levelsize = 1;
}
while(levelsize)
{
vector v;
while(levelsize--)
{
auto node = q.front();
q.pop();
v.push_back(node->val);
if(node->left)
q.push(node->left);
if(node->right)
q.push(node->right);
}
levelsize = q.size();
vv.push_back(v);
}
return vv;
}
}; 另一种思路我们可以借助两个队列来搞：
一个队列就是去放结点的指针，利用队列的先进先出，上一层带下一层，完成二叉树的层序遍历。另外一个队列用来存放对应结点的层数，比如根结点入队列时存一个1，根结点出去把他的孩子带进队列，带进几个孩子，就存几个2（上一层的层数+1）
那这样我们就能区分不同结点的层数，从而把不同层的结点按照层序遍历的顺序放到不同的是数组里面。
二叉树的层序遍历 II
在上一题的基础上把得到的二维的vector逆置一下就行了。
reverse(vv.begin(),vv.end());class Solution {
public:
vector> levelOrderBottom(TreeNode* root)
{
int levelsize;
vector> vv;
if(!root)
return vv;
queue q;
if(root != nullptr)
{
q.push(root);
levelsize = 1;
}
while(levelsize)
{
vector v;
while(levelsize--)
{
auto node = q.front();
q.pop();
v.push_back(node->val);
if(node->left)
q.push(node->left);
if(node->right)
q.push(node->right);
}
levelsize = q.size();
vv.push_back(v);
}
int left = 0, right = vv.size()-1;
reverse(vv.begin(),vv.end());
return vv;
}
}; 二叉树最近公共祖先
236. 二叉树的最近公共祖先 - 力扣（LeetCode）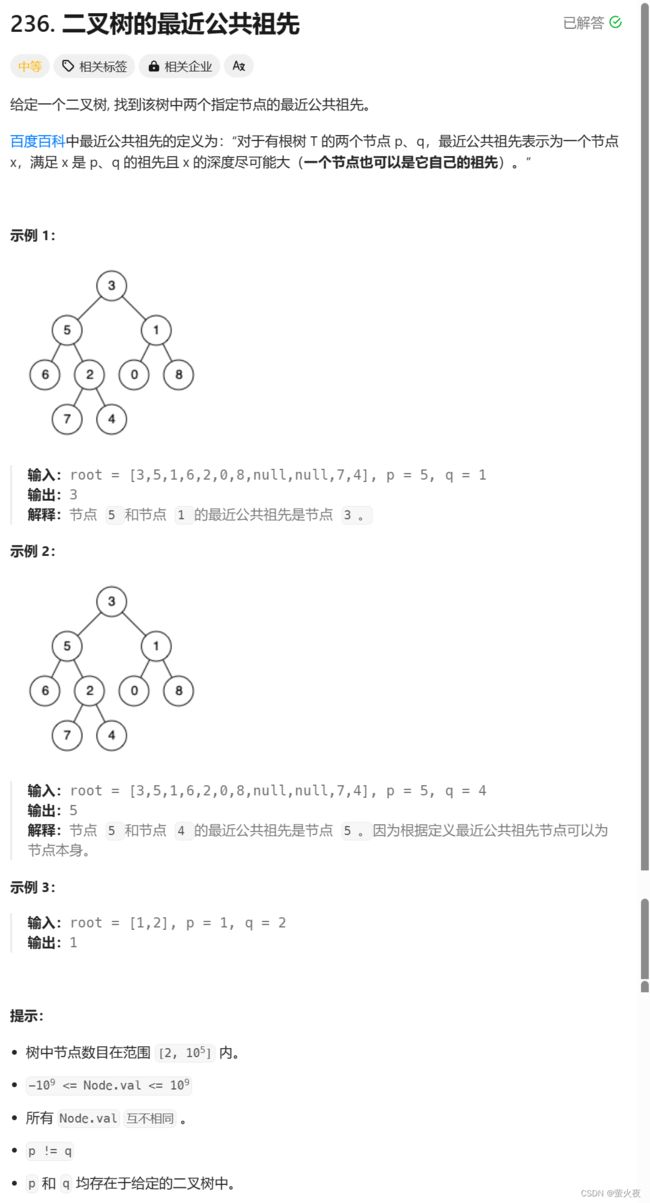
思路1（转换为链表相交问题）
当前二叉树的结构只有左右孩子两个指针,
但如果它是一个三叉链的结构,还有一个指向父结点的指针:
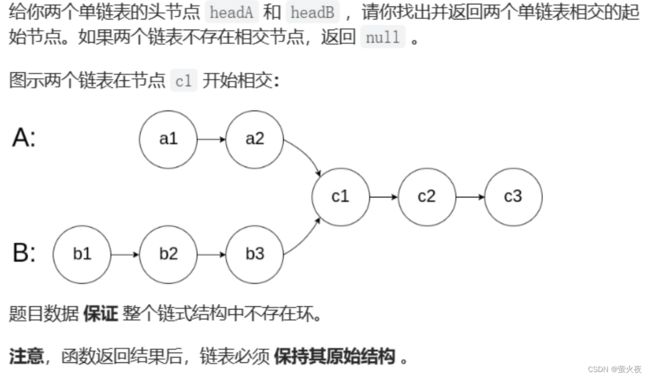
那这道题就可以看作一个链表相交的问题了:
有了parent指针我们就可以从孩子结点沿着parent往上走了，就像链表从前完后走一样。
链表相交问题
法一: 可以让A链表的每个结点依次与B中的结点比较, 找到就返回相交的结点, 找不到就返回空,但是这样效率太低.
法二:
1.首先遍历两个链表找尾, 判断两个链表的尾结点是否相同, 不相同, 那就肯定不相交, 直接返回空
2.如果相交的话,去找相交点,先计算出两个链表长度的差值gap, 然后让长的那个链表先走gap步, 走完gap步之后两链表此时的长度就相等了两两相对应, 然后两个链表一块走, 每走一步. 判断两个结点是否相同, 第一个相同的结点就是第一个交点。
思路2
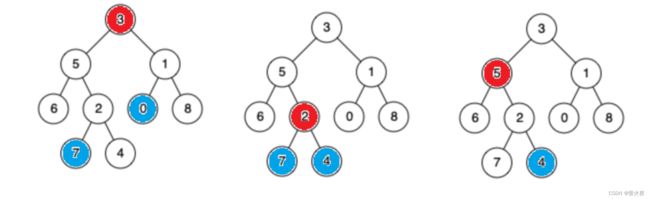
以三种情况为例:
第一种情况, 要查找的两个结点一个在整棵树根结点的左子树上, 一个在右子树上, 所以根结点就是它们最近的公共祖先。
第二种情况, 两个结点都在根结点的同一颗子树上, 那根结点不会是最近的公共祖先了, 其次, 公共结点有可能在右子树吗？不可能, 所以我们就可以递归去左子树查找, 那后续也是一样, 到了左子树发现两个结点都在5结点的右子树上, 所以再递归到右子树查找, 那此时就走到了2的位置, 找到了最近公共祖先第三种情况首先还是会递归到左子树, 然后走到5这个结点, 会发现一个结点时5本身, 另一个结点在5的右子树, 所以5就是最近公共祖先。因此我们得出一个结论, 如果两个结点里面有一个是某棵树的根结点, 另一个在这棵树的子树上，那么这个根结点就是最近公共祖先。
代码思路就是先从根结点开始判断, 判断两个结点是否分别在根结点的左右子树, 如果是就直接返回根结点, 如果不是两个结点要么都在左子树要么都在右子树, 递归root->left或root->right继续查找, 如果查找到其中的一个结点是根结点, 就返回这个结点(情况3).
class Solution {
public:
//判断结点是否在root为根的树中
bool exist(TreeNode* root, TreeNode* node)
{
//root为空查找失败
if(root == nullptr)
return false;
//查找成功
if(root == node)
return true;
//继续在左右子树中查找
return exist(root->left,node) || exist(root->right,node);
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q)
{
if(root == nullptr)
return nullptr;
bool leftp = exist(root->left,p);//判断p是否在左子树
bool rightp = !leftp;//判断p是否在右子树
bool leftq = exist(root->left,q);//判断q是否在左子树
bool rightq = !leftq;//判断q是否在右子树
if(root == p || root == q)
return root;
if(leftp && rightq || leftq && rightp)
{
return root;
}
else if(leftp && leftq)
return lowestCommonAncestor(root->left,p,q);
else
return lowestCommonAncestor(root->right,p,q);
}
};这种方法其实效率是比较低的, 它的时间复杂度是O(N^2)
首先我们从根节点不断往左右子树去递归的过程是一个O(N), 然后每一次递归去判断在不在的过程也是一个O(N), 所以是O(N^2)
优化:转化为路径相交的问题
首先我们可以获取从根结点开始到两个结点的路径, 然后保存到容器里面, 那选择什么容器保存路径呢？
这里用栈（stack）是比较合适的（先进后出）
从根结点开始，首先判断根结点不为空, 为空直接返回false, 不为空先把根结点入栈, 然后判断根结点是不是目标结点, 是的话, 直接返回true, 栈里面的根结点就是路径, 不是的话, 就去左子树找。
左子树重复上述步骤, 找到了返回true没找到返回false, 然后去右子树找. 如果都没找到的话说明要找的结点不在当前子树, 就pop, 返回false, 然后递归回上一层继续找.
这个找路径这个算法时间复杂度是是O(N),获取了路径,之后的步骤就跟链表相交找交点类似, 先让元素多的那个栈出元素, 出到两个栈元素个数一样的时候, 同时出数据, 然后遇到第一个相同的元素,就是最近的公共祖先。所以该算法整体就是一个O(N)的算法, 当然代价是额外开了两个栈。
class Solution {
public:
bool getPath(TreeNode* root,TreeNode* node, stack& s)
{
if(root == nullptr)
return false;
s.push(root);
if(s.top() == node)
return true;
if(getPath(root->left,node,s))
return true;
if(getPath(root->right,node,s))
return true;
s.pop();
return false;
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q)
{
stack sp;
stack sq;
getPath(root,p,sp);
getPath(root,q,sq);
while(sp.size() != sq.size())
{
if(sp.size() > sq.size())
sp.pop();
else
sq.pop();
}
while(sp.top() != sq.top())
{
sp.pop();
sq.pop();
}
return sp.top();
}
}; 二叉搜索树与双向链表
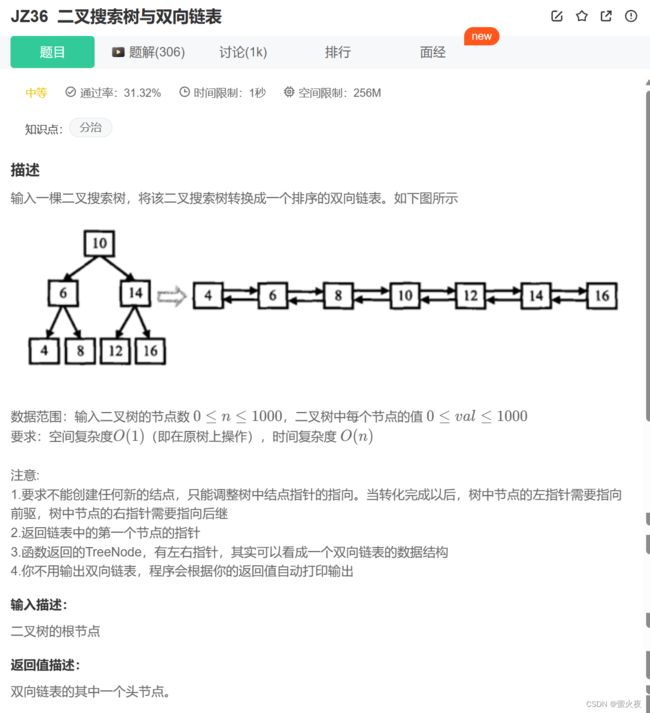
二叉搜索树与双向链表_牛客题霸_牛客网 (nowcoder.com)
题目给我们一个搜索二叉树, 要求我们转换为一个排序的双向链表, 并作出了以下要求:
1.要求不能创建任何新的结点, 只能调整树中结点指针的指向, 当转化完成以后, 树中节点的左指针需要指向前驱, 树中节点的右指针需要指向后继.(第一条很关键, 这决定着空间复杂度为1)
2.返回链表中的第一个节点的指针
3.函数返回的TreeNode, 有左右指针, 其实可以看成一个双向链表的数据结构
4.你不用输出双向链表, 程序会根据你的返回值自动打印输出
5.空间复杂度O(1)（即在原树上操作）,时间复杂度 O(n)
思路1:
一种比较简单的方法是, 我们可以中序遍历搜索二叉树（中序遍历的结果就是升序）,按照遍历的顺序把所有结点放到一个容器里比如vector就可以, 然后再遍历vector去依次改变指针的指向将它转换成双向链表, 但是题目要求空间复杂度为O(1), 所以不能开辟额外的空间.
思路2:
在原树上进行操作, 在中序遍历的同时直接改变指针的指向, 如果是中序遍历打印的话, 中间这里就是打印结点的值, 而现在我们不是打印值，而是在中间这里改变指针的指向进行链接
那中间这个链接的过程怎么写呢？
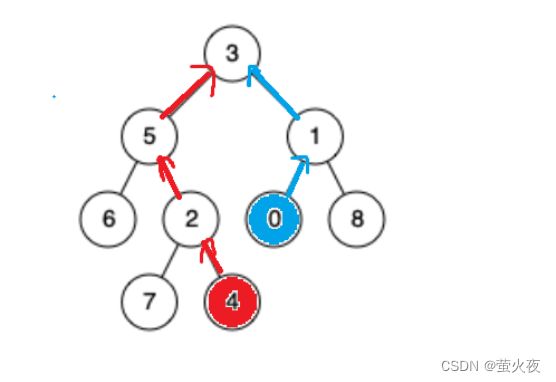
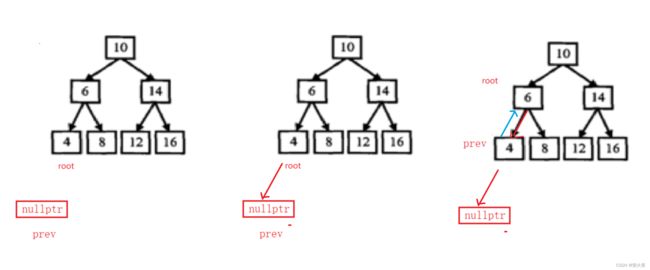
在遍历的过程中当前结点只能去构建它与它的左子树的链接,链接当前结点的前驱和它孩子的后继, 因为此时并不知道它的父结点是谁所以它的后继只能由它的父结点来实现链接, 于是可以记录一下前驱结点prev, prev初始值为空nullptr
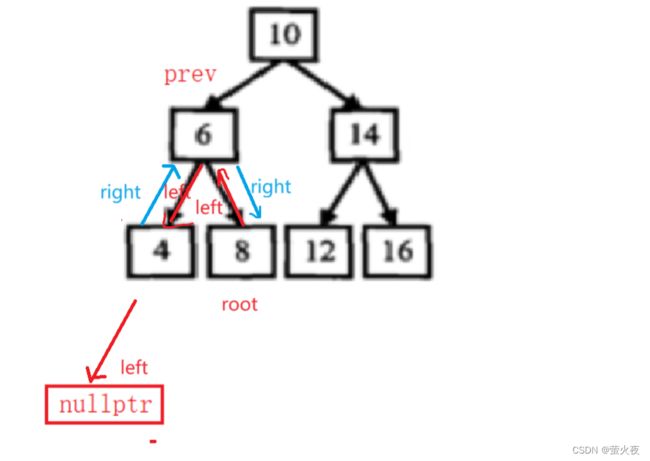
中序遍历的话第一个结点是4, 我们用root记录每次递归的结点, 那此时怎么按照双向链表的形式去链接呢？
我们让root的left指针指向prev, 然后让prev=root,更新一下prev的值, 因为prev的后继还没构建,需要保存记录给上一层进行处理:
class Solution {
public:
void InOrderLink(TreeNode* root,TreeNode*& prev)
{
//root为空不需要链接
if(root == nullptr)
return;
//链接
InOrderLink(root->left,prev);
root->left = prev;
if(prev)//第一次prev为空,为空不需要链接
prev->right = root;
prev = root;
InOrderLink(root->right,prev);
}
TreeNode* Convert(TreeNode* pRootOfTree)
{
//根节点为空直接返回空
if(pRootOfTree == nullptr)
return nullptr;
//找到链表的头结点,也就是二叉搜索树中最小的结点
TreeNode* lefthead = pRootOfTree;
while(lefthead->left)
{
lefthead = lefthead->left;
}
//进行链接
TreeNode* pre = nullptr;
InOrderLink(pRootOfTree,pre);
return lefthead;
}
};
遍历构造
前序与中序遍历序列构造二叉树
105. 从前序与中序遍历序列构造二叉树 - 力扣（LeetCode）
思路:
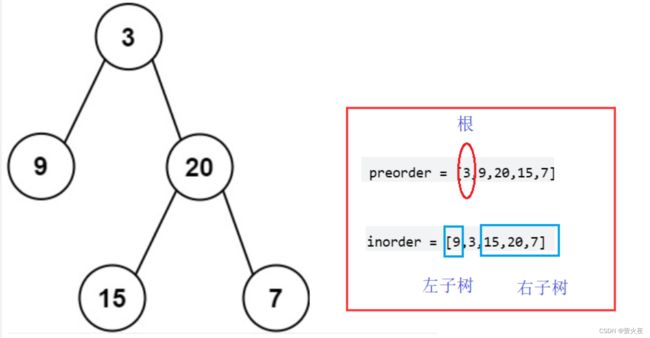
前序序列找根, 前序遍历的第一个结点就是整棵树的根结点, , 然后根据根在中序遍历找左右子树的区间:
那能够确定根结点和左右子树区间, 我们就可以走一个前序递归去创建这棵树了, 首先构建根结点, 然后再根据左右子树区间去递归构建左子树和右子树, 左右子树递归的时候, 同样划分为根和左右子树分别进行处理, 最后把构建好的左右子树链接到根结点上就好了。
class Solution {
public:
TreeNode* build(vector& preorder, vector& inorder,int& prei, int begin,int end)
{
//创建根节点
int rootval = preorder[prei++];
TreeNode* node = new TreeNode(rootval);
//划分区间,在中序中找到根,然后划分出左右子树区间
int mid;
for(int i = begin; i < end; i++)
{
if(rootval == inorder[i])
{
mid = i;
break;
}
}
//[begin,mid-1][mid+1,end]
int begin1 = begin;
int end1 = mid-1;
int begin2 = mid+1;
int end2 = end;
//如果区间存在就继续递归构建子树,不存在就说明它的左/右子树为空,不需要构建
if(begin1 <= end1)
node->left = build(preorder,inorder,prei,begin1,end1);
if(begin2 <= end2)
node->right = build(preorder,inorder,prei,begin2,end2);
return node;
}
TreeNode* buildTree(vector& preorder, vector& inorder)
{
int prei = 0;//prei用来记录创建到哪个根节点
TreeNode* root = build(preorder,inorder,prei,0,inorder.size()-1);
return root;
}
}; 注意：
prei是遍历前序序列的下标，而区间是根据中序序列划分的区间。在递归过程中，我们是拿到对应的由中序序列确定的子树区间，然后按照当前子树对应的前序遍历的顺序构建的。
中序与后序遍历序列构造二叉树
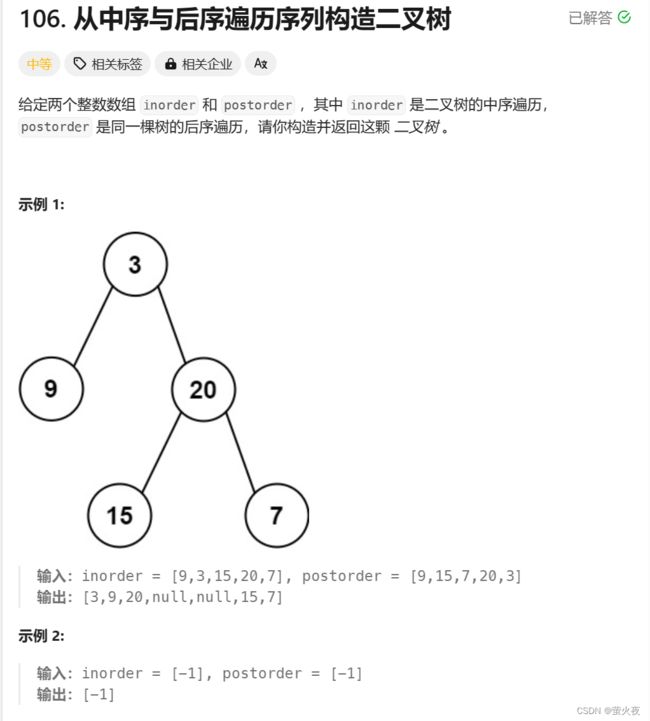同上题类似, 在后序遍历的数组找根, 在中序遍历的数组找左右子树区间, 需要注意的是:
1.后序遍历是左子树 右子树 根, 所以要从后往前找根.
2.构建的时候要先构建右子树再构建左子树, 因为posti这个下标是依次递减的按照顺序进行构建的, 而postorder中一个根的前一个值一定是它的右子树的根, 按照顺序需要先构建右子树.
补充: 由于前序遍历是根 左子树 右子树, preorder中根的下一个位置的值一定是它的左子树的根, 所以需要先构建左子树再构建右子树.
class Solution {
public:
TreeNode* build(vector& inorder, vector& postorder,int& posti, int begin, int end)
{
//区间不存在就返回空
if(begin > end)
return nullptr;
//创建根节点
int rootval = postorder[posti--];
TreeNode* root = new TreeNode(rootval);
//划分左右子树的区间
int mid;
for(int i = begin; i < end ;i++)
{
if(inorder[i] == rootval)
{
mid = i;
break;
}
}
int begin2 = mid+1;
int end2 = end;
int begin1 = begin;
int end1 = mid-1;
//构造左右子树
root->right = build(inorder,postorder,posti,begin2,end2);
root->left = build(inorder,postorder,posti,begin1,end1);
return root;
}
TreeNode* buildTree(vector& inorder, vector& postorder)
{
int posti = postorder.size()-1;
TreeNode* root = build(inorder,postorder,posti,0,inorder.size()-1);
return root;
}
}; 遍历
二叉树的前序遍历(非递归)
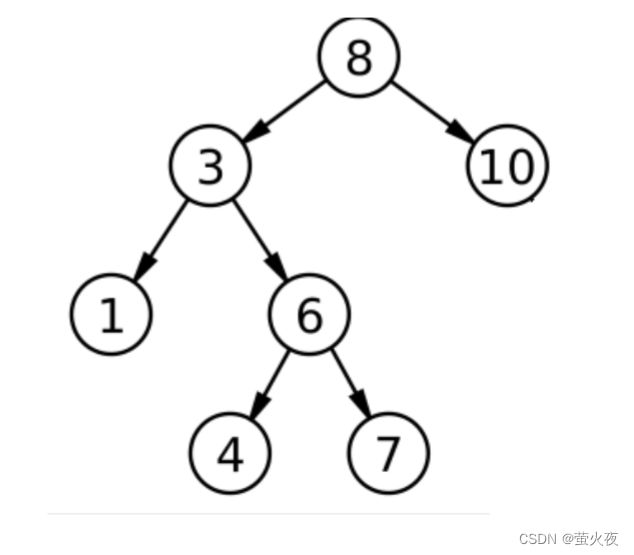
前序遍历是根、左子树、右子树, 所以首先从根结点开始, 顺着访问左子树: 8、3、1
然后现在还有谁没访问？1的右子树、3的右子树，和8的右子树, 所以下面倒着访问1、3、8的右子树就行了.
所以非递归的前序遍历是这样处理的：
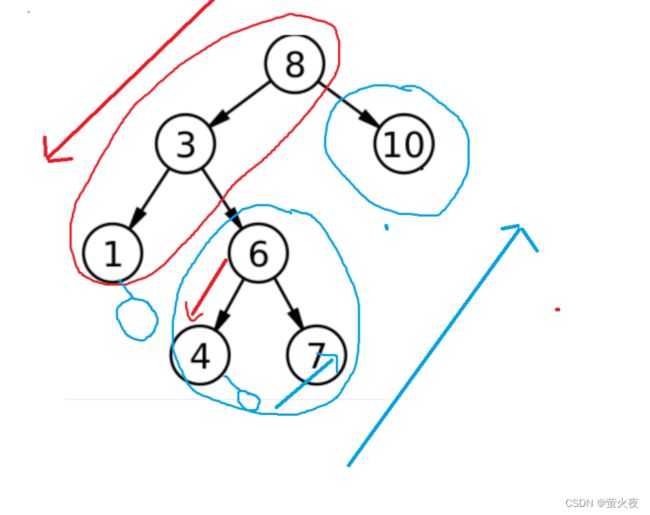
把一棵二叉树分为两个部分：
左路结点
左路结点的右子树对于每一棵左子树，也是同样划分为这两个部分进行处理。
如何倒着去处理左路结点的右子树？
此时我们就可以借助一个栈来搞
以这棵树为例，从根结点8开始，依次访问左路结点8，3，1。
在访问过程中除了将他们放到要返回的vector里面，再把左路结点放到栈里面
class Solution {
public:
vector preorderTraversal(TreeNode* root)
{
stack s;
vector ret;
TreeNode* node = root;
//直到node为空且栈为空,整棵树才遍历完
while(node || !s.empty() )
{
//先从左路遍历一棵树
while(node)
{
s.push(node);
ret.push_back(node->val);
node = node->left;
}
//出了while循坏代表左路已经遍历完
//此时栈里的结点都是右路还没遍历的
node = s.top();
s.pop();
//node变成右子树的根接着上去遍历
node = node->right;
}
return ret;
}
}; 二叉树的中序遍历(非递归)
94. 二叉树的中序遍历 - 力扣（LeetCode）
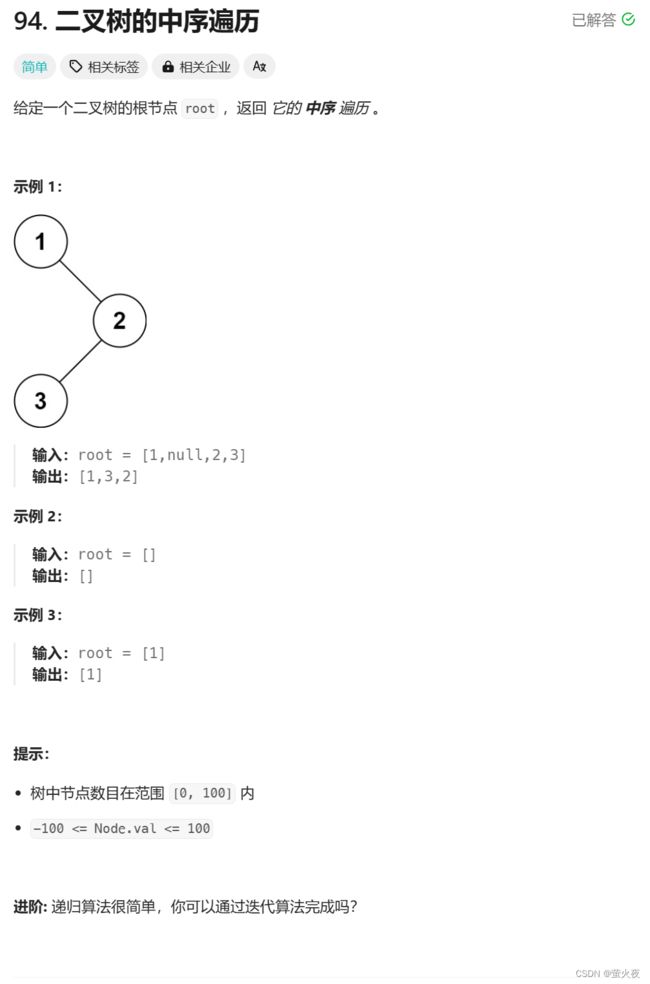中序和前序类似, 只需要调整向vector中插入元素的顺序:
中序是先访问左子树，然后再访问根
所以我们先把左路结点入栈，但是不放进vector里面。一直走到1的左子树为空然后停止入栈, 那这时就可以认为1的左子树是空已经遍历过了, 然后出栈里面的元素(从栈里面取出一个左路结点的时候, 就意味着它的左子树已经访问过了), 第一个出的是1, 那此时遇到1我们要把它放到vector, 因为1的左子树访问过后, 就要访问根了（左子树、根、右子树）
class Solution {
public:
vector inorderTraversal(TreeNode* root)
{
stack s;
vector ret;
TreeNode* node = root;
while(node || !s.empty())
{
while(node)
{
s.push(node);
node = node->left;
}
node = s.top();
s.pop();
ret.push_back(node->val);
node = node->right;
}
return ret;
}
}; 二叉树的后序遍历(非递归)
145. 二叉树的后序遍历 - 力扣（LeetCode）
后序遍历前面的操作和中序是一样的：还是让左路结点先入栈, 但是此时对于栈顶的元素我们不可以直接让它入vector然后pop掉, 中序我们是这样做的, 因为从栈里面取出一个左路结点的时候, 就意味着它的左子树已经访问过了, 然后中序的话该访问根了, 而把栈顶元素放到vector里面然后pop掉就相当于访问根结点。
但是我们后序就不能直接这样了, 因为后序要在右子树访问完之后再去访问根, 此时就需要判断右子树是不是空, 是空的话就可以直接出栈插入, 不是的话要继续访问右子树.
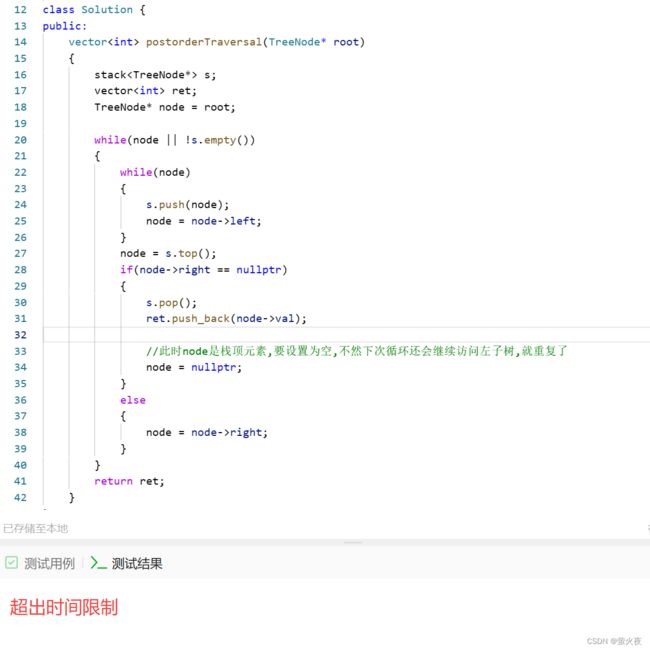
但此时会发现超出了时间限制, 原因在于:
此时我们访问到7了, 7的右子树为空直接pop插入没问题:
此时我们node第二次回到了6这个结点处, 此时的6是左右子树都访问完了, 应该要pop插入了, 但是按照if条件又会继续重复访问右子树, 构成死循环.
怎么解决?
再添加一个prev结点, 每次保存上一次pop出去的结点, 如果node的右子树等于prev, 那就说明右子树已经遍历完了, 可以继续访问根节点了.
class Solution {
public:
vector postorderTraversal(TreeNode* root)
{
stack s;
vector ret;
TreeNode* node = root;
TreeNode* prev = nullptr;
while(node || !s.empty())
{
while(node)
{
s.push(node);
node = node->left;
}
node = s.top();
if(node->right == nullptr || node->right == prev)
{
s.pop();
ret.push_back(node->val);
prev = node;
node = nullptr;
}
else
{
node = node->right;
}
}
return ret;
}
};