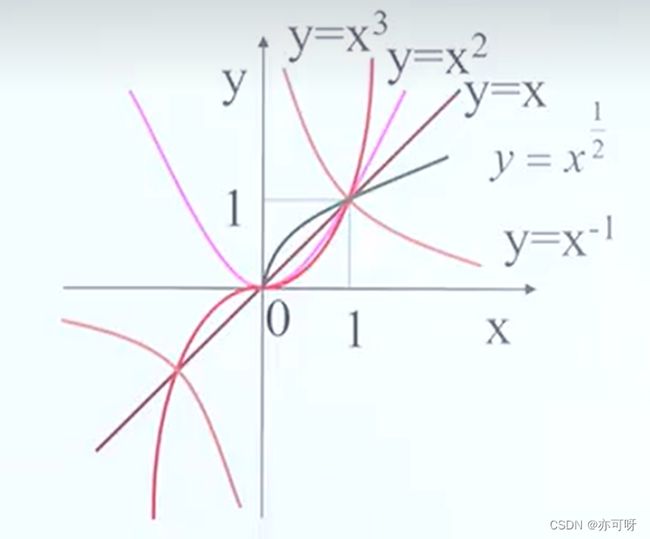高等数学(预备知识之幂函数)

一.什么是幂函数

幂函数 y=x^a (a为常数, x为自变量)

例题1: 判断下列是否为幂函数
(1) y=x⁴

(2) y=2x²

(3) y=2x

(4) y=x³+2

(5) y=-x²

只有第一个是对的, 严格意义上来讲,自变量前面不能有前缀和后缀
\quad
\quad

二.幂函数的函数图像及性质

性质:
(1): 图像都过(1,1)点

(2): y=x^a
(a>1或 a<0) 当a为奇数时,y为奇函数, 当a为偶数时, y为偶函数
(0

(3): y=0 为即奇又偶函数

(4): y=x^-1 中x不能为0, 因为分母不能为0

(5): y=x^a 在第一象限内, 当a>0时是增函数, 当a<0时是减函数

(6): 在第一象限内, y=x^-1的图像与x,y轴无限接近
\quad
\quad

三.常见题型

例题2: 设a$\in$ {-1, 1, $\frac{1}{2}$, 3},则使函数y=x^a的定义域是R,且为奇函数的所有a的值是____
答案: 1, 3

解析:
y=x^-1 中x不能为0
y= $\sqrt{x}$ 取不到负

例题3: 比较下列各组数的大小

例题4:

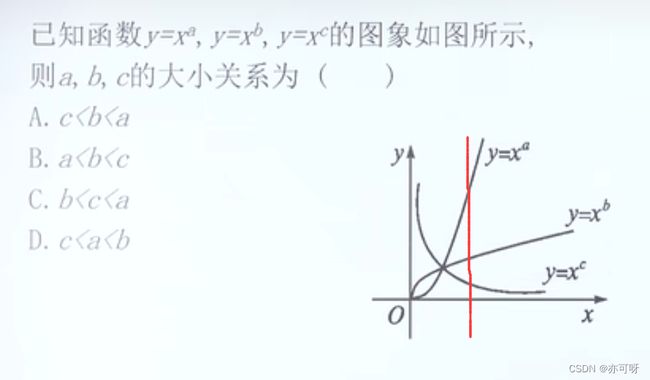
方法一: 在x=1的右边画一条竖线,在上面的大
方法二: a>1, 0 \quad
\quad

四.常见的函数模型

(1) 一次函数模型: f(x)=kx+b (k,b为常数, k≠0)

(2) 反比例函数模型: f(x)=$\frac{k}{x}$ + b (k,b为常数, k≠0)

(3) 二次函数模型: f(x)=ax²$\pm$bx +c (a,b,c为常数, a≠0)

(4)幂函数模型: f(x)=axⁿ+b (a,b,n为常数, a≠0, n≠1)
\quad
\quad

五.n次方根

(1):如果xⁿ=a, 那么x叫做a的n次方根, (其中n>1, n为正整数)
n次方根的个数
1.当n是奇数时
2.当n是偶数时, 分为x>0和x<0两种情况

(2):式子 $\sqrt[n]{a}$ 叫做根式, 这里n叫做根指数, a叫做被开方数

性质(n>1且为自然数):
($\sqrt[n]{a}$)ⁿ = a

$\sqrt[n]{a^n}$ : 当n为奇数时为a, 当n为偶数时为|a|

例题5:
$\sqrt{a^2}$ = |a|

($\sqrt{a}$)² = a

例题6: m是实数, 则下列式子中可能没有意义的是( C )
A. $\sqrt[4]{m^2}$

B. $\sqrt[5]{m}$

C. $\sqrt[6]{m}$

D. $\sqrt[5]{-m}$

解析: 根指数为奇时, 被开方数才能为负

(3) :
$\sqrt{a}$ 为算术平方根
$\pm$$\sqrt{a}$ 为平方根

例题7: 化简
(1) $\sqrt[n]{(x-\pi {)}^n}$ 其中(x<π, n $\in$ N^*)
当n为奇数时, x-π
当n为偶数时, π-x

(2) $\sqrt[6]{4a^2-4a+1}$ 其中(a $\le$ $\frac{1}{2}$)

$\sqrt[6]{(2a-1{)}^2}$

$\sqrt[3]{|2a-1|}$

$\sqrt[3]{1-2a}$

\quad

六.分数指数幂

$a^{\frac{n}{m}}$ = $\sqrt[m]{a^n}$ \quad (m,n $\in$ Z*)

例如: $a^{\frac{1}{2}}$ = $\sqrt{a}$ \quad $a^{\frac{2}{3}}$ = $\sqrt[3]{a^2}$

例题8: 把根式a$\sqrt{a}$ 化成分数指数幂是
=> a * $a^{\frac{1}{2}}$
=> $a^{\frac{3}{2}}$

例题9:
$\sqrt{a\sqrt{a}}$ => $\sqrt{a\ast a^{\frac{1}{2}}}$ => $\sqrt{a^{\frac{3}{2}}}$ => $a^{\frac{3}{2}}$* $a^{\frac{1}{2}}$ => $a^{\frac{3}{4}}$

\quad

七.无理数指数幂

一般地, 无理数指数幂x^a (a>0, a是无理数) 是一个确定的实数, 有理数指数幂的运算性质同样适用于无理数指数幂

例题10: