归并排序 merge Sort + 图解 + 递归 / 非递归

1. 归并排序(merge sort)的主要思想是：将若干个有序序列逐步归并，最终归并为一个有序序列
2. 二路归并排序(2-way merge sort)是归并排序中最简单的排序方法

（1）二路归并排序的递归实现

// 二路归并排序的递归实现
void merge(vector& arr,int left, int mid, int right) {
	int n = right - left + 1;
	vector help(n, 0);
	int i = 0,a = left, b = mid + 1;
	while (a <= mid && b <= right) {
		help[i++] = arr[a] <= arr[b] ? arr[a++] : arr[b++];
	}	
	while (a <= mid) { // 对第一个子序列进行收尾工作
		help[i++] = arr[a++];
	}
	while (b <= right) { // 对第二个子序列进行收尾工作
		help[i++] = arr[b++];
	}
	for (int i = 0; i < n; i++) {
		arr[i+ left] = help[i];
	}
}

void mergeSort(vector& arr,int left, int right) {
	if (left == right) return;// 只有1个记录，递归结束
	int mid = (left + right) / 2;
	//int mid = left + ((right - left) >> 1);
	mergeSort(arr,left, mid);//归并排序前半个子序列
	mergeSort(arr,mid + 1, right);//归并排序后半个子序列
	merge(arr,left, mid, right);//将两个已排序的子序列合并
}

二路归并排序需要进行 趟，合并两个子序列的时间性能为。因此，二路归并排序的时间复杂度是，这是归并排序算法最好，最坏，平均的时间性能。

二路归并排序在归并过程中需要与待排序序列同样数量的存储空间，空间复杂度为。二路归并排序是一种稳定的排序方法。

总结：归并排序的递归实现是一种自顶向下的方法，形式简洁但效率相对较差。

---

（2）二路归并排序的非递归实现

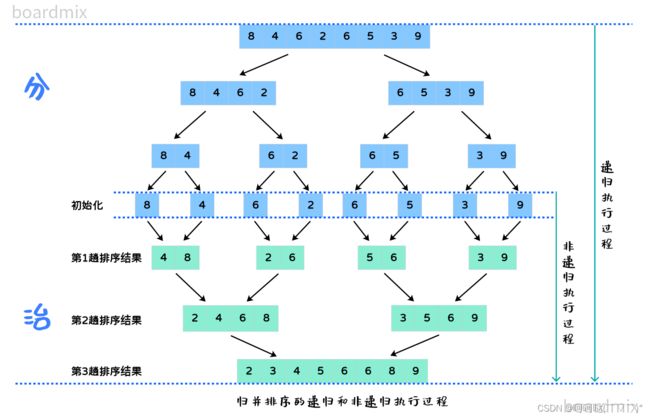
分析二路归并排序的递归执行过程，如图所示，可以将具有 n 个记录的待排序序列看成是 n 个长度为 1 的有序子序列，然后进行两两合并，得到 个长度为 2 的有序子序列（最后一个有序序列的长度可能是1），再进行两两归并，得到 个长度为 4 的有序子序列（最后一个有序序列的长度可能小于4），以此类推，直至得到一个长度为 n 的有序序列

二路归并排序的非递归实现需要解决的关键问题是：

• ① 如何构造初始的有序子序列？
• ② 如何实现有序子序列的两两合并从而完成一趟归并？
• ③ 如何控制二路归并的结束？

问题①的解决：设待排序序列含有 n 个记录，则可将整个序列看成是 n 个长度为 1 的有序子序列

问题②的解决：在一趟归并中，除最后一个有序序列外，其他有序序列中记录的个数（称为序列长度）相同，用 h 表示。现在的任务是把若干个相邻的长度为 h 的有序序列和最后一个长度有可能小于 h 的有序序列进行两两合并，将结果存放到 help[n] 中，为此，设参数 i 指向待归并序列的第一个记录。初始时 i = 0，显然合并的步长应该是 2h。在归并过程中，有以下三种情况：

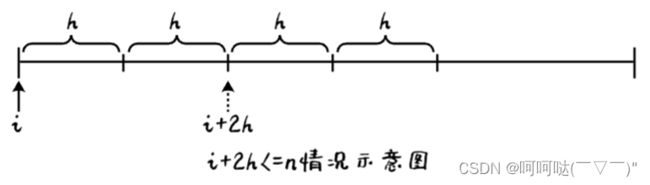
• 情况一：若 i + 2h <= n，表示待合并的两个相邻的有序子序列的长度均为 h ,如下图所示：执行一次合并，完成后 i 加 2h，准备进行下一次合并

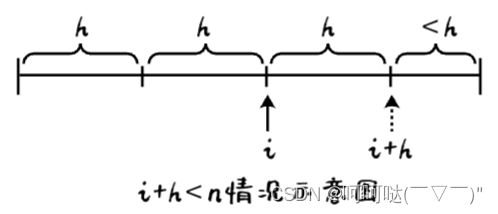
• 情况二：若 i + h < n，则表示仍有两个相邻有序子序列，一个长度为 h ，另一个长度小于 h，如下图所示：执行这两个有序序列的合并，完成后退出一趟归并

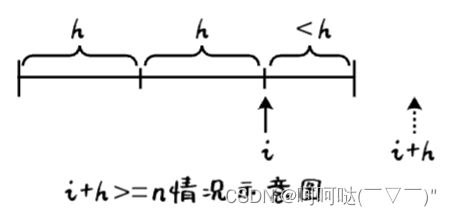
• 情况三：若 i + h >= n，则表明只剩下一个有序子序列，如下图所示，不用合并 

综上，一趟归并排序的成员函数定义如下：

void mergePass(vector& arr,int h,int n) {
	int i = 0;
	while (i + 2 * h <= n) { // 有两个长度为 h 的子序列
		merge(arr,i, i + h - 1, i + 2 * h - 1);
		i = i + 2 * h;
	}
	if (i + h < n) { // 两个子序列一个长度小于h
		merge(arr,i, i + h - 1, n - 1);
	}
}

问题③的解决：开始时，有序子序列的长度为1，结束时，有序子序列的长度为 n。因此，可以用有序子序列的长度来控制排序过程的结束。二路归并排序非递归算法的成员函数定义如下：

void mergeSort2(vector& arr,int n) {
	int h = 1;
	while (h < n) { // 两个子序列一个长度小于h
		mergePass(arr,h, n); // 一趟归并排序
		h = 2 * h;
	}
}

总结：归并排序的非递归实现是一种自底向上的方法，算法效率较高，但算法较为复杂。

---

（3）C++完整代码： 

/*
	归并排序(merge sort)的主要思想是：将若干个有序序列逐步归并，最终归并为一个有序序列
	二路归并排序(2-way merge sort)是归并排序中最简单的排序方法

	we
*/
#include 
#include 
using namespace std;

// 二路归并排序的递归实现
void merge(vector& arr,int left, int mid, int right) {
	int n = right - left + 1;
	vector help(n, 0);
	int i = 0,a = left, b = mid + 1;
	while (a <= mid && b <= right) {
		help[i++] = arr[a] <= arr[b] ? arr[a++] : arr[b++];
	}	
	while (a <= mid) { // 对第一个子序列进行收尾工作
		help[i++] = arr[a++];
	}
	while (b <= right) { // 对第二个子序列进行收尾工作
		help[i++] = arr[b++];
	}
	for (int i = 0; i < n; i++) {
		arr[i+ left] = help[i];
	}
}

void mergeSort(vector& arr,int left, int right) {
	if (left == right) return;// 只有1个记录，递归结束
	int mid = (left + right) / 2;
	//int mid = left + ((right - left) >> 1);
	mergeSort(arr,left, mid);//归并排序前半个子序列
	mergeSort(arr,mid + 1, right);//归并排序后半个子序列
	merge(arr,left, mid, right);//将两个已排序的子序列合并
}

void mergePass(vector& arr,int h,int n) {
	int i = 0;
	while (i + 2 * h <= n) { // 有两个长度为 h 的子序列
		merge(arr,i, i + h - 1, i + 2 * h - 1);
		i = i + 2 * h;
	}
	if (i + h < n) { // 两个子序列一个长度小于h
		merge(arr,i, i + h - 1, n - 1);
	}
}

void mergeSort2(vector& arr,int n) {
	int h = 1;
	while (h < n) { // 两个子序列一个长度小于h
		mergePass(arr,h, n); // 一趟归并排序
		h = 2 * h;
	}
}
int main() {
	vector arr = { 6,4,2,3,9,1,4 };
	int n = arr.size();
	//mergeSort(arr, 0, n - 1);
	mergeSort2(arr,n);
	for (int i = 0; i < n; i++) {
		cout << " " << arr[i] << " " << endl;
	}
	system("pause");
	return 0;
}

---

本文参考书籍：数据结构----从概念到C++实现（第三版）王红梅、王慧、王新颖 编著