冒泡排序及其优化
一 概述
冒泡排序算法是一种典型的比较交换排序算法,在一个序列中进行数据的两两比较,如何和目标序列的规则相反就进行位置交换,如果相符,则两者的位置不变。故而冒泡排序是一个稳定的排序算法。
冒泡排序中所产生的有序子序列一定时全局有序的(不同与直接插入排序),也就是说,有序子序列中的所有元素的关键字一定小于或者大于无序子序列中所有元素的关键字,这样每趟排序都会将一个元素放置到其最终的位置上。
二 冒泡排序的实现过程
- 比较相邻的元素,如果第一个元素比第二个元素与目标队列元素的顺序规则相反,就进行交换。
- 对于每一对相邻元素进行同样的比较,从开始第一对到结尾的最后一对,那么最后的元素应该会是序列中最大或最小的数。
- 对序列中所有的元素重复以上的步骤,除最后一个元素除外;
- 重复以上几个步骤,直至排序完成。
![]()
三 冒泡排序性能
| 算法 | 最好时间 | 最坏时间 | 平均时间 | 额外空间 | 稳定性 |
|---|---|---|---|---|---|
| 冒泡 | O(n) | O(n^2) | O(n^2) | O(1) | 稳定 |
关于稳定性:因为在比较的过程中,当两个相同大小的元素相邻,只比较大或者小,所以相等的时候是不会交换位置的。而当两个相等元素离着比较远的时候,也只是会把他们交换到相邻的位置。他们的位置前后关系不会发生任何变化,所以算法是稳定的。
冒泡排序的空间效率:仅仅使用了常数个辅助单元,因而空间复杂度为O(1)。
冒泡排序的时间复杂度:当待排序的序列为有序序列时,仅仅只需要比较n-1次,移动次数为0,从而最好的情况下的时间复杂度为O(n);当初序列为逆序时,需要进行n-1趟排序,第i趟排序要进行n-i次关键字的比较,而且每次比较之后都必须移动元素3次来交换元素位置。
从而,冒泡排序的最坏情况下的时间复杂度为O(n^2),其平均时间复杂度也为O(n^2)。
稳定性:由于i>j时,且A[i] = A[j]时,不会发生交换,所以冒泡排序时一种稳定的排序算法。
四 冒泡排序常规版
下面详细分析一下常规版的冒泡排序,整个算法流程其实就是上面实例所分析的过程。可以看出,我们在进行每一次大循环的时候,还要进行一个小循环来遍历相邻元素并交换。所以我们的代码中首先要有两层循环。
外层循环:即主循环,需要辅助我们找到当前第 i 小的元素来让它归位。所以我们会一直遍历 n-2 次,这样可以保证前 n-1 个元素都在正确的位置上,那么最后一个也可以落在正确的位置上了。
内层循环:即副循环,需要辅助我们进行相邻元素之间的比较和换位,把大的或者小的浮到水面上。所以我们会一直遍历 n-1-i 次这样可以保证没有归位的尽量归位,而归位的就不用再比较了。
而上面的问题,出现的原因也来源于这两次无脑的循环,正是因为循环不顾一切的向下执行,所以会导致在一些特殊情况下得多余。例如 5,4,3,1,2 的情况下,常规版会进行四次循环,但实际上第一次就已经完成排序了。
/**
* 冒泡排序常规版
*/
public class BubbleSortNormal {
public static void main(String[] args) {
int[] list = {3,4,1,5,2};
int temp = 0; // 开辟一个临时空间, 存放交换的中间值
// 要遍历的次数
for (int i = 0; i < list.length-1; i++) {
System.out.format("第 %d 遍:\n", i+1);
//依次的比较相邻两个数的大小,遍历一次后,把数组中第i小的数放在第i个位置上
for (int j = 0; j < list.length-1-i; j++) {
// 比较相邻的元素,如果前面的数小于后面的数,就交换
if (list[j] < list[j+1]) {
temp = list[j+1];
list[j+1] = list[j];
list[j] = temp;
}
System.out.format("第 %d 遍的第%d 次交换:", i+1,j+1);
for(int count:list) {
System.out.print(count);
}
System.out.println("");
}
System.out.format("第 %d 遍最终结果:", i+1);
for(int count:list) {
System.out.print(count);
}
System.out.println("\n#########################");
}
}
}运行结果:
五 算法的第一次优化
经过了上述的讨论和编码,常规的冒泡排序已经被我们实现了。那么接下来我们要讨论的就是刚刚分析时候提出的问题。
首先针对第一个问题,当我们进行完第三遍的时候,实际上整个排序都已经完成了,但是常规版还是会继续排序。
可能在上面这个示例下,可能看不出来效果,但是当数组是,5,4,3,1,2 的时候的时候就非常明显了,实际上在第一次循环的时候整个数组就已经完成排序,但是常规版的算法仍然会继续后面的流程,这就是多余的了。
为了解决这个问题,我们可以设置一个标志位,用来表示当前第 i 趟是否有交换,如果有则要进行 i+1 趟,如果没有,则说明当前数组已经完成排序。实现代码如下:
/**
* 冒泡排序优化第一版
*/
public class BubbleSoerOpt1 {
public static void main(String[] args) {
int[] list = {5,4,3,1,2};
int temp = 0; // 开辟一个临时空间, 存放交换的中间值
// 要遍历的次数
for (int i = 0; i < list.length-1; i++) {
int flag = 1; //设置一个标志位
//依次的比较相邻两个数的大小,遍历一次后,把数组中第i小的数放在第i个位置上
for (int j = 0; j < list.length-1-i; j++) {
// 比较相邻的元素,如果前面的数小于后面的数,交换
if (list[j] < list[j+1]) {
temp = list[j+1];
list[j+1] = list[j];
list[j] = temp;
flag = 0; //发生交换,标志位置0
}
}
System.out.format("第 %d 遍最终结果:", i+1);
for(int count:list) {
System.out.print(count);
}
System.out.println("");
if (flag == 1) {//如果没有交换过元素,则已经有序
return;
}
}
}
}运行结果中可以看到优化效果非常明显,比正常情况下少了两次的循环:
这个时候我们就来讨论一下上面留下的一个小地方!没错就是最优时间复杂度为O(n)的问题,我们在进行了这一次算法优化之后,就可以做到了。
当给我们一个数列,5,4,3,2,1,让我们从大到小排序。没错,这是已经排好序的啊,也就是说因为标志位的存在,上面的循环只会进行一遍,flag没有变成1,整个算法就结束了,这也就是 O(n) 的来历了!
六 算法的第二次优化
除了上面这个问题,在冒泡排序中还有一个问题存在,就是第 i 趟排的第 i 小或者大的元素已经在第 i 位上了,甚至可能第 i-1 位也已经归位了,那么在内层循环的时候,有这种情况出现就会导致多余的比较出现。例如:6,4,7,5,1,3,2,当我们进行第一次排序的时候,结果为6,7,5,4,3,2,1,实际上后面有很多次交换比较都是多余的,因为没有产生交换操作。
我们用刚刚优化过一次的算法,跑一下这个数组。
/**
* 冒泡排序优化第一版
*/
public class BubbleSoerOpt1 {
public static void main(String[] args) {
int[] list = {6,4,7,5,1,3,2};
int len = list.length-1;
int temp = 0; // 开辟一个临时空间, 存放交换的中间值
// 要遍历的次数
for (int i = 0; i < list.length-1; i++) {
int flag = 1; //设置一个标志位
//依次的比较相邻两个数的大小,遍历一次后,把数组中第i小的数放在第i个位置上
for (int j = 0; j < len-i; j++) {
// 比较相邻的元素,如果前面的数小于后面的数,交换
if (list[j] < list[j+1]) {
temp = list[j+1];
list[j+1] = list[j];
list[j] = temp;
flag = 0; //发生交换,标志位置0
}
System.out.format("第 %d 遍第%d 趟结果:", i+1, j+1);
for(int count:list) {
System.out.print(count);
}
System.out.println("");
}
System.out.format("第 %d 遍最终结果:", i+1);
for(int count:list) {
System.out.print(count);
}
System.out.println("");
if (flag == 1) {//如果没有交换过元素,则已经有序
return;
}
}
}
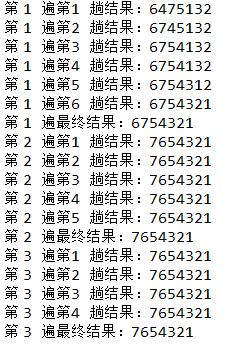
}运行结果中可以看出,第三趟的多次比较实际上可以没有,因为中间几个位置在第二趟就没有过交换。
针对上述的问题,我们可以想到,利用一个标志位,记录一下当前第 i 趟所交换的最后一个位置的下标,在进行第 i+1 趟的时候,只需要内循环到这个下标的位置就可以了,因为后面位置上的元素在上一趟中没有换位,这一次也不可能会换位置了。基于这个原因,我们可以进一步优化我们的代码。
/**
* 冒泡排序优化第二版
*/
public class BubbleSoerOpt2 {
public static void main(String[] args) {
int[] list = {6,4,7,5,1,3,2};
int len = list.length-1;
int temp = 0; // 开辟一个临时空间, 存放交换的中间值
int tempPostion = 0; // 记录最后一次交换的位置
// 要遍历的次数
for (int i = 0; i < list.length-1; i++) {
int flag = 1; //设置一个标志位
//依次的比较相邻两个数的大小,遍历一次后,把数组中第i小的数放在第i个位置上
for (int j = 0; j < len; j++) {
// 比较相邻的元素,如果前面的数小于后面的数,交换
if (list[j] < list[j+1]) {
temp = list[j+1];
list[j+1] = list[j];
list[j] = temp;
flag = 0; //发生交换,标志位置0
tempPostion = j; //记录交换的位置
}
System.out.format("第 %d 遍第%d 趟结果:", i+1, j+1);
for(int count:list) {
System.out.print(count);
}
System.out.println("");
}
len = tempPostion; //把最后一次交换的位置给len,来缩减内循环的次数
System.out.format("第 %d 遍最终结果:", i+1);
for(int count:list) {
System.out.print(count);
}
System.out.println("");
if (flag == 1) {//如果没有交换过元素,则已经有序
return;
}
}
}
}运行结果中,可以清楚的看到,部分内循环多余的比较已经被去掉了,算法得到了进一步的优化:
综上所述,冒泡排序是比较交换排序算法中的一种。