【读点论文】结构化剪枝

结构化剪枝

• 在一个神经网络模型中，通常包含卷积层、汇合层、全连接层、非线形层等基本结构，通过这些基本结构的堆叠，最终形成我们所常用的深度神经网络。

• 早在 1998 年，LeCun 等人使用少数几个基本结构组成 5 层的 LeNet-5 网络，并在 MNIST 数据集上得到了 98.9%的分类精度，但此时的深度神经网络还相对简单，并且只能用于简单的任务上；在 2012 年的 ImageNet 图像分类竞赛中，AlexNet将深度提高到了 8 层，并且达到了远超传统方法的结果；此后，VGG团队提出的 VGG-Net进一步加深了网络，使网络最高达到了 19 层。虽然增加网络的深度能够带来性能的提升，但也不能无限制的增加网络深度，随着网络的加深，梯度消失会愈发严重，并且模型会变得愈发难以训练。因此在 2016 年，He 等人提出 ResNet，在模型中加入残差结构，并一举将网络的深度提高到 152 层。至此，随着深度学习的研究逐步推进，神经网络可以变得更宽更深更复杂，与此同时带来更好的表示能力和性能表现。

• 模型压缩大致上可以分为四类：模型量化、模型剪枝、低秩近似和知识蒸馏。通常来说我们用 32 位浮点数来保存模型，模型量化主要考虑用更小位数来保存模型参数，通常使用的有 16 位浮点数和 8 位整数，其参数量和计算量都会相应地随着存储位数而成倍降低；更有甚者，将模型量化成二值网络，三元权重或者同或网络。经过简单量化之后的 MobileNetV1仅仅只有 4-5MB，能够轻松部署在各种移动平台上。

• 模型剪枝主要分为结构化剪枝和非结构化剪枝，非结构化剪枝去除不重要的神经元，相应地，被剪除的神经元和其他神经元之间的连接在计算时会被忽略。由于剪枝后的模型通常很稀疏，并且破坏了原有模型的结构，所以这类方法被称为非结构化剪枝。非结构化剪枝能极大降低模型的参数量和理论计算量，但是现有硬件架构的计算方式无法对其进行加速，所以在实际运行速度上得不到提升，需要设计特定的硬件才可能加速。与非结构化剪枝相对应的是结构化剪枝，结构化剪枝通常以滤波器或者整个网络层为基本单位进行剪枝。一个滤波器被剪枝，那么其前一个特征图和下一个特征图都会发生相应的变化，但是模型的结构却没有被破坏，仍然能够通过 GPU 或其他硬件来加速，因此这类方法被称之为结构化剪枝。

• 低秩近似将一个较大的卷积运算或者全连接运算替换成多个低维的运算。常用的低秩近似方法有 CP 分解法，Tucker 分解和奇异值分解。例如，一个 × 的全连接操作若能近似分解为 × 和 × （其中 ≪ , ）那么这一层全连接操作的计算量和参数量将被极大地缩减。

• 知识蒸馏（Knowledge Distillation）通过使用一个足够冗余的教师模型，来将其知识 “传授”给紧凑的学生模型。在训练时同时使用教师模型的软标签和真实标记的硬标签来共同训练学生模型，从而能够使学生模型达到接近教师模型的性能，也因此能够降低达到目标精度所需的计算量和模型大小。

• FLOPs（Floating-point operations）是浮点计算量的简称，通常使用 FLOPs 来表示模型的计算复杂度。将一个输入通道数为，输出通道数为的卷积层简化记为[, , ]，表示这个卷积层里有个 × × 的卷积单元，分别和输入特征进行卷积操作。这里我们将一次乘加(multiply and accumulate)算作两个浮点运算，所以对于输入为 × × 的特征，经过这一层卷积的浮点运算量为$FLOPs=2HWCin{k}^{2}Cout+HWCout$，其中表示偏置加法带来的计算量。参数量即为所含参数的数量，一个卷积层的参数量 $Params=K^{2}CinCout+Cout$ ，等号右边的两项分别表示卷积核和偏置的参数量。我们使用一个两层的卷积网络来展示滤波器剪枝的细节，为简化模型，我们均使用卷积核为 3、步长为 1 的普通卷积，并且不考虑卷积中的偏置操作。在我们的简化模型中，每层卷积的浮点计算量为18，参数量为9。

• 我们以这个简化的两层卷积网络为例来对剪枝过程进行分析。假定第一层卷积的输入和输出通道数分别为1和2，第二层卷积的输入和输出通道数分别为2和3。那么一个高度为、宽度为、通道数为1的输入特征1 ∈ ℝ××1 经过第一层卷积将得到中间特征2 ∈ ℝ××2，然后再经过第二层卷积操作得到输出特征3 ∈ℝ××3。这个双层卷积网络的参数量为92(1 + 3)，计算量为182(1 + 3)。我们对这个简单的双层卷积模型进行剪枝，将中间层的特征2由2个通道减少到2′个通道，那么相应地，第一个卷积层中产生2 − 2′个对应通道特征的卷积单元变得不再需要，所以新的卷积层可以表示为[2′ , 1, 3]；第二个卷积层中和相应通道特征进行卷积的参数也变得不再需要，所以新的卷积层可以表示为 [3, 2′ , 3]。因此，第一个卷积的输出通道数量和第二个卷积的输入通道数量都由2相应减少到2′，至此一个通道剪枝过程结束。

  • 

• 剪枝之后的双层卷积网络，其参数量变为92′ (1 + 3)，计算量变为182′ (1 +3)。当2′减小到2的一半时，这个简单双层网络的参数量和计算量都将减半。

• 相邻的两个卷积层紧紧联系在一起，第一个卷积层输出维度的变化将引起第二个卷积层的输入维度发生相应的变化。这样的卷积操作可以由第一个卷积层和第二个卷积层的组合，一直进行到倒数第二个卷积层和最后一个卷积层的组合。由于卷积层是用于视觉任务的神经网络的基础，所以对于几乎所有的网络结构，都可以使用滤波器级别剪枝（filter-level pruning）来减少参数量和计算量。大多数的剪枝算法也是基于滤波器级别剪枝来精简模型。滤波器级别剪枝的核心在于减少一个中间特征的数量，其前一个和后一个卷积层需要发生相应的变化。

• 残差结构的具体形 式 不唯一 ， 在 ResNet 中 的 残 差 结 构 由 三 层 卷 积 和 一 个 跨 层 连 接 构 成 ； 在MobileNetV2中，采用逐点卷积和逐层卷积来减少参数量和计算量，也有一个跨层连接。除此之外也有很多其他的形式，但是不管具体的构建形式如何，残差结构都可以表示为： $y=f(x)+x$.即残差结构的输出由两部分逐点相加得到：一部分是残差结构内最后一层卷积的输出，另一部分是残差结构的输入。由于需要进行逐点操作，所以这两部分的张量维度必须一致。当一个残差结构的输出直接作为下一个残差结构的输入时，等于说这两个残差结构的输出通道数是相等的，那么这两个残差结构紧密的联系在一起。通常会有其他操作夹在两个残差结构块之间（比如普通的卷积层，汇合层等），这样两个残差结构块之间的联系便被打破了。在残差结构块的联系没有被打破之前，多个残差结构块将紧密联系在一起，这些残差结构块的输出通道是对应起来的。我们将这样相互影响的多个残差结构块看成一个“阶段”（stage），常用的 ResNet-50 有四个阶段，这四个阶段分别有 3，4，6，3 个残差结构块。

  • 

• 滤波器级别的剪枝只能作用于残差结构块内部的卷积层，CURL中指出只进行滤波器级别的剪枝会导致模型形成一个沙漏状、两头宽中间窄的结构，这样的结构会影响的参数量和计算量。在这种情况下，阶段级别的剪枝能弥补滤波器级别剪枝的不足。

  • 

• 当一个阶段的输出特征发生变化时（一些特征被抛弃），其对应的每个残差结构的输入特征和输出特征都要发生相应的变化，所以整个阶段中，每个残差结构的第一个卷积层的输入通道数，以及最后一个卷积层的输出通道数都要发生相同的变化。由于这样的影响只限定在当前的阶段，不会影响之前和之后的阶段，因此我们称这个剪枝过程为阶段级别的剪枝（stage-level pruning）。阶段级别的剪枝加上滤波器级别的剪枝能够使网络的形状更均匀，而避免出现沙漏状的网络结构。此外，阶段级别的剪枝能够剪除更多的网络参数，这给网络进一步压缩提供了支持。

• 块级别的剪枝是直接丢弃某些残差结构块，由于残差结构的数学形式可以表达为 = () + ，丢弃残差结构后等于这一层变为 = 。以 ResNet 为例，其每个阶段的第一个残差结构通常会降低特征图的分辨率并提高特征图的通道数，所以除了每个阶段第一个残差结构块之外，其他的残差结构块都可以直接地被丢弃并且不影响整个网络的运行。这样的好处在于能降低网络的深度，从而获得相同大小的剪枝模型时，使用块级别剪枝的方法不至于过多减少每一层的通道数。加上块级别剪枝之后，一个 ResNet-50 模型能够很容易地剪枝得到计算量比例为 5%甚至更少的子模型。

• 剪枝算法的目的在于减少原模型的参数以及计算量，同时尽可能保证得到的子模型表达能力相比原模型来说损失较少。

剪枝的具体流程

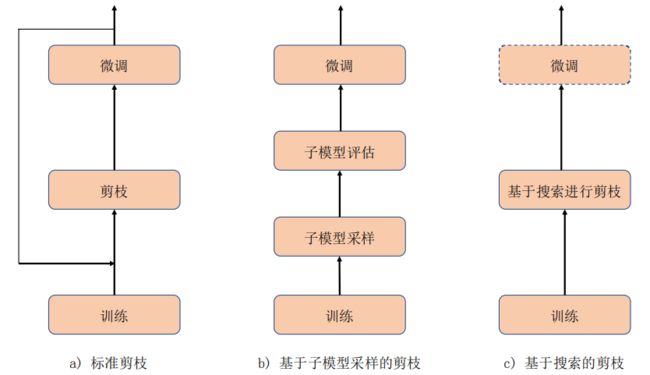
• 剪枝是减少模型参数量和计算量的经典方法。随着深度学习的兴起以及卷积神经网络在图像分类领域的大量应用，各种各样的剪枝方法也不断涌现出来。虽然剪枝的方法种类很多，但是其核心思想还是对神经网络的结构进行剪枝，目前剪枝算法的总体流程大同小异，可以归结为三类：标准剪枝、基于子模型采样的剪枝、以及基于搜索的剪枝.

  • 

  • 标准剪枝主要包含三个部分：训练、剪枝、以及微调。对于标准剪枝的流程详细说明如下：训练。在剪枝流程中，训练部分只需进行一次即可，训练的目的是为剪枝算法获取在特定任务上训练好的原始模型。

  • 剪枝。剪枝最重要的环节是对网络结构进行重要性评估，而这一重要性评估的环节也是各种剪枝算法最主要的区别之一。评估的模型结构主要包含滤波器、块等结构。对网络结构的重要性评估可以分为网络参数驱动的评估以及数据驱动的评估两类方法。

    • 基于网络参数驱动的方法利用模型本身的参数信息来衡量模型结构的重要性，如参数的1 正则化或者2 正则化，该类方法评估过程不依赖输入数据。

    • 基于数据驱动的方法通过利用训练数据来对网络结构的重要性作出评估，如通过统计滤波器输出结果经过激活层之后 0 值的个数来评价该滤波器的重要性。

  • 微调。微调是恢复被剪枝操作影响的模型表达能力的必要步骤。结构化模型剪枝会对原始模型结构进行调整，因此剪枝后的模型参数虽然保留了原始的模型参数，但是由于模型结构的改变，剪枝后模型的表达能力会受到一定程度的影响。微调过程通过将剪枝后的子模型在训练集进行微调训练，能够恢复子模型的表达能力。

  • 再剪枝。再剪枝过程将微调之后的子模型再送到剪枝模块中，再次进行模型结构评估和剪枝过程。通过再剪枝过程，使得每次剪枝都在性能更优的模型上面进行，不断阶段性的优化剪枝模型，直到模型能够满足剪枝目标需求。

• 标准剪枝流程是目前剪枝算法的主要流程，同时在标准剪枝的基础上，有些相关工作对标准剪枝过程进行改进,将剪枝过程集成到模型微调中，不再区分微调和剪枝两部分；提出一个新的可训练的网络层用于剪枝过程，该网络层生成二进制码，二进制码中的 0 值对应的网络结构将被剪掉。通过计算原始模型和去掉对应网络结构的子模型之间的 KL 散度来衡量每一个网络结构的重要性，这种计算方式使得网络结构评估不局限在局部特征或者参数中，而是利用全局特征，使得评估结果更为精确，因此其无需再剪枝过程便能达到很好的剪枝效果。

• 除标准剪枝之外，基于子模型采样的剪枝最近也表现出很好的剪枝效果。基于子模型采样的剪枝流程如图 b) 所示，得到训练好的模型之后，进行子模型采样过程。一次子模型采样过程为：

  • 1）对训练好的原模型中可修剪的网络结构按照剪枝目标进行采样，采样可以是随机的，也可以按照网络结构的重要性进行概率采样；

  • 2）对采样出的网络结构进行修剪，得到采样子模型。子模型采样过程通常进行次，得到个子模型（ ≥ 1）,之后对每一个子模型进行性能评估。子模型评估结束之后，选取最优的子模型进行微调以得倒最后的剪枝模型。

• 基于搜索的剪枝主要依靠强化学习或者神经网络结构搜索相关理论，其主要流程如图 c) 所示。给定剪枝目标之后，基于搜索的剪枝在网络结构中搜索较优的子结构，这个搜索过程往往伴随着网络参数的学习过程，因此一些基于搜索的剪枝算法在剪枝结束后无需再进行微调。

• 通常从三个方面评价神经网络剪枝算法的优劣：准确率及准确率变化、模型大小变化、以及网络前向时间变化。在实际实验中，这三种指标都需要统计，来综合体现剪枝算法的效果。

  • 准确率及准确率变化。在测试剪枝算法的实验结果时，需要在数据集的验证集上统计剪枝子模型的 Top-1 验证集准确率以及 Top-5 验证集准确率作为剪枝子网络的性能指标。同时，需要记录剪枝子模型准确率相对于原始模型的准确率变化（通常是负数），准确率变化大表明该子模型相比原模型准确率下降明显。

  • 模型大小变化。剪枝实验的一个重要目的是减少原始模型的参数量，因此需要统计剪枝子模型的模型参数量相比于原始模型的变化量。该模型参数变化量作为模型大小变化的指标，变化量越大表示模型大小压缩的越多。

  • 网络前向时间变化。对神经网络进行剪枝的最终目的在于保证子模型准确率的前提下，减少子模型的部署需求以及其运行时间，而运行时间仅靠模型大小、甚至 FLOPs 大小来衡量都是不准确的，因为有些模型参数量、FLOPs 虽然小，但是其结构不适应于硬件架构，所以其实际运行时间可能并未提升。模型前向时间变化可以由模型在硬件上的前向时间来体现，FLOPs 可供参考。

• 剪枝过程通过定义重要性指标来剪除相对不重要的参数。剪枝的指标往往是启发式的，根据评估指标时所利用的信息，基于重要性的模型剪枝算法评估准则可分为数据驱动和参数驱动两类。

参数驱动的评估准则

• 基于参数驱动的评估准则，其网络结构评估无需依赖输入数据，最常用的方式为1正则化和2正则化。由于其评估过程不需要输入数据，只依赖模型本身的参数，因此其对计算资源要求较少。但基于参数驱动的方法通常需要预先设定一个参数剪枝阈值来决定要修剪掉的网络结构，这个阈值通常会根据网络结构变化而变化，需要按照实际任务进行调整，给剪枝工作带来了一定的时间损耗。

数据驱动的评估准则

• 基于数据驱动的评估准则进行网络结构重要性评估时需要利用输入数据，通常在特征层面、梯度层面、网络输出结果等方面进行分析。

• APoZ为数据驱动的经典方法之一，其将滤波器经过激活层后输出的特征层当中数值为 0 所占百分比作为该滤波器重要性的评估依据，值为 0 所占百分比越多则该滤波器重要性越低。HRank发现单个滤波器生成的特征层的平均秩总是变化不大的，同时其证明了秩越低的特征层对精度的贡献越小，因此HRank 通过修剪掉这些生成低秩特征层的滤波器达到剪枝目的。通过实验发现特征层之间具有线性关系，因此利用子空间聚类的思想对滤波器产生的特征层进行聚类来消除滤波器的冗余，达到剪枝目的。

• ThiNet根据下一层的特征输出来修剪当前层的滤波器，其主要思想是通过重构下一层的输入特征，即用下一层的输入的子集代替原来的输入得到尽可能类似原来的输出，这样子集以外的输入就可以去掉，同时其对应的前一层的滤波器也就可以修剪掉。采用了类似的特征层重建思想，通过迭代算法进行逐层剪枝，将网络每一层的特征重建问题转换为 LASSO 回归和最小二乘法重建误差，通过特征重建过程来修剪掉对特征层重建贡献较小的滤波器。PFA将主成分分析（PCA）用于特征分析中，对于每一层滤波器输出的特征层，先将特征层进行池化输出为向量，而后对各个特征向量进行 PCA 分析，去掉信息含量少的特征层对应的滤波器来达到剪枝目的。

• 和基于参数驱动的评估准则相比，基于数据驱动的评估准则评估方式不限于网络本身的参数，虽然需要的计算资源和评估时间增加，但是其可利用的空间由于输入数据的参与而变得更多。同时，针对不同的场景输入数据能够使得评估结果符合该应用场景下的数据特点，避免基于参数驱动的评估方法只局限于网络本身参数的缺点。基于数据驱动的评估准则方法受剪枝领域欢迎的程度高于基于参数驱动的方法，近几年提出的评估准则多为数据驱动的方法。

基于搜索的剪枝方法

• 神经网络结构搜索（Neural Architecture Search）近些年来在模型结构设计上得到了广泛的关注和研究。在传统的模式下，研究者基于经验手工设计神经网络的结构，这不仅需要巨大的人力成本，同时对于一些普通的研究者来说也是一个困难的任务。提出使用基于强化学习的神经网络结构搜索来代替人工设计，但搜索过程需要耗费巨大的计算资源。

• DARTS的提出，基于梯度的搜索方法凭借其速度优势逐渐成为主流。此时，开始有研究者将结构化剪枝建模成一个基于原型网络的搜索过程，基于原型网络搜索得到的子模型就是剪枝后的小模型。

• AMC早在 2018 年就使用强化学习方法来搜索剪枝结构，在 AMC 中，将每一层的输入特征维度、卷积核大小、步长等信息编码成一个状态，使用 DDPG智能体来预测行动，使用分类错误和 FLOPs 作为奖赏。

• ABCPruner使用人工蜂群算法来寻找最优的剪枝结构。和常规的剪枝方法不同，ABCPruner 寻找每层的通道数量，而不是去选择相对重要的通道。具体来说，每层所对应的通道数量组成一个可行解，所有可行解构成目标种群，直接使用子模型在数据集上的表现作为其适应度，使用人工蜂群算法来进行搜索。在 ILSVRC-2012 数据集上，ABCPruner 能够在减少 62.87% FLOPs 和 60%参数量的同时，使 ResNet-152 的精度保持不变。

• MetaPruning使用元学习来自动进行通道剪枝。MetaPruning 首先训练一个元网络（meta network），然后使用演化过程来搜索表现好的剪枝模型。MetaPruning 为每层搜索通道的数量，而不是具体的每一个通道，能极大缩小搜索空间；在减少 ResNet-50 模型25% FLOPs 时，在 ILSVRC-2012 上只比原模型降低 0.4%的 Top-1 准确率。

• 无论是哪种剪枝算法，剪枝之后的模型都可以看作是原模型的一个子模型。这些子模型从原模型中继承部分参数，再辅以一定的微调训练，能达到和原模型相当，甚至超过原模型的分类结果，与此同时用到更少的参数量和计算量。

• 随着物联网的兴起和智能手机的发展，越来越多的移动设备搭载深度学习模型来提供更智能的服务。而这些移动设备的计算能力相对较低、存储空间相对不足，轻量级的模型变得愈发重要。结构化剪枝是一个重要并且有效的精简模型的方法，通常会和参数量化以及低秩近似等其他方法共同使用来最大化压缩模型。非结构化剪枝破坏了模型原有的结构，虽然参数量和理论计算量都极大地降低了，但实际运行速度却并不乐观。和非结构化剪枝不同的是，结构化剪枝算法能在通用平台上运行，并且由于保持了原模型的结构，能在剪枝的基础上进行低秩近似，这是非结构化剪枝所无法做到的。

• 然而结构化剪枝也存在一些问题，通常需要经过评估-选择-微调这三个步骤才能得到一个精简的模型，更有甚者会逐层进行选择和微调，获取一个精简模型需要花费极长的时间；此外，绝大多数的研究都集中在图像分类的研究上，在目标检测、语义分割等更难的视觉任务上，成果还相对欠缺。