Python计算机视觉——第四章 照相机模型与增强现实
文章目录
- 引言
- 4.1 针孔照相机模型
-
- 4.1.1 投影矩阵
- 4.1.2 三维点的投影
- 4.1.3 照相机矩阵的分解
- 4.1.4 计算照相机中心
- 4.2 照相机标定
-
- 4.2.1 相机参数标定实验
- 4.2.2 数据集
- 4.2.3 相机标定代码
- 4.2.4 实验结果
- 4.2.5 实验结果分析
- 4.3 以平面和标记物进行姿态估计
- 4.4 增强显示
-
- 4.4.1 照相机矩阵到OpenGL格式
- 4.4.2 图像中放置虚拟物体
- 4.4.3 综合集成
引言
为了处理三维图像和平面图像之间的映射,需要在映射中加入照相机产生图像的投影过程,我们将讨论如何确定照相机的参数,以及在增强现实(AR)等方面的具体应用。
4.1 针孔照相机模型
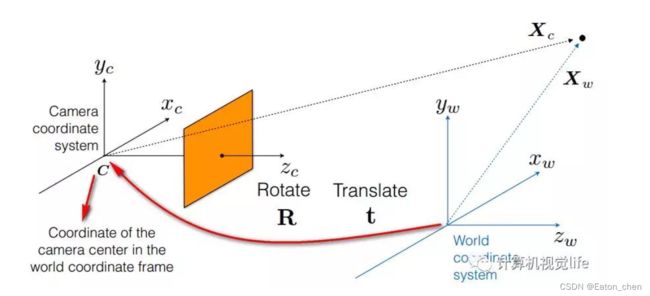
针孔照相机模型(射影照相机模型),在光线投影到图像平面之前,从照相机中心C经过(唯一一个点),模型如下图。
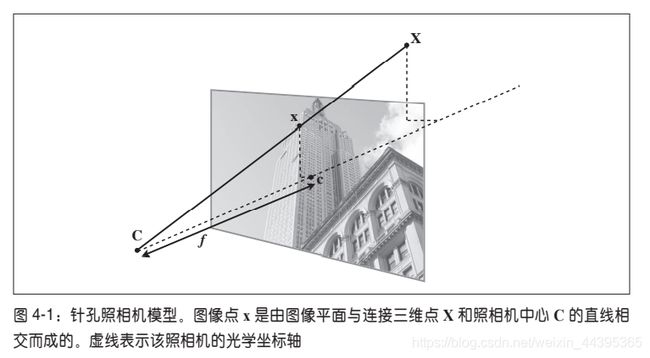
图像坐标轴和三维坐标系中的x轴、y轴对齐平行,光学坐标轴和z轴一致,在投影之前通过旋转和平移变换,在坐标系中加入三维点,会出现完整的投影变换。
针孔照相机中,三维点X投影为图像点x(齐次坐标表示),也就是把一个三维立体图形投影为二维图像,关系可由如下:
λ x = P X \lambda x=PX λx=PX P为(3,4)的投影矩阵,图像点的系数为逆深度,x=[X,Y,Z,W] (齐次坐标系),根据矩阵运算,行向量应为4。
4.1.1 投影矩阵
投影矩阵可分解为: P = K [ R ∣ t ] P=K[R|t] P=K[R∣t] R为旋转矩阵,t为三维平移向量,内标定矩阵K描述照相机的投影性质,大多数情况下,K可表示为: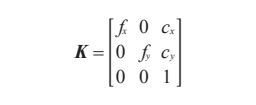
f是图像平面和C点的距离,即焦距,另一个参数是光心 c = [ c x , c y ] c=[c_x,c_y] c=[cx,cy],是z轴和图像平面的交点(在二维平面上),常接近于图像宽度和高度的一半,唯一未知的变量是焦距。
4.1.2 三维点的投影
根据三维点和图像点的关系,及三维投影的定义,可以写出投影的函数。
#导入线性代数部分
from scipy import linalg
class Camera(object):
""" Class for representing pin-hole cameras. """
def __init__(self,P):
""" Initialize P = K[R|t] camera model. """
self.P = P
# 标定矩阵
self.K = None # calibration matrix
self.R = None # rotation
self.t = None # translation
# 照相机中心
self.c = None # camera center
def project(self,X):
""" Project points in X (4*n array) and normalize coordinates. """
#定义和坐标归一化
# (3,n)
x = dot(self.P,X)
for i in range(3):
x[i] /= x[2]
return x
下载三维几何图像文件,来源于牛津大学的‘Model House’
import camera
# 载入点
points = loadtxt('house.p3d').T
points = vstack((points,ones(points.shape[1])))
# 设置照相机参数
# eye(3)是三阶单位矩阵
P = hstack((eye(3),array([[0],[0],[-10]])))
# 使用类Camera
cam = camera.Camera(P)
# 投影点
x = cam.project(points)
# 绘制投影
figure()
plot(x[0],x[1],'k.')
axis('off')
show()
制作围绕的三维向量,模拟旋转的投影
# 研究相机的移动如何影响投影的效果
# 获得三个随机数
r = 0.05*random.rand(3)
#创建围绕一个向量进行三维旋转的旋转矩阵
rot = camera.rotation_matrix(r)
# 旋转矩阵和投影
figure()
for t in range(20):
# 可见增减投影是在K的基础上点积
cam.P = dot(cam.P,rot)
x = cam.project(points)
plot(x[0],x[1],'k.')
show()
rotation_matrix:
def rotation_matrix(a):
""" Creates a 3D rotation matrix for rotation
around the axis of the vector a. """
R = eye(4)
R[:3,:3] = linalg.expm([[0,-a[2],a[1]],[a[2],0,-a[0]],[-a[1],a[0],0]])
return R
4.1.3 照相机矩阵的分解
如已给定照相机矩阵P,我们需要恢复内参数K以及照相机位置t和姿势R。这里使用RQ因子分解矩阵。
def factor(self):
""" Factorize the camera matrix into K,R,t as P = K[R|t]. """
# 分解前(3,3)
K,R = linalg.rq(self.P[:,:3])
# make K 对角为正值
T = diag(sign(diag(K)))
if linalg.det(T) < 0:
T[1,1] *= -1
self.K = dot(K,T)
# 令R为正定矩阵
self.R = dot(T,R) # T is its own inverse
self.t = dot(linalg.inv(self.K),self.P[:,3])
return self.K, self.R, self.t
运行如下代码,观察矩阵分解的结果。
import camera
K = array([[1000,0,500],[0,1000,300],[0,0,1]])
tmp = camera.rotation_matrix([0,0,1])[:3,:3]
Rt = hstack((tmp,array([[50],[40],[30]])))
cam = camera.Camera(dot(K,Rt))
print (K,Rt)
print (cam.factor())

(print k,Rt中)第一个矩阵是K,第二个矩阵是Rt(加了一行列向量[50,40,30] (t)),cam.factor第三个矩阵是t,R与K点积再分解。注意到两个t矩阵的第二个元素符号不相同。
4.1.4 计算照相机中心
公式: C = − R t t C=-R^ t t C=−Rtt 与内标定矩阵K无关。
下面代码计算照相机的中心。
def center(self):
""" Compute and return the camera center. """
# 如果存在的话
if self.c is not None:
return self.c
else:
# compute c by factoring
self.factor()
self.c = -dot(self.R.T,self.t)
return self.c
4.2 照相机标定
标定照相机是指计算该照相机的内参数,即计算矩阵K,K的计算唯一的未知参数是焦距。
步骤如下:
• 测量你选定矩形标定物体的边长 dX 和 dY;
• 将照相机和标定物体放置在平面上,使得照相机的背面和标定物体平行,同时物
体位于照相机图像视图的中心,你可能需要调整照相机或者物体来获得良好的对
齐效果;
• 测量标定物体到照相机的距离 dZ;
• 拍摄一副图像来检验该设置是否正确,即标定物体的边要和图像的行和列对齐;
• 使用像素数来测量标定物体图像的宽度和高度 dx 和 dy。
根据相似三角形原则
f x = d x d X d Z , f y = d y d X d Z f_x=\frac{dx}{dX}dZ, f_y=\frac{dy}{dX}dZ fx=dXdxdZ,fy=dXdydZ
可以使用交互式标注获得图像的4个点的像素。
from PIL import Image
from pylab import *
from numpy import *
im=array(Image.open('pic/calibration.JPG'))
imshow(im)
x=plt.ginput(4)
print('clicked points',x)
show()
因为版本问题,显示不了figure图像,所以以书上的数据为准。


第二张照片是手机里的图像,要用像素数来计算。dX=130,dY=185,dZ=460(mm),dx=722像素,dy=1040像素
计算得 f x = 2555 , f y = 2568 f_x=2555,f_y=2568 fx=2555,fy=2568,几乎是相同的。
返回K矩阵(得换算焦距)图像大小为(2592,2586)
def my_calibration(sz):
row,col = sz
fx = 2555*col/2592
fy = 2586*row/1936
K = diag([fx,fy,1])
K[0,2] = 0.5*col
K[1,2] = 0.5*row
return K
4.2.1 相机参数标定实验
我的摄像工具是iphone12,准备了5组照片。
相机的标定主要有两种: 传统的摄像头标定方法和摄像头自标定方法, 典型的有:(1)Tsai(传统的标定方法);(2)张正友(介于传统和自标定之间) 。1999年,微软研究院的张正友提出了基于移动平面模板的相机标定方法。 此方法是介于传统标定方法和自标定方法之间的一种方法, 传统标定方法虽然精度高设备有较高的要求, 其操作过程也比较繁琐, 自标定方法的精度不高, 张正友标定算法克服了这两者的缺点同时又兼备二者的优点, 因此对办公、 家庭的场合使用的桌面视觉系统 (DVS)很适合。张正友标定方法由于简单、效果好而得到广泛使用。
张正友标定方法的主要思想是:
利用一个棋盘格标定板,在得到一张标定板的图像之后,可以利用相应的图像检测算法得到每一个角点的像素坐标(u,v)。张正友标定法将世界坐标系固定于棋盘格上,则棋盘格上任一点的物理坐标 W=0,由于标定板的世界坐标系是人为事先定义好的,标定板上每一个格子的大小是已知的,我们可以计算得到每一个角点在世界坐标系下的物理坐标(U,V,W=0)。我们将利用这些信息:每一个角点的像素坐标(u,v)、每一个角点在世界坐标系下的物理坐标(U,V,W=0),来进行相机的标定,获得相机的内外参矩阵、畸变参数。
- 世界坐标系
世界坐标系(world coordinate)(xw,yw,zw),也称为测量坐标系,是一个三维直角坐标系,以其为基准可以描述相机和待测物体的空间位置。世界坐标系的位置可以根据实际情况自由确定。世界坐标系的最小单位为mm。
- 图像坐标系
图像坐标系(image coordinate)(x,y),是像平面上的二维直角坐标系。图像坐标系的原点为镜头光轴与像平面的交点(也称主点,principal point),它的x轴与相机坐标系的xc轴平行,它的y轴与相机坐标系的yc轴平行。图像坐标系的最小单位为mm。
- 相机坐标系
相机坐标系(camera coordinate)(xc,yc,zc),也是一个三维直角坐标系,原点位于镜头光心处,xc、yc轴分别与像面的两边平行,zc轴为镜头光轴,与像平面垂直。相机坐标系的最小单位为mm。
矩阵变换关系:
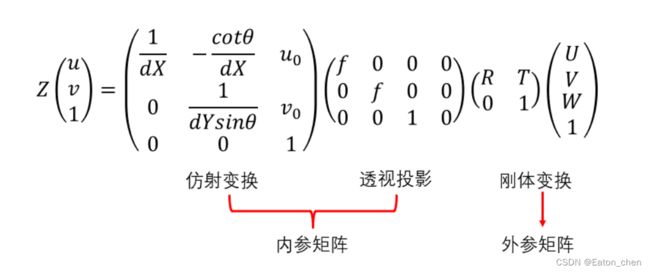
(U,V,W):世界坐标系下的物理坐标,(u,v):像素坐标系下的像素坐标;Z:尺度因子;f:像距;dX,dY表示X、Y方向上的一个像素在感光板上的物理长度;uo、vo表示像素在像素坐标系下的坐标, θ \theta θ表示横边和纵边之间的角度。
张正友标定法的标定步骤:
1、打印一张模板并贴在一个平面上;
2、从不同角度拍摄若干张模板图像;
3、检测出图像中的特征点;
4、求出摄像机的外参数(单应性矩阵)和内参数(最大似然估计) ;
5、求出畸变系数;
6、优化求精
4.2.2 数据集
我拍摄了五组图片,第一组将标定板置于地面,标定板不动,以地面作为参考系;第二组将手机置于支架上,保持手机不动,由人移动标定板;第三到第五组将标定板靠在柜子上,以近距离、中等距离、远距离拍摄。ps:每组分别拍摄了7张。
1.第一组
4.2.3 相机标定代码
import cv2
import numpy as np
import glob
# 设置寻找亚像素角点的参数,采用的停止准则是最大循环次数30和最大误差容限0.001
criteria = (cv2.TERM_CRITERIA_MAX_ITER | cv2.TERM_CRITERIA_EPS, 30, 0.001)
# 获取标定板角点的位置
#内角点个数,内角点是和其他格子连着的点
objp = np.zeros((8 * 11, 3), np.float32)
# 类似view() or permute()
objp[:, :2] = np.mgrid[0:11, 0:8].T.reshape(-1, 2) # 将世界坐标系建在标定板上,所有点的Z坐标全部为0,所以只需要赋值x和y
obj_points = [] # 存储3D点
img_points = [] # 存储2D点
i=0
# images = [str(i+1)+'.jpg' for i in range(10)]
# 图片不可以有中文符号
images = glob.glob('..\cam_img_test2\*.jpg')
print(len(images))
for fname in images:
img = cv2.imread(fname)
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
size = gray.shape[::-1]
# print(size)
ret, corners = cv2.findChessboardCorners(gray, (11, 8), None)
# print(corners)
if ret:
#存储3D点
obj_points.append(objp)
corners2 = cv2.cornerSubPix(gray, corners, (5, 5), (-1, -1), criteria) # 在原角点的基础上寻找亚像素角点
# print(corners2)
# 存储2D点
if [corners2]:
img_points.append(corners2)
else:
img_points.append(corners)
cv2.drawChessboardCorners(img, (11, 8), corners, ret) # 记住,OpenCV的绘制函数一般无返回值
i+=1;
cv2.imwrite('conimg'+str(i)+'.jpg', img)
cv2.waitKey(1500)
# print(len(img_points))
cv2.destroyAllWindows()
# 标定 去畸变
ret, mtx, dist, rvecs, tvecs = cv2.calibrateCamera(obj_points, img_points, size, None, None)
print("ret:布尔值:", ret)
print("内参数矩阵:\n", mtx) # 内参数矩阵
print("畸变系数:\n", dist) # 畸变系数 distortion cofficients = (k_1,k_2,p_1,p_2,k_3)
print("旋转向量:\n", rvecs) # 旋转向量 # 外参数
print("平移向量:\n", tvecs ) # 平移向量 # 外参数
4.2.4 实验结果
Test1:
ret:布尔值: 1.6438250920520316
内参数矩阵:
[[1.43737282e+03 0.00000000e+00 5.38106102e+02]
[0.00000000e+00 1.43495104e+03 9.33961260e+02]
[0.00000000e+00 0.00000000e+00 1.00000000e+00]]
畸变系数:
[[ 0.09077794 -0.87814912 0.01051167 0.01349766 2.67152693]]
旋转向量:
[array([[-6.81063313e-04],
[ 8.96223137e-02],
[ 1.57351637e+00]]), array([[-0.02161212],
[ 0.03204124],
[ 1.12192585]]), array([[-0.01487099],
[ 0.06364935],
[ 2.35275161]]), array([[ 0.2244866 ],
[-0.17701501],
[ 1.56072306]]), array([[ 0.26784391],
[-0.28890842],
[ 1.15095196]]), array([[ 0.08059618],
[-0.17853205],
[ 2.11661437]]), array([[-0.41645247],
[ 0.42061962],
[ 1.53137262]])]
平移向量:
[array([[ 3.30195595],
[-6.49710838],
[16.50790756]]), array([[ 0.991864 ],
[-6.16014088],
[22.01356395]]), array([[ 6.04643254],
[-1.34285118],
[23.83791922]]), array([[ 2.0307314 ],
[-10.97593417],
[ 24.88852363]]), array([[ -0.62344262],
[-11.44337978],
[ 26.55022287]]), array([[ 5.67530073],
[-1.3361333 ],
[22.79709381]]), array([[ 2.65478935],
[-9.52075854],
[25.64505021]])]
Test2:
ret:布尔值: 0.6570488418820846
内参数矩阵:
[[3.03737812e+03 0.00000000e+00 1.51797414e+03]
[0.00000000e+00 3.03428113e+03 2.01220092e+03]
[0.00000000e+00 0.00000000e+00 1.00000000e+00]]
畸变系数:
[[ 0.15014031 -0.48958994 -0.00208759 0.00119154 0.62628215]]
旋转向量:
[array([[-0.04301728],
[-0.00360016],
[-1.45323869]]), array([[ 0.610589 ],
[-0.58267148],
[-1.60163799]]), array([[ 0.01012138],
[ 0.66067419],
[-1.76500997]]), array([[-3.30792374e-04],
[-3.58161630e-02],
[-1.54720228e+00]]), array([[ 0.03560485],
[ 0.02197955],
[-1.54591276]]), array([[ 0.62062868],
[ 0.34778071],
[-0.74791852]]), array([[ 0.06633131],
[-0.75616275],
[-2.16681623]]), array([[-0.42271575],
[-0.25880969],
[-0.8581478 ]]), array([[-0.53014631],
[-0.50801259],
[-1.45604884]]), array([[-0.85101972],
[ 0.12263689],
[-1.49021001]])]
平移向量:
[array([[-5.65364531],
[-5.74866124],
[31.85055629]]), array([[-6.82561346],
[-4.56423562],
[31.35054521]]), array([[-2.98120939],
[-6.29948826],
[34.31197227]]), array([[-5.45915755],
[-8.05844685],
[46.94561408]]), array([[-4.75076409],
[-2.09322156],
[22.8709914 ]]), array([[-6.50207596],
[-7.66398594],
[29.7334409 ]]), array([[-1.29521813],
[-3.66722171],
[28.80349234]]), array([[-8.15161348],
[-8.31274042],
[31.12091844]]), array([[-5.66556367],
[-5.37770128],
[29.43778728]]), array([[-3.56814293],
[-4.26066421],
[33.15485447]])]
Test3:
ret:布尔值: 1.5428979002138428
内参数矩阵:
[[1.34539126e+03 0.00000000e+00 5.78628725e+02]
[0.00000000e+00 1.36470195e+03 9.17021501e+02]
[0.00000000e+00 0.00000000e+00 1.00000000e+00]]
畸变系数:
[[ 0.16312043 -1.13421847 0.03137427 0.01723009 2.50889906]]
旋转向量:
[array([[ 0.17432138],
[ 0.18105443],
[-1.53646967]]), array([[-0.36210563],
[ 1.00703995],
[-1.1792738 ]]), array([[-0.1652413 ],
[ 0.39926339],
[-1.50684377]]), array([[ 0.6114796 ],
[-0.21877223],
[-1.53021509]]), array([[ 0.47848585],
[ 0.35454455],
[-1.50403522]]), array([[ 0.65390554],
[ 0.57461005],
[-1.43236231]]), array([[ 1.19807423],
[-0.41270262],
[-1.5564332 ]])]
平移向量:
[array([[-4.36680237],
[ 5.16415121],
[20.49607147]]), array([[-2.94224732],
[ 3.11685785],
[23.15104023]]), array([[-4.94987684],
[ 4.97313464],
[21.0837629 ]]), array([[-6.28451325],
[ 2.06039689],
[23.70829341]]), array([[-6.00688925],
[ 2.55688617],
[21.93449142]]), array([[-5.47098619],
[ 3.8921101 ],
[22.74854593]]), array([[-3.73108949],
[ 4.0911408 ],
[19.32409611]])]
Test4:
ret:布尔值: 0.29303784789284903
内参数矩阵:
[[1.47194378e+03 0.00000000e+00 4.79241115e+02]
[0.00000000e+00 1.43556362e+03 9.45648630e+02]
[0.00000000e+00 0.00000000e+00 1.00000000e+00]]
畸变系数:
[[-2.19976781e-01 2.80946298e+00 -1.07772086e-02 2.41964511e-03
-1.14930267e+01]]
旋转向量:
[array([[ 0.22482687],
[ 0.28649499],
[-1.52985347]]), array([[ 0.0350748 ],
[ 0.55529716],
[-1.47254104]]), array([[-0.20929001],
[ 0.73499814],
[-1.42324539]]), array([[-0.38801345],
[ 0.90781023],
[-1.28958268]]), array([[-0.56926305],
[ 1.00004431],
[-1.20039276]]), array([[ 0.7848697 ],
[-0.16937472],
[-1.63528441]]), array([[ 0.90757476],
[-0.17541867],
[-1.65025789]])]
平移向量:
[array([[-4.56184776],
[-3.22330926],
[46.90161259]]), array([[-5.17538035],
[-4.38570201],
[52.20166407]]), array([[-3.52573594],
[-1.74126518],
[50.85637319]]), array([[-0.61291974],
[-2.33234916],
[52.40521705]]), array([[ 0.6578254 ],
[ 0.24683091],
[46.80446135]]), array([[-4.44366011],
[-1.44633046],
[38.72273229]]), array([[-2.16388241],
[-2.58070992],
[42.68990039]])]
Test5:
ret:布尔值: 0.13285023503151638
内参数矩阵:
[[1.49075623e+03 0.00000000e+00 3.92348361e+02]
[0.00000000e+00 1.44476933e+03 9.61865243e+02]
[0.00000000e+00 0.00000000e+00 1.00000000e+00]]
畸变系数:
[[-3.13394252e-02 2.04626478e+00 1.06784581e-02 -1.18605038e-02
-1.08944882e+01]]
旋转向量:
[array([[ 0.17670139],
[ 0.35432323],
[-1.52590984]]), array([[-0.00757966],
[ 0.65440077],
[-1.43661738]]), array([[-0.23860396],
[ 0.80640659],
[-1.3613819 ]]), array([[-0.48848273],
[ 0.94010245],
[-1.29010955]]), array([[ 0.62981803],
[-0.10788316],
[-1.6135827 ]]), array([[ 0.84400613],
[-0.30787682],
[-1.70533168]]), array([[ 0.93434599],
[-0.44528773],
[-1.67340744]])]
平移向量:
[array([[-4.01894466e-02],
[-1.54921218e+01],
[ 9.30059410e+01]]), array([[ 1.57037205],
[-15.71216485],
[ 91.5386359 ]]), array([[ 2.69532873],
[-9.37652601],
[86.94495178]]), array([[ 5.34046431],
[-1.52268073],
[76.99177274]]), array([[ 2.33578307],
[-5.55852066],
[66.95081315]]), array([[ 1.92209612],
[-4.09620077],
[61.99171096]]), array([[ 6.27697843],
[ 0.84890036],
[59.23783514]])]
4.2.5 实验结果分析
第二组的结果误差较大,手机不动、移动标定板获得的结果并不可靠;第一组和三、四、五组参照系不同,得到的结果有所差异;三四五组参照系不变,但拍摄距离的远近也会影响相机参数的变化。总的来说,第一组的实验结果是最可信的,因为将标定板置于地面,z轴的值就接近为零。
4.3 以平面和标记物进行姿态估计
如果图像中包含平面状的标记物,并且对照相机进行了标定,那么可以计算出照相机的姿态(旋转和平移)。
先提取SIFT特征,再使用RANSAC算法稳健地估计单应性算法,是第二章和第三章的知识点,基础要打扎实。
import homography
import camera
import sift
# 计算特征
sift.process_image('pic/book_frontal.JPG','im0.sift')
l0,d0 = sift.read_features_from_file('im0.sift')
sift.process_image('pic/book_perspective.JPG','im1.sift')
l1,d1 = sift.read_features_from_file('im1.sift')
# 匹配特征,并计算单应性矩阵
matches = sift.match_twosided(d0,d1)
ndx = matches.nonzero()[0]
fp = homography.make_homog(l0[ndx,:2].T)
ndx2 = [int(matches[i]) for i in ndx]
tp = homography.make_homog(l1[ndx2,:2].T)
model = homography.RansacModel()
H,ransac_data = homography.H_from_ransac(fp,tp,model)
单应性矩阵将标记物(书本)上的点映射到另一图像中的对应点,下面我们定义相应的三维坐标系,使标记物在X-Y平面上(z=0)。
制作立方体:
def cube_points(c,wid):
p = []
# 底部
p.append([c[0]-wid,c[1]-wid,c[2]-wid])
p.append([c[0]-wid,c[1]+wid,c[2]-wid])
p.append([c[0]+wid,c[1]+wid,c[2]-wid])
p.append([c[0]+wid,c[1]-wid,c[2]-wid])
p.append([c[0]-wid,c[1]-wid,c[2]-wid]) # 为了绘制闭合图像,和第一个相同
# 顶部
p.append([c[0]-wid,c[1]-wid,c[2]+wid])
p.append([c[0]-wid,c[1]+wid,c[2]+wid])
p.append([c[0]+wid,c[1]+wid,c[2]+wid])
p.append([c[0]+wid,c[1]-wid,c[2]+wid])
p.append([c[0]-wid,c[1]-wid,c[2]+wid]) # 为了绘制闭合图像,和第一个相同
# 竖直边
p.append([c[0]-wid,c[1]-wid,c[2]+wid])
p.append([c[0]-wid,c[1]+wid,c[2]+wid])
p.append([c[0]-wid,c[1]+wid,c[2]-wid])
p.append([c[0]+wid,c[1]+wid,c[2]-wid])
p.append([c[0]+wid,c[1]+wid,c[2]+wid])
p.append([c[0]+wid,c[1]-wid,c[2]+wid])
p.append([c[0]+wid,c[1]-wid,c[2]-wid])
return array(p).T
这里我们使用图像的分辨率为 747×1000,第一个产生的标定矩阵就是在该图像分辨率大小下的标定矩阵。下面,我们在原点附近创建立方体上的点。cube_points()函数产生的前五个点对应于立方体底部的点,在这个例子中对应于位于标记物上
Z=0 平面内的点。第一幅图像是书本的主视图,我们将其作为这个例子中的模板图像。因为场景坐标的尺度是任意的,所以我们使用下面的矩阵来创建第一个照相机:
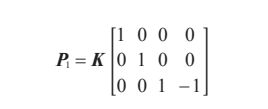
其中,图像的坐标轴和照相机是对齐的,并且放置在标记物的正上方。将前 5 个三维点投影到图像上。有了估计出的单应性矩阵,我们可以将其变换到第二幅图像上。绘制出变换后的图像,并在同样的标记物位置绘制出这些点(如图 4-4 右上所示)。
现在,结合 P1 和 H 构建第二幅图像的照相机矩阵: P 2 = H P 1 P_2=HP_1 P2=HP1 该矩阵将标记平面 Z=0 上的点变换到正确的位置。也就是说,P2 矩阵的前两列和第四列是正确的。由于我们知道前 3×3 矩阵块应该为 KR,并且 R 是旋转矩阵,所以我们可以将 P2 乘以标定矩阵的逆,然后将第三列替换为前两列的交叉乘积,以此来恢复第三列。作为合理性验证,我们可以使用新矩阵投影标记平面的一个点,然后检查投影后的点是否与使用第一个照相机和单应性矩阵变换后的点相同。你会发现,控制台上得到了相同的输出结果。
# 计算照相机标定矩阵
K = my_calibration((747,1000))
# 位于边长为 0.2,z=0 平面上的三维点
box = cube_points([0,0,0.1],0.1)
# 投影第一幅图像上底部的正方形
cam1 = camera.Camera( hstack((K,dot(K,array([[0],[0],[-1]])) )) )
# 底部正方形上的点
box_cam1 = cam1.project(homography.make_homog(box[:,:5]))
# 使用 H 将点变换到第二幅图像中
box_trans = homography.normalize(dot(H,box_cam1))
# 从 cam1 和 H 中计算第二个照相机矩阵
cam2 = camera.Camera(dot(H,cam1.P))
A = dot(linalg.inv(K),cam2.P[:,:3])
A = array([A[:,0],A[:,1],cross(A[:,0],A[:,1])]).T
cam2.P[:,:3] = dot(K,A)
# 使用第二个照相机矩阵投影
box_cam2 = cam2.project(homography.make_homog(box))
# 测试:将点投影在 z=0 上,应该能够得到相同的点
point = array([1,1,0,1]).T
rcParams['font.sans-serif'] = ['SimHei']
im0 = array(Image.open('pic/book_frontal.JPG'))
im1 = array(Image.open('pic/book_perspective.JPG'))
# 底部正方形的二维投影
figure()
imshow(im0)
axis('off')
plot(box_cam1[0,:],box_cam1[1,:],linewidth=3)
title('二维投影')
# 使用 H 对二维投影进行变换
figure()
imshow(im1)
axis('off')
plot(box_trans[0,:],box_trans[1,:],linewidth=3)
title('变换二维投影')
# 三维立方体
figure()
imshow(im1)
plot(box_cam2[0,:],box_cam2[1,:],linewidth=3)
axis('off')
title('三维立方体')
使用pickle板块保存照相机矩阵数据。
import pickle
with open('ar_camera.pkl','wb') as f:
pickle.dump(K,f)
pickle.dump(dot(linalg.inv(K),cam2.P),f)
4.4 增强显示
增强现实(Augmented Reality,AR)是将物体和相应信息放置在图像数据上的一系列操作的总称。最经典的例子是放置一个三维计算机图形学模型,使其看起来属于该场景;如果在视频中,该模型会随着照相机的运动很自然地移动。
4.4.1 照相机矩阵到OpenGL格式
已 pip install pygame(游戏开发包)和pyopengl(图形编程的python绑定窗口),照相机与场景的变换分成了两个矩阵GL_PROJECTION 矩阵和 GL_MODELVIEW 矩阵。GL_PROJECTION 矩阵处理图像成像的性质,等价于我们的内标定矩阵 K。GL_MODELVIEW 矩阵处理物体和照相机之间的三维变换关系,对应于我们照相机矩阵中的 R 和 t 部分。
投影矩阵:
from numpy import *
def set_projection_from_camera(K):
glMatrixMode(GL_PROJECTION)
glLoadIdentity()
# 焦距
fx = K[0,0]
fy = K[1,1]
# 照相机看到的范围 0-180度
fovy = 2*arctan(0.5*height/fy)*180/pi
# 纵横比
aspect = (width*fy)/(height*fx)
# 定义近的和远的剪裁平面
near = 0.1
far = 100.0
#设置透视
gluPerspective(fovy,aspect,near,far)
glViewport(0,0,width,height)
模拟视图矩阵:4*4 (Rt)

R为旋转矩阵,列向量为3个坐标轴的方向,t使平移向量,下面函数实现移除标定矩阵后的照相机矩阵(dot(P,1/k),并创建模拟视图,R的最佳逼近矩阵由SVD分解后的左右奇异矩阵点积。
def set_modelview_from_camera(Rt):
glMatrixMode(GL_MODELVIEW)
glLoadIdentity()
# 围绕x 轴将茶壶旋转 90 度,使z 轴向上
Rx = array([[1,0,0],[0,0,-1],[0,1,0]])
R = Rt[:,:3]
U,S,V = linalg.svd(R)
R = dot(U,V)
R[0,:] = -R[0,:] # 改变x轴的符号
# 获得平移量
t = Rt[:,3]
# 获得 4×4 的模拟视图矩阵
M = eye(4)
# 改变方向
M[:3,:3] = dot(R,Rx)
M[:3,3] = t
# 转置并压平以获取列序数值
M = M.T
m = M.flatten()
# 将模拟视图矩阵替换为新的矩阵
glLoadMatrixf(m)
4.4.2 图像中放置虚拟物体
首先使用 PyGame 中的一些函数来载入一幅图像,将其序列化为能够在PyOpenGL 中使用的原始字符串表示。然后,重置模拟视图,清除颜色和深度缓存。接下来,绑定这个纹理,使其能够在四边形和指定插值中使用它。四边形是在每一维分别为 -1 和 1 的点上定义的。
from OpenGL.GL import *
from OpenGL.GLU import *
from OpenGL.GLUT import *
def draw_background(imname):
# 载入背景图像(应该是 .bmp 格式),转换为 OpenGL 纹理
bg_image = pygame.image.load(imname).convert()
bg_data = pygame.image.tostring(bg_image,"RGBX",1)
glMatrixMode(GL_MODELVIEW)
glLoadIdentity()
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT)
# 绑定纹理
glEnable(GL_TEXTURE_2D)
glBindTexture(GL_TEXTURE_2D,glGenTextures(1))
glTexImage2D(GL_TEXTURE_2D,0,GL_RGBA,width,height,0,GL_RGBA,GL_UNSIGNED_BYTE,bg_data)
glTexParameterf(GL_TEXTURE_2D,GL_TEXTURE_MAG_fiLTER,GL_NEAREST)
glTexParameterf(GL_TEXTURE_2D,GL_TEXTURE_MIN_fiLTER,GL_NEAREST)
# 创建四方形填充整个窗口
glBegin(GL_QUADS)
glTexCoord2f(0.0,0.0); glVertex3f(-1.0,-1.0,-1.0)
glTexCoord2f(1.0,0.0); glVertex3f( 1.0,-1.0,-1.0)
glTexCoord2f(1.0,1.0); glVertex3f( 1.0, 1.0,-1.0)
glTexCoord2f(0.0,1.0); glVertex3f(-1.0, 1.0,-1.0)
glEnd()
# 清除纹理
glDeleteTextures(1)
茶壶:
from OpenGL.GL import *
from OpenGL.GLU import *
from OpenGL.GLUT import *
def drawFunc():
glClear(GL_COLOR_BUFFER_BIT)
# glRotatef(1, 0, 1, 0)
glutWireTeapot(0.5)
glFlush()
glutInit()
glutInitDisplayMode(GLUT_SINGLE | GLUT_RGBA)
glutInitWindowSize(400, 400)
glutCreateWindow(b"First")
glutDisplayFunc(drawFunc)
# glutIdleFunc(drawFunc)
glutMainLoop()
4.4.3 综合集成
将照相机模型和增强现实结合起来,且引入pickle板块,代码集成度很高。
from OpenGL.GL import *
from OpenGL.GLU import *
from OpenGL.GLUT import *
import pygame, pygame.image
from pygame.locals import *
import pickle
width,height = 1000,747
def setup():
pygame.init()
pygame.display.set_mode((width,height),OPENGL | DOUBLEBUF)
pygame.display.set_caption('OpenGL AR demo')
# 载入照相机数据
with open('ar_camera.pkl','rb') as f:
K = pickle.load(f)
Rt = pickle.load(f)
setup()
draw_background('book_perspective.bmp')
set_projection_from_camera(K)
set_modelview_from_camera(Rt)
drawFunc()
while True:
event = pygame.event.poll()
if event.type in (QUIT,KEYDOWN):
break
pygame.display.flip()