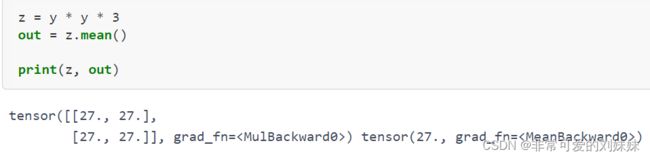
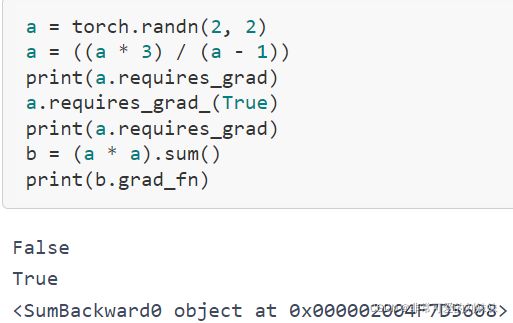
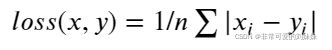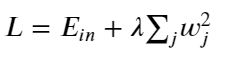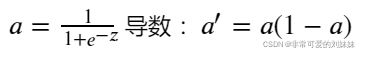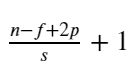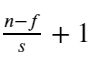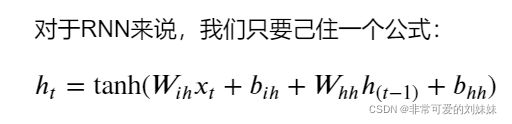pytorch学习（一）

1.torch

Torch是一个与Numpy类似的张量（Tensor）操作库，与Numpy不同的是Torch对GPU支持的很好，Lua是Torch的上层包装。

PyTorch和Torch使用包含所有相同性能的C库：TH, THC, THNN, THCUNN，并且它们将继续共享这些库。

这样的回答就很明确了，其实PyTorch和Torch都使用的是相同的底层，只是使用了不同的上层包装语言。

注：LUA虽然快，但是太小众了，所以才会有PyTorch的出现。

PyTorch是一个基于Torch的Python开源机器学习库，用于自然语言处理等应用程序。 它主要由Facebook的人工智能研究小组开发。Uber的"Pyro"也是使用的这个库。

PyTorch是一个Python包，提供两个高级功能：

• 具有强大的GPU加速的张量计算（如NumPy）
• 包含自动求导系统的的深度神经网络

2.PyTorch 深度学习:60分钟快速入门 （官方)

torch — PyTorch 1.11.0 documentation

pytorch api

2.1张量

1.from __future__ import print_function

该句语句是python2的概念，那么python3对于python2就是future了，也就是说，在python2的环境下，超前使用python3的print函数。

 所以以后看到这个句子的时候，不用害怕，只是把下一个新版本的特性导入到当前版本！

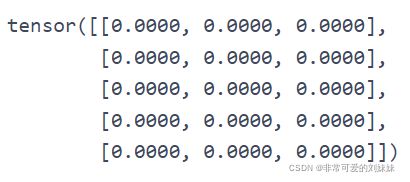
2.x = torch.empty(5, 3)  创建一个 5x3 矩阵, 但是未初始化:

 根据现有的张量创建张量。 这些方法将重用输入张量的属性，例如， dtype，除非设置新的值进行覆盖

x = x.new_ones(5, 3, dtype=torch.double) # new_* 方法来创建对象

print(x)

x = torch.randn_like(x, dtype=torch.float) # 覆盖 dtype!

print(x)

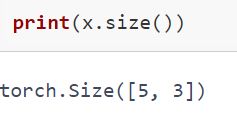
3. 使用size方法与Numpy的shape属性返回的相同，张量也支持shape属性

4.在python中，tuple元组这种数据结构同列表类似，都可以描述一组数据的集合，它们都是容器，是一系列组合的对象，不同的地方在于，元组里的元素是不能更改的，它们之间的差异性我们用一个例子来说明一下：

列表：

>>>find_files("*.txt")

["file1.txt","file2.txt","file3.txt","file4.txt"]

元组：

>>> student=(1,"tom","2008-05-06",10,135.7)

>>> print(student[1]) #输出 tom

从上面的比较例子可以看出，列表一般用于不确定个数的数据的集合中，例如上面，并不知道能找到多少个txt文件，所以用列表来表示，而元组一般用于描述一个东西的特性，例如上面的例子，描述了一个学生的学号、姓名、出生年月、年龄和身高，下面我们具体来学习元组这种数据类型；

5.加法运算

法一：y = torch.rand(5, 3)         

          print(x + y)

法二：print(torch.add(x, y))

法三：提供输出tensor作为参数

           result = torch.empty(5, 3)

           torch.add(x, y, out=result)

           print(result)

法四：y.add_(x)

           print(y)

任何 以``_`` 结尾的操作都会用结果替换原变量. 例如: ``x.copy_(y)``, ``x.t_()``, 都会改变 ``x``.

6.torch.view: 可以改变张量的维度和大小，与Numpy的reshape类似

x = torch.randn(4, 4)

y = x.view(16)#变一维数组

z = x.view(-1, 8) # size -1 从其他维度推断，这里变为8列（8,-1)变为8行

print(x.size(), y.size(), z.size())

torch.Size([4, 4]) torch.Size([16]) torch.Size([2, 8])

7.如果你有只有一个元素的张量，使用.item()来得到Python数据类型的数值

 8.Torch Tensor和NumPy数组转换

Torch Tensor与NumPy数组共享底层内存地址，修改一个会导致另一个的变化。

（1）将一个Torch Tensor转换为NumPy数组

b = a.numpy()

print(b)

[1. 1. 1. 1. 1.]

a.add_(1)

print(a) print(b)

 （2）NumPy Array 转化成 Torch Tensor，使用from_numpy自动转化

b = torch.from_numpy(a)

np.add(a, 1, out=a)

print(a) print(b)

9.所有的 Tensor 类型默认都是基于CPU， CharTensor 类型不支持到 NumPy 的转换. CUDA 张量

使用.to 方法 可以将Tensor移动到任何设备中

# is_available 函数判断是否有cuda可以使用
# ``torch.device``将张量移动到指定的设备中
if torch.cuda.is_available():
    device = torch.device("cuda")          # a CUDA 设备对象
    y = torch.ones_like(x, device=device)  # 直接从GPU创建张量
    x = x.to(device)                       # 或者直接使用``.to("cuda")``将张量移动到cuda中
    z = x + y
    print(z)
    print(z.to("cpu", torch.double))       # ``.to`` 也会对变量的类型做更改

tensor([0.7632], device='cuda:0')
tensor([0.7632], dtype=torch.float64)

2.2Autograd: 自动求导机制

PyTorch 中所有神经网络的核心是 autograd 包。torch.Tensor是这个包的核心类。

如果设置 .requires_grad 为 True，那么将会追踪所有对于该张量的操作。 当完成计算后通过调用 .backward()，自动计算所有的梯度， 这个张量的所有梯度将会自动积累到 .grad 属性。

要阻止张量跟踪历史记录，可以调用.detach()方法将其与计算历史记录分离，并禁止跟踪它将来的计算记录。

为了防止跟踪历史记录（和使用内存），可以将代码块包装在with torch.no_grad()：中。 在评估模型时特别有用，因为模型可能具有requires_grad = True的可训练参数，但是我们不需要梯度计算。

在自动梯度计算中还有另外一个重要的类Function.

Tensor 和 Function互相连接并生成一个非循环图，它表示和存储了完整的计算历史。 每个张量都有一个.grad_fn属性，这个属性引用了一个创建了Tensor的Function（除非这个张量是用户手动创建的，即，这个张量的 grad_fn 是 None）。

如果需要计算导数，你可以在Tensor上调用.backward()。 如果Tensor是一个标量（即它包含一个元素数据）则不需要为backward()指定任何参数， 但是如果它有更多的元素，你需要指定一个gradient 参数来匹配张量的形状。

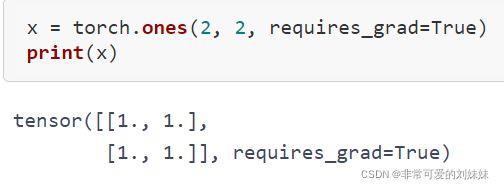
1.创建一个张量并设置 requires_grad=True 用来追踪他的计算历史

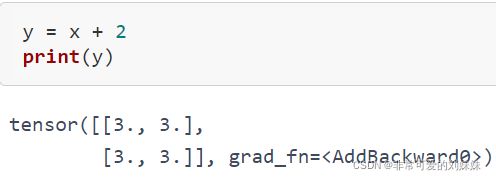
对张量进行操作:

结果y已经被计算出来了，所以，grad_fn已经被自动生成了。

 

 

 .requires_grad_( ... ) 可以改变现有张量的 requires_grad属性。 如果没有指定的话，默认输入的flag是 False。

2.梯度

反向传播 因为 out是一个标量（scalar），out.backward() 等于out.backward(torch.tensor(1))。

 

 一般来说，torch.autograd就是用来计算vector-Jacobian product的工具。

来看一个vector-Jacobian product的例子

 在这个情形中，y不再是个标量。torch.autograd无法直接计算出完整的雅可比行列，但是如果我们只想要vector-Jacobian product，只需将向量作为参数传入backward：

..........................

2.3神经网络

神经网络的典型训练过程如下：

1. 定义包含一些可学习的参数(或者叫权重)神经网络模型；
2. 在数据集上迭代；
3. 通过神经网络处理输入；
4. 计算损失(输出结果和正确值的差值大小)；
5. 将梯度反向传播回网络的参数；
6. 更新网络的参数，主要使用如下简单的更新原则： weight = weight - learning_rate * gradient

在模型中必须要定义 forward 函数，backward 函数（用来计算梯度）会被autograd自动创建。 可以在 forward 函数中使用任何针对 Tensor 的操作。

3.基础

torch.nn是专门为神经网络设计的模块化接口。nn构建于 Autograd之上，可用来定义和运行神经网络。

nn.functional，这个包中包含了神经网络中使用的一些常用函数，这些函数的特点是，不具有可学习的参数(如ReLU，pool，DropOut等)，这些函数可以放在构造函数中，也可以不放，但是这里建议不放。

3.1定义一个网络

PyTorch中已经为我们准备好了现成的网络模型，只要继承nn.Module，并实现它的forward方法，PyTorch会根据autograd，自动实现backward函数，在forward函数中可使用任何tensor支持的函数，还可以使用if、for循环、print、log等Python语法，写法和标准的Python写法一致。

class Net(nn.Module):
    def __init__(self):
        # nn.Module子类的函数必须在构造函数中执行父类的构造函数
        super(Net, self).__init__()

       # 卷积层 '1'表示输入图片为单通道， '6'表示输出通道数，'3'表示卷积核为3*3
        self.conv1 = nn.Conv2d(1, 6, 3)

       #线性层，输入1350个特征，输出10个特征
        self.fc1   = nn.Linear(1350, 10)  #这里的1350是如何计算的呢？这就要看后面的forward函数

         #正向传播

def forward(self, x): 
        print(x.size()) # 结果：[1, 1, 32, 32]
        # 卷积 -> 激活 -> 池化 
        x = self.conv1(x) #根据卷积的尺寸计算公式，计算结果是30，具体计算公式后面第二章第四节 卷积神经网络 有详细介绍。
        x = F.relu(x)
        print(x.size()) # 结果：[1, 6, 30, 30]
        x = F.max_pool2d(x, (2, 2)) #我们使用池化层，计算结果是15
        x = F.relu(x)
        print(x.size()) # 结果：[1, 6, 15, 15]
        # reshape，‘-1’表示自适应
        #这里做的就是压扁的操作 就是把后面的[1, 6, 15, 15]压扁，变为 [1, 1350]
        x = x.view(x.size()[0], -1) 
        print(x.size()) # 这里就是fc1层的的输入1350 
        x = self.fc1(x)        
        return x

net = Net()
print(net)

网络的可学习参数通过net.parameters()返回

for parameters in net.parameters():
    print(parameters)

net.named_parameters可同时返回可学习的参数及名称。

for name,parameters in net.named_parameters():
    print(name,':',parameters.size())

forward函数的输入和输出都是Tensor

input = torch.randn(1, 1, 32, 32) # 这里的对应前面fforward的输入是32
out = net(input)
out.size()

 input.size()

 在反向传播前，先要将所有参数的梯度清零

net.zero_grad() 
out.backward(torch.ones(1,10)) # 反向传播的实现是PyTorch自动实现的，我们只要调用这个函数即可

3.2损失函数

y = torch.arange(0,10).view(1,10).float()
criterion = nn.MSELoss()
loss = criterion(out, y)
#loss是个scalar，我们可以直接用item获取到他的python类型的数值
print(loss.item()) 

3.3优化器

在反向传播计算完所有参数的梯度后，还需要使用优化方法来更新网络的权重和参数，例如随机梯度下降法(SGD)的更新策略如下：

weight = weight - learning_rate * gradient

在torch.optim中实现大多数的优化方法，例如RMSProp、Adam、SGD等，下面我们使用SGD做个简单的样例

out = net(input) # 这里调用的时候会打印出我们在forword函数中打印的x的大小
criterion = nn.MSELoss()
loss = criterion(out, y)
#新建一个优化器，SGD只需要要调整的参数和学习率
optimizer = torch.optim.SGD(net.parameters(), lr = 0.01)
# 先梯度清零(与net.zero_grad()效果一样)
optimizer.zero_grad() 
loss.backward()

#更新参数
optimizer.step()

4.数据的加载和预处理

PyTorch通过torch.utils.data对一般常用的数据加载进行了封装，可以很容易地实现多线程数据预读和批量加载。 并且torchvision已经预先实现了常用图像数据集，包括前面使用过的CIFAR-10，ImageNet、COCO、MNIST、LSUN等数据集，可通过torchvision.datasets方便的调用

Dataset

Dataset是一个抽象类，为了能够方便的读取，需要将要使用的数据包装为Dataset类。 自定义的Dataset需要继承它并且实现两个成员方法：

1. __getitem__() 该方法定义用索引(0 到 len(self))获取一条数据或一个样本
2. __len__() 该方法返回数据集的总长度

#引用
from torch.utils.data import Dataset
import pandas as pd

#定义一个数据集
class BulldozerDataset(Dataset):
    """ 数据集演示 """
    def __init__(self, csv_file):
        """实现初始化方法，在初始化的时候将数据读载入"""
        self.df=pd.read_csv(csv_file)
    def __len__(self):
        '''
        返回df的长度
        '''
        return len(self.df)
    def __getitem__(self, idx):
        '''
        根据 idx 返回一行数据
        '''
        return self.df.iloc[idx].SalePrice

至此，我们的数据集已经定义完成了，我们可以实例化一个对象访问它

ds_demo= BulldozerDataset('median_benchmark.csv')

我们可以直接使用如下命令查看数据集数据

#实现了 __len__ 方法所以可以直接使用len获取数据总数
len(ds_demo)

#用索引可以直接访问对应的数据，对应 __getitem__ 方法
ds_demo[0]

 

 自定义的数据集已经创建好了，下面我们使用官方提供的数据载入器，读取数据

Dataloader

DataLoader为我们提供了对Dataset的读取操作，常用参数有：batch_size(每个batch的大小)、 shuffle(是否进行shuffle操作)、 num_workers(加载数据的时候使用几个子进程)。下面做一个简单的操作

dl = torch.utils.data.DataLoader(ds_demo, batch_size=10, shuffle=True, num_workers=0)

DataLoader返回的是一个可迭代对象，我们可以使用迭代器分次获取数据

idata=iter(dl)
print(next(idata))

 常见的用法是使用for循环对其进行遍历

for i, data in enumerate(dl):
    print(i,data)
    # 为了节约空间，这里只循环一遍
    break

我们已经可以通过dataset定义数据集，并使用Datalorder载入和遍历数据集，除了这些以外，PyTorch还提供能torcvision的计算机视觉扩展包，里面封装了

torchvision 包

torchvision 是PyTorch中专门用来处理图像的库，PyTorch官网的安装教程中最后的pip install torchvision 就是安装这个包。

torchvision.datasets

torchvision.datasets 可以理解为PyTorch团队自定义的dataset，这些dataset帮我们提前处理好了很多的图片数据集，我们拿来就可以直接使用：

• MNIST
• COCO
• Captions
• Detection
• LSUN
• ImageFolder
• Imagenet-12
• CIFAR
• STL10
• SVHN
• PhotoTour 我们可以直接使用，示例如下：

import torchvision.datasets as datasets
trainset = datasets.MNIST(root='./data', # 表示 MNIST 数据的加载的目录
                                      train=True,  # 表示是否加载数据库的训练集，false的时候加载测试集
                                      download=True, # 表示是否自动下载 MNIST 数据集
                                      transform=None) # 表示是否需要对数据进行预处理，none为不进行预处理

torchvision.models

torchvision不仅提供了常用图片数据集，还提供了训练好的模型，可以加载之后，直接使用，或者在进行迁移学习 torchvision.models模块的 子模块中包含以下模型结构。

• AlexNet
• VGG
• ResNet
• SqueezeNet
• DenseNet

#我们直接可以使用训练好的模型，当然这个与datasets相同，都是需要从服务器下载的
import torchvision.models as models
resnet18 = models.resnet18(pretrained=True)

torchvision.transforms

transforms 模块提供了一般的图像转换操作类，用作数据处理和数据增强

from torchvision import transforms as transforms
transform = transforms.Compose([
    transforms.RandomCrop(32, padding=4),  #先四周填充0，在把图像随机裁剪成32*32
    transforms.RandomHorizontalFlip(),  #图像一半的概率翻转，一半的概率不翻转
    transforms.RandomRotation((-45,45)), #随机旋转
    transforms.ToTensor(),
    transforms.Normalize((0.4914, 0.4822, 0.4465), (0.229, 0.224, 0.225)), #R,G,B每层的归一化用到的均值和方差
])

5.深度学习基础及数学原理

监督学习、无监督学习、半监督学习、强化学习是我们日常接触到的常见的四个机器学习方法：

• 监督学习：通过已有的训练样本（即已知数据以及其对应的输出）去训练得到一个最优模型（这个模型属于某个函数的集合，最优则表示在某个评价准则下是最佳的），再利用这个模型将所有的输入映射为相应的输出。
• 无监督学习：它与监督学习的不同之处，在于我们事先没有任何训练样本，而需要直接对数据进行建模。
• 半监督学习 ：在训练阶段结合了大量未标记的数据和少量标签数据。与使用所有标签数据的模型相比，使用训练集的训练模型在训练时可以更为准确。
• 强化学习：我们设定一个回报函数（reward function），通过这个函数来确认否越来越接近目标，类似我们训练宠物，如果做对了就给他奖励，做错了就给予惩罚，最后来达到我们的训练目的。

这里我们只着重介绍监督学习，因为我们后面的绝大部们课程都是使用的监督学习的方法，在训练和验证时输入的数据既包含输入x，又包含x对应的输出y，即学习数据已经事先给出了正确答案。

5.1线性回归

线性回归是利用数理统计中回归分析，来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法，运用十分广泛。其表达形式为y = w'x+e，e为误差服从均值为0的正态分布。

回归分析中，只包括一个自变量和一个因变量，且二者的关系可用一条直线近似表示，这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量，且因变量和自变量之间是线性关系，则称为多元线性回归分析。

简单的说： 线性回归对于输入x与输出y有一个映射f，y=f(x),而f的形式为aX+b。其中a和b是两个可调的参数，我们训练的时候就是训练a，b这两个参数。

下面我们来用PyTorch的代码来做一个详细的解释

。。。。。。。。。。。。。。。。。。。。。。。。。。。。。

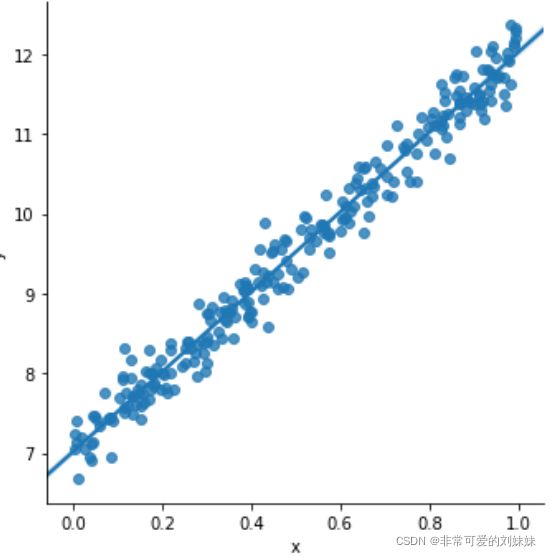
下面定义一个线性函数，这里使用 =5+7y=5x+7，这里的5和7就是上面说到的参数a和b，我们先使用matplot可视化一下这个函数

x = np.linspace(0,20,500)
y = 5*x + 7
plt.plot(x,y)

下面我生成一些随机的点，来作为我们的训练数据，加入噪声

x = np.random.rand(256)
noise = np.random.randn(256) / 4
y = x * 5 + 7 + noise
df = pd.DataFrame()
df['x'] = x
df['y'] = y

在图上显示下我们生成的数据

sns.lmplot(x='x', y='y', data=df);

 我们随机生成了一些点，下面将使用PyTorch建立一个线性的模型来对其进行拟合，这就是所说的训练的过程，由于只有一层线性模型，所以我们就直接使用了

其中参数(1, 1)代表输入输出的特征(feature)数量都是1. Linear 模型的表达式是 =⋅+y=w⋅x+b，其中  代表权重， 代表偏置

model=Linear(1, 1)

损失函数我们使用均方损失函数：MSELoss，这个后面会详细介绍

criterion = MSELoss()

优化器我们选择最常见的优化方法 SGD，就是每一次迭代计算 mini-batch 的梯度，然后对参数进行更新，学习率 0.01 ，优化器本章后面也会进行介绍

optim = SGD(model.parameters(), lr = 0.01)

训练3000次

epochs = 3000

准备训练数据: x_train, y_train 的形状是 (256, 1)， 代表 mini-batch 大小为256， feature 为1. astype('float32') 是为了下一步可以直接转换为 torch.float.

x_train = x.reshape(-1, 1).astype('float32')
y_train = y.reshape(-1, 1).astype('float32')

开始训练了

for i in range(epochs):
    # 整理输入和输出的数据，这里输入和输出一定要是torch的Tensor类型
    inputs = torch.from_numpy(x_train)
    labels = torch.from_numpy(y_train)
    #使用模型进行预测
    outputs = model(inputs)
    #梯度置0，否则会累加
    optim.zero_grad()
    # 计算损失
    loss = criterion(outputs, labels)
    # 反向传播
    loss.backward()
    # 使用优化器默认方法优化
    optim.step()
    if (i%100==0):
        #每 100次打印一下损失函数，看看效果
        print('epoch {}, loss {:1.4f}'.format(i,loss.data.item()))   

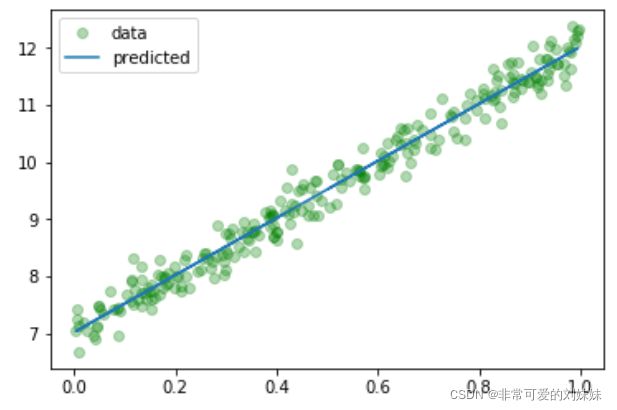
训练完成了，看一下训练的成果是多少。用 model.parameters() 提取模型参数。 ，  是我们所需要训练的模型参数 我们期望的数据 =5，=7 可以做一下对比

[w, b] = model.parameters()
print (w.item(),b.item())

再次可视化一下我们的模型，看看我们训练的数据，如果你不喜欢seaborn，可以直接使用matplot

predicted = model.forward(torch.from_numpy(x_train)).data.numpy()
plt.plot(x_train, y_train, 'go', label = 'data', alpha = 0.3)
plt.plot(x_train, predicted, label = 'predicted', alpha = 1)
plt.legend()
plt.show()

 。。。。。。。。。。。。。。。。。。。。。。。

5.1.1损失函数

损失函数（loss function）是用来估量模型的预测值(我们例子中的output)与真实值（例子中的y_train）的不一致程度，它是一个非负实值函数，损失函数越小，模型的鲁棒性就越好。 我们训练模型的过程，就是通过不断的迭代计算，使用梯度下降的优化算法，使得损失函数越来越小。损失函数越小就表示算法达到意义上的最优。

这里有一个重点：因为PyTorch是使用mini-batch来进行计算的，所以损失函数的计算出来的结果已经对mini-batch取了平均

常见（PyTorch内置）的损失函数有以下几个：

nn.L1Loss:

输入x和目标y之间差的绝对值，要求 x 和 y 的维度要一样（可以是向量或者矩阵），得到的 loss 维度也是对应一样的

nn.NLLLoss:

用于多分类的负对数似然损失函数

(,)=−[]

NLLLoss中如果传递了weights参数，会对损失进行加权，公式就变成了

nn.MSELoss:¶

均方损失函数 ，输入x和目标y之间均方差

nn.CrossEntropyLoss:

多分类用的交叉熵损失函数，LogSoftMax和NLLLoss集成到一个类中，会调用nn.NLLLoss函数，我们可以理解为CrossEntropyLoss()=log_softmax() + NLLLoss()

nn.BCELoss:

计算 x 与 y 之间的二进制交叉熵。

 5.1.2梯度下降

在介绍损失函数的时候我们已经说了，梯度下降是一个使损失函数越来越小的优化算法，在无求解机器学习算法的模型参数，即约束优化问题时，梯度下降（Gradient Descent）是最常采用的方法之一。所以梯度下降是我们目前所说的机器学习的核心，了解了它的含义，也就了解了机器学习算法的含义。

梯度

在微积分里面，对多元函数的参数求∂偏导数，把求得的各个参数的偏导数以向量的形式写出来，就是梯度。 例如函数f(x,y), 分别对x，y求偏导数，求得的梯度向量就是(∂f/∂x, ∂f/∂y)T，简称grad f(x,y)或者▽f(x,y)。

几何上讲，梯度就是函数变化增加最快的地方，沿着梯度向量的方向，更加容易找到函数的最大值。反过来说，沿着梯度向量相反的方向梯度减少最快，也就是更加容易找到函数的最小值。

我们需要最小化损失函数，可以通过梯度下降法来一步步的迭代求解，得到最小化的损失函数，和模型参数值。

梯度下降法直观解释

梯度下降法就好比下山，我们并不知道下山的路，于是决定走一步算一步，每走到一个位置的时候，求解当前位置的梯度，沿着梯度的负方向，也就是当前最陡峭的位置向下走一步，然后继续求解当前位置梯度，向这一步所在位置沿着最陡峭最易下山的位置走一步。这样一步步的走下去，一直走到觉得我们已经到了山脚。

这样走下去，有可能我们不能走到山脚，而是到了某一个局部的山峰低处（局部最优解）。

这个问题在以前的机器学习中可能会遇到，因为机器学习中的特征比较少，所以导致很可能陷入到一个局部最优解中出不来，但是到了深度学习，动辄百万甚至上亿的特征，出现这种情况的概率几乎为0，所以我们可以不用考虑这个问题。

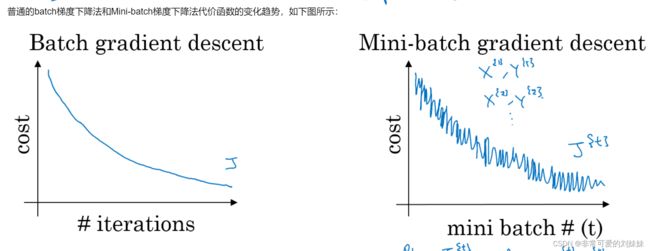
（1）Mini-batch的梯度下降法

对整个训练集进行梯度下降法的时候，我们必须处理整个训练数据集，然后才能进行一步梯度下降，即每一步梯度下降法需要对整个训练集进行一次处理，如果训练数据集很大的时候处理速度会很慢，而且也不可能一次的载入到内存或者显存中，所以我们会把大数据集分成小数据集，一部分一部分的训练，这个训练子集即称为Mini-batch。 在PyTorch中就是使用这种方法进行的训练，可以看看上一章中关于dataloader的介绍里面的batch_size就是我们一个Mini-batch的大小。

对于普通的梯度下降法，一个epoch只能进行一次梯度下降；而对于Mini-batch梯度下降法，一个epoch可以进行Mini-batch的个数次梯度下降。

• 如果训练样本的大小比较小时，能够一次性的读取到内存中，那我们就不需要使用Mini-batch，
• 如果训练样本的大小比较大时，一次读入不到内存或者现存中，那我们必须要使用 Mini-batch来分批的计算
• Mini-batch size的计算规则如下，在内存允许的最大情况下使用2的N次方个size

torch.optim是一个实现了各种优化算法的库。大部分常用优化算法都有实现，我们直接调用即可。

（2）torch.optim.SGD

随机梯度下降算法，带有动量（momentum）的算法作为一个可选参数可以进行设置，样例如下：

#lr参数为学习率，对于SGD来说一般选择0.1 0.01.0.001，如何设置会在后面实战的章节中详细说明
##如果设置了momentum，就是带有动量的SGD，可以不设置
optimizer = torch.optim.SGD(model.parameters(), lr=0.1, momentum=0.9)

（3）torch.optim.RMSprop

除了以上的带有动量Momentum梯度下降法外，RMSprop（root mean square prop）也是一种可以加快梯度下降的算法，利用RMSprop算法，可以减小某些维度梯度更新波动较大的情况，使其梯度下降的速度变得更快

#我们的课程基本不会使用到RMSprop所以这里只给一个实例
optimizer = torch.optim.RMSprop(model.parameters(), lr=0.01, alpha=0.99)

（4）torch.optim.Adam

Adam 优化算法的基本思想就是将 Momentum 和 RMSprop 结合起来形成的一种适用于不同深度学习结构的优化算法

# 这里的lr，betas，还有eps都是用默认值即可，所以Adam是一个使用起来最简单的优化方法
optimizer = torch.optim.Adam(model.parameters(), lr=0.001, betas=(0.9, 0.999), eps=1e-08)

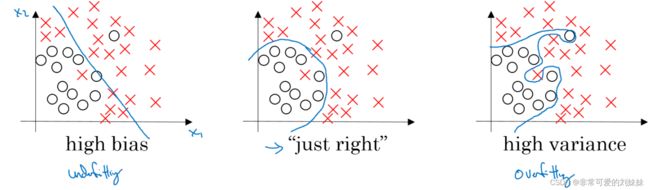
5.1.3方差/偏差

• 偏差度量了学习算法的期望预测与真实结果的偏离程序，即刻画了学习算法本身的拟合能力
• 方差度量了同样大小的训练集的变动所导致的学习性能的变化，即模型的泛化能力

从图中我们可以看出

• 高偏差（high bias）的情况，一般称为欠拟合（underfitting），即我们的模型并没有很好的去适配现有的数据，拟合度不够。
• 高方差（high variance）的情况一般称作过拟合（overfitting），即模型对于训练数据拟合度太高了，失去了泛化的能力。

如何解决这两种情况呢？

欠拟合：

• 增加网络结构，如增加隐藏层数目；
• 训练更长时间；
• 寻找合适的网络架构，使用更大的NN结构；

过拟合 ：

• 使用更多的数据；
• 正则化（ regularization）；
• 寻找合适的网络结构；

 5.1.4正则化

利用正则化来解决High variance 的问题，正则化是在 Cost function 中加入一项正则化项，惩罚模型的复杂度，这里我们简单的介绍一下正则化的概念

L1正则化

损失函数基础上加上权重参数的绝对值

L2正则化

损失函数基础上加上权重参数的平方和

需要说明的是：l1 相比于 l2 会更容易获得稀疏解

6.神经网络简介

 目前最广泛使用的定义是Kohonen于1988年的描述，神经网络是由具有适应性的简单单元组成的广泛并行互连的网络，它的组织能够模拟生物神经系统对真实世界物体所做出的交互反应。

6.1概述

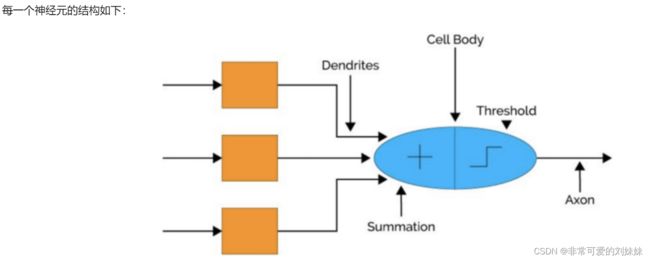
在生物神经网络中，每个神经元与其他神经元相连，当它兴奋时，就会向相连的神经元发送化学物质，从而改变这些神经元内的电位；如果某神经元的电位超过了一个阈值，那么它就会激活，即兴奋起来并向其他神经元发送化学物质。

在深度学习中也借鉴了这样的结构，每一个神经元（上面说到的简单单元）接受输入x，通过带权重w的连接进行传递，将总输入信号与神经元的阈值进行比较，最后通过激活函数处理确定是否激活，并将激活后的计算结果y输出，而我们所说的训练，所训练的就是这里面的权重w。

 6.2神经网络的表示

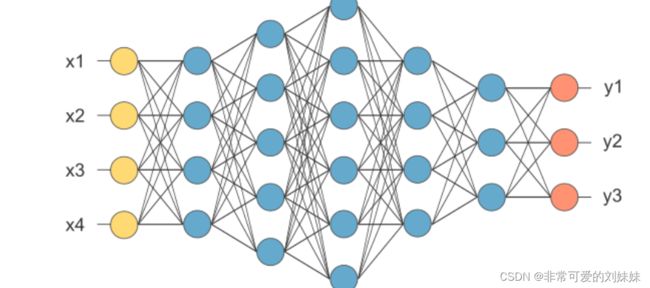
我们可以将神经元拼接起来，两层神经元，即输入层+输出层(M-P神经元)，构成感知机。 而多层功能神经元相连构成神经网络，输入层与输出层之间的所有层神经元，称为隐藏层：

如上图所示，输入层和输出层只有一个，中间的隐藏层可以有很多层（输出层也可以多个，例如经典的GoogleNet，后面会详细介绍） 

6.3激活函数

介绍神经网络的时候已经说到，神经元会对化学物质的刺激进行，当达到一定程度的时候，神经元才会兴奋，并向其他神经元发送信息。神经网络中的激活函数就是用来判断我们所计算的信息是否达到了往后面传输的条件。

在神经网络的计算过程中，每层都相当于矩阵相乘，无论神经网络有多少层输出都是输入的线性组合，就算我们有几千层的计算，无非还是个矩阵相乘，和一层矩阵相乘所获得的信息差距不大，所以需要激活函数来引入非线性因素，使得神经网络可以任意逼近任何非线性函数，这样神经网络就可以应用到众多的非线性模型中，增加了神经网络模型泛化的特性。

早期研究神经网络主要采用sigmoid函数或者tanh函数，输出有界，很容易充当下一层的输入。 近些年Relu函数及其改进型（如Leaky-ReLU、P-ReLU、R-ReLU等），由于计算简单、效果好所以在多层神经网络中应用比较多。

6.3.1sigmoid 函数

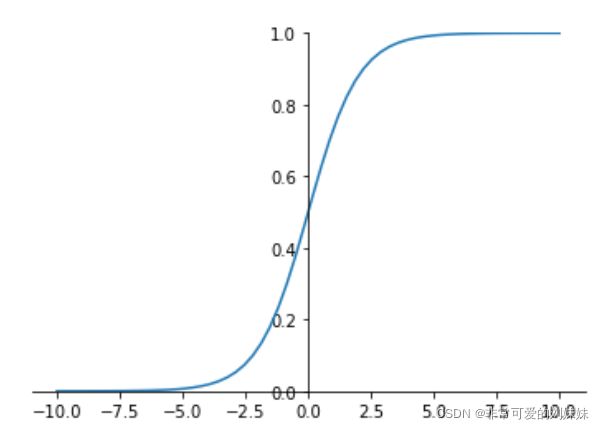
在sigmoid函数中我们可以看到，其输出是在(0,1)这个开区间，它能够把输入的连续实值变换为0和1之间的输出，如果是非常大的负数，那么输出就是0；如果是非常大的正数输出就是1，起到了抑制的作用。

但是sigmod由于需要进行指数运算（这个对于计算机来说是比较慢，相比relu），再加上函数输出不是以0为中心的（这样会使权重更新效率降低），当输入稍微远离了坐标原点，函数的梯度就变得很小了（几乎为零）。在神经网络反向传播的过程中不利于权重的优化，这个问题叫做梯度饱和，也可以叫梯度弥散。这些不足，所以现在使用到sigmod基本很少了，基本上只有在做二元分类（0，1）时的输出层才会使用。

6.3.2tanh 函数 

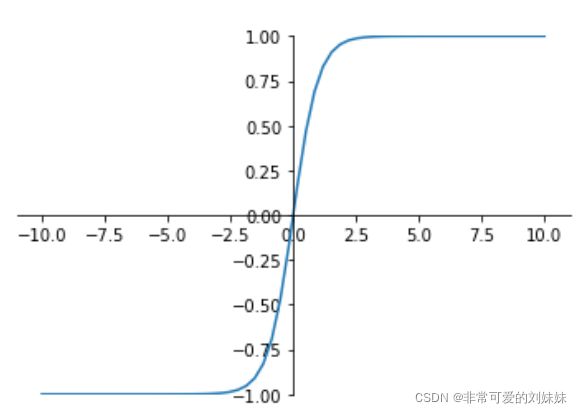
 tanh是双曲正切函数，输出区间是在(-1,1)之间，而且整个函数是以0为中心的

与sigmoid函数类似，当输入稍微远离了坐标原点，梯度还是会很小，但是好在tanh是以0为中心点，如果使用tanh作为激活函数，还能起到归一化（均值为0）的效果。

一般二分类问题中，隐藏层用tanh函数，输出层用sigmod函数，但是随着Relu的出现所有的隐藏层基本上都使用relu来作为激活函数了

6.3.3 ReLU 函数

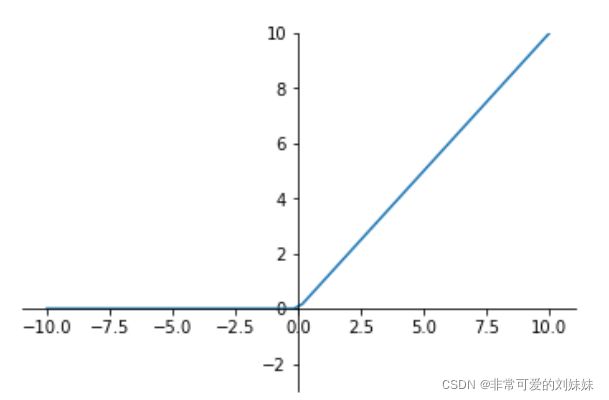
Relu（Rectified Linear Units）修正线性单元

=(0,) 导数大于0时1，小于0时0。

也就是说： z>0时，梯度始终为1，从而提高神经网络基于梯度算法的运算速度。然而当 z<0时，梯度一直为0。 ReLU函数只有线性关系（只需要判断输入是否大于0）不管是前向传播还是反向传播，都比sigmod和tanh要快很多.

 当输入是负数的时候，ReLU是完全不被激活的，这就表明一旦输入到了负数，ReLU就会死掉。但是到了反向传播过程中，输入负数，梯度就会完全到0，这个和sigmod函数、tanh函数有一样的问题。 但是实际的运用中，该缺陷的影响不是很大。

6.3.4Leaky Relu 函数

为了解决relu函数z<0时的问题出现了 Leaky ReLU函数，该函数保证在z<0的时候，梯度仍然不为0。 ReLU的前半段设为αz而非0，通常α=0.01 =(,)

理论上来讲，Leaky ReLU有ReLU的所有优点，但是在实际操作当中，并没有完全证明Leaky ReLU总是好于ReLU。

ReLU目前仍是最常用的activation function，在隐藏层中推荐优先尝试！

6.3.5深入理解前向传播和反向传播

正向传播其实就是我们的输入通过一系列的网络计算，得到̂ 的过程。

通过学习率来对训练的W和b进行更新，

=−

=−

这样反向传播就就算是完成了

7.卷积神经网络

7.1结构组成

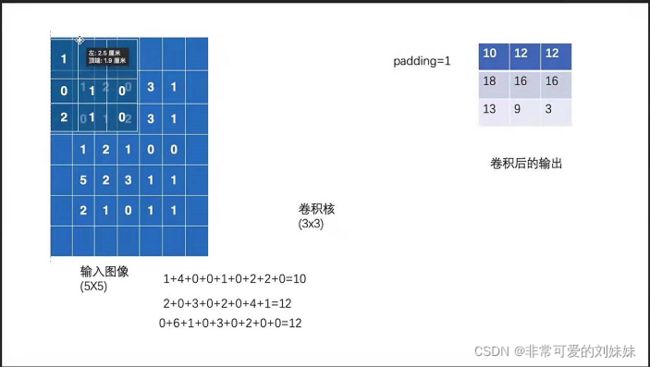
 stride=1

 

 padding=1,周围填充0

卷积层

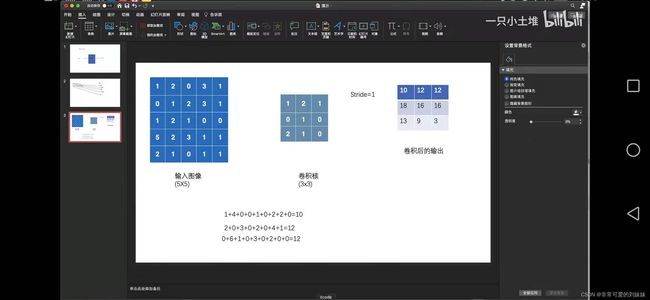
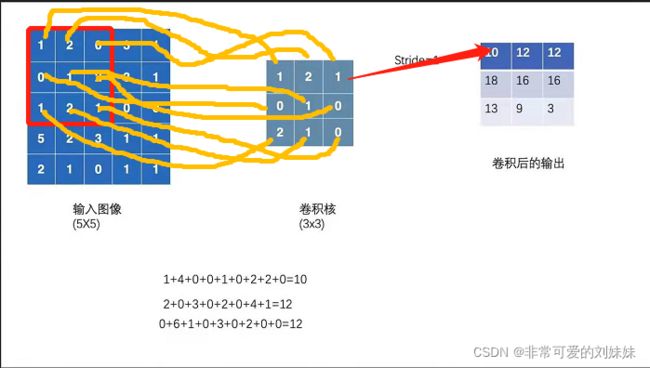
卷积核大小 f

刚才已经说到了一个重要的参数，就是核的大小，我们这里用f来表示

边界填充 (p)adding

我们看到上图，经过计算后矩阵的大小改变了，如果要使矩阵大小不改变呢，我们可以先对矩阵做一个填充，将矩阵的周围全部再包围一层，这个矩阵就变成了7*7,上下左右各加1，相当于 5+1+1=7 这时，计算的结果还是 5 * 5的矩阵，保证了大小不变，这里的p=1

步长 (s)tride

从动图上我们能够看到，每次滑动只是滑动了一个距离，如果每次滑动两个距离呢？那就需要使用步长这个参数。

计算公式

n为我们输入的矩阵的大小， 向下取整

这个公式非常重要一定要记住

卷积层

在每一个卷积层中我们都会设置多个核，每个核代表着不同的特征，这些特征就是我们需要传递到下一层的输出，而我们训练的过程就是训练这些不同的核。

激活函数

由于卷积的操作也是线性的，所以也需要进行激活，一般情况下，都会使用relu。

池化层（pooling）

池化层是CNN的重要组成部分，通过减少卷积层之间的连接，降低运算复杂程度，池化层的操作很简单，就想相当于是合并，我们输入一个过滤器的大小，与卷积的操作一样，也是一步一步滑动，但是过滤器覆盖的区域进行合并，只保留一个值。 合并的方式也有很多种，例如我们常用的两种取最大值maxpooling，取平均值avgpooling

池化层的输出大小公式也与卷积层一样，由于没有进行填充，所以p=0，可以简化为 

dropout层

dropout是2014年 Hinton 提出防止过拟合而采用的trick，增强了模型的泛化能力 Dropout（随机失活）是指在深度学习网络的训练过程中，按照一定的概率将一部分神经网络单元暂时从网络中丢弃，相当于从原始的网络中找到一个更瘦的网络，说的通俗一点，就是随机将一部分网络的传播掐断，听起来好像不靠谱，但是通过实际测试效果非常好。 有兴趣的可以去看一下原文Dropout: A Simple Way to Prevent Neural Networks from Overfitting这里就不详细介绍了。

全连接层

全链接层一般是作为最后的输出层使用，卷积的作用是提取图像的特征，最后的全连接层就是要通过这些特征来进行计算，输出我们所要的结果了，无论是分类，还是回归。

我们的特征都是使用矩阵表示的，所以再传入全连接层之前还需要对特征进行压扁，将他这些特征变成一维的向量，如果要进行分类的话，就是用sofmax作为输出，如果要是回归的话就直接使用linear即可。

7.2.循环神经网络

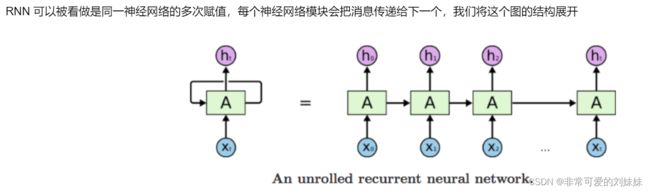
循环神经网络的基本结构特别简单，就是将网络的输出保存在一个记忆单元中，这个记忆单元和下一次的输入一起进入神经网络中。我们可以看到网络在输入的时候会联合记忆单元一起作为输入，网络不仅输出结果，还会将结果保存到记忆单元中

循环神经网络具有特别好的记忆特性，能够将记忆内容应用到当前情景下，但是网络的记忆能力并没有想象的那么有效。记忆最大的问题在于它有遗忘性，我们总是更加清楚地记得最近发生的事情而遗忘很久之前发生的事情，循环神经网络同样有这样的问题。

pytorch 中使用 nn.RNN 类来搭建基于序列的循环神经网络，它的构造函数有以下几个参数：

• input_size：输入数据X的特征值的数目。
• hidden_size：隐藏层的神经元数量，也就是隐藏层的特征数量。
• num_layers：循环神经网络的层数，默认值是 1。
• bias：默认为 True，如果为 false 则表示神经元不使用 bias 偏移参数。
• batch_first：如果设置为 True，则输入数据的维度中第一个维度就是 batch 值，默认为 False。默认情况下第一个维度是序列的长度， 第二个维度才是 - - batch，第三个维度是特征数目。
• dropout：如果不为空，则表示最后跟一个 dropout 层抛弃部分数据，抛弃数据的比例由该参数指定。

RNN 中最主要的参数是 input_size 和 hidden_size，这两个参数务必要搞清楚。其余的参数通常不用设置，采用默认值就可以了。

 RNN其实也是一个普通的神经网络，只不过多了一个 hidden_state 来保存历史信息。这个hidden_state的作用就是为了保存以前的状态，我们常说RNN中保存的记忆状态信息，就是这个 hidden_state 。

这个公式里面的  是我们当前状态的输入值，ℎ(−1) 就是上面说的要传入的上一个状态的hidden_state，也就是记忆部分。 整个网络要训练的部分就是 ℎ 当前状态输入值的权重，ℎℎhidden_state也就是上一个状态的权重还有这两个输入偏置值。这四个值加起来使用tanh进行激活，pytorch默认是使用tanh作为激活，也可以通过设置使用relu作为激活函数。

 

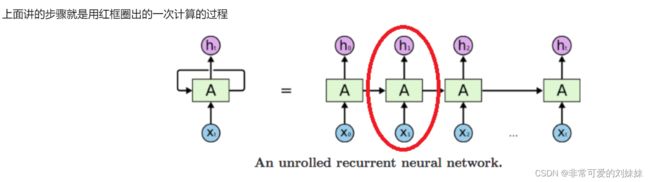
 这个步骤与普通的神经网络没有任何的区别，而 RNN 因为多了 序列（sequence） 这个维度，要使用同一个模型跑 n 次前向传播，这个n就是我们序列设置的个数。

7.3LSTM

这个步骤与普通的神经网络没有任何的区别，而 RNN 因为多了 序列（sequence） 这个维度，要使用同一个模型跑 n 次前向传播，这个n就是我们序列设置的个数。

标准的循环神经网络内部只有一个简单的层结构，而 LSTM 内部有 4 个层结构：

第一层是个忘记层：决定状态中丢弃什么信息

第二层tanh层用来产生更新值的候选项，说明状态在某些维度上需要加强，在某些维度上需要减弱

第三层sigmoid层（输入门层），它的输出值要乘到tanh层的输出上，起到一个缩放的作用，极端情况下sigmoid输出0说明相应维度上的状态不需要更新

最后一层决定输出什么，输出值跟状态有关。候选项中的哪些部分最终会被输出由一个sigmoid层来决定。

pytorch 中使用 nn.LSTM 类来搭建基于序列的循环神经网络，他的参数基本与RNN类似，这里就不列出了。

7.4.GRU

GRU 和 LSTM 最大的不同在于 GRU 将遗忘门和输入门合成了一个"更新门"，同时网络不再额外给出记忆状态，而是将输出结果作为记忆状态不断向后循环传递，网络的输人和输出都变得特别简单。

7.5循环网络的向后传播（BPTT）

在向前传播的情况下，RNN的输入随着每一个时间步前进。在反向传播的情况下，我们“回到过去”改变权重，因此我们叫它通过时间的反向传播（BPTT）。

我们通常把整个序列（单词）看作一个训练样本，所以总的误差是每个时间步（字符）中误差的和。权重在每一个时间步长是相同的（所以可以计算总误差后一起更新）。

1. 使用预测输出和实际输出计算交叉熵误差
2. 网络按照时间步完全展开
3. 对于展开的网络，对于每一个实践步计算权重的梯度
4. 因为对于所有时间步来说，权重都一样，所以对于所有的时间步，可以一起得到梯度（而不是像神经网络一样对不同的隐藏层得到不同的梯度）
5. 随后对循环神经元的权重进行升级

RNN展开的网络看起来像一个普通的神经网络。反向传播也类似于普通的神经网络，只不过我们一次得到所有时间步的梯度。如果有100个时间步，那么网络展开后将变得非常巨大，所以为了解决这个问题才会出现LSTM和GRU这样的结构。

7.6词嵌入（word embedding）

用不同的特征来对各个词汇进行表征，相对与不同的特征，不同的单词均有不同的值这就是词嵌入。

词嵌入不仅对不同单词实现了特征化的表示，还能通过计算词与词之间的相似度，实际上是在多维空间中，寻找词向量之间各个维度的距离相似度，我们就可以实现类比推理，比如说夏天和热，冬天和冷，都是有关联关系的。

在 PyTorch 中我们用 nn.Embedding 层来做嵌入词袋模型，Embedding层第一个输入表示我们有多少个词，第二个输入表示每一个词使用多少维度的向量表示。

7.7Beam search

在生成第一个词的分布后，可以使用贪心搜索会根据我们的条件语言模型挑选出最有可能输出的第一个词语，但是对于贪心搜索算法来说，我们的单词库中有成百到千万的词汇，去计算每一种单词的组合的可能性是不可行的。所以我们使用近似的搜索办法，使得条件概率最大化或者近似最大化的句子，而不是通过单词去实现。

Beam Search（集束搜索）是一种启发式图搜索算法，通常用在图的解空间比较大的情况下，为了减少搜索所占用的空间和时间，在每一步深度扩展的时候，剪掉一些质量比较差的结点，保留下一些质量较高的结点。虽然Beam Search算法是不完全的，但是用于了解空间较大的系统中，可以减少空间占用和时间。

Beam search可以看做是做了约束优化的广度优先搜索，首先使用广度优先策略建立搜索树，树的每层，按照启发代价对节点进行排序，然后仅留下预先确定的个数（Beam width-集束宽度）的节点，仅这些节点在下一层次继续扩展，其他节点被剪切掉。

1. 将初始节点插入到list中
2. 将给节点出堆，如果该节点是目标节点，则算法结束；
3. 否则扩展该节点，取集束宽度的节点入堆。然后到第二步继续循环。
4. 算法结束的条件是找到最优解或者堆为空。

在使用上，集束宽度可以是预先约定的，也可以是变化的，具体可以根据实际场景调整设定。

7.8注意力模型

对于使用编码和解码的RNN模型，我们能够实现较为准确度机器翻译结果。对于短句子来说，其性能是十分良好的，但是如果是很长的句子，翻译的结果就会变差。 我们人类进行人工翻译的时候，都是一部分一部分地进行翻译，引入的注意力机制，和人类的翻译过程非常相似，其也是一部分一部分地进行长句子的翻译。