平衡二叉树

目录

一、介绍

二、平衡二叉树的旋转

（一）单旋的情况

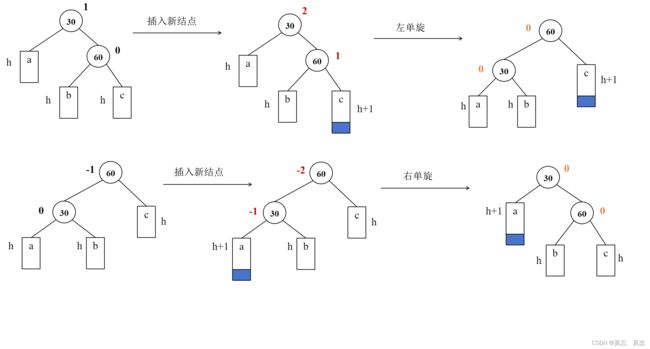
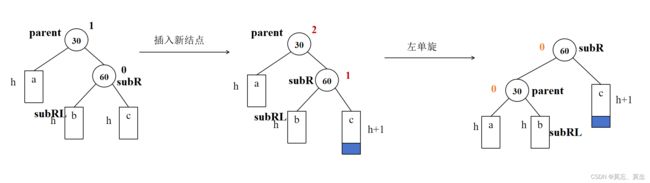
1. 左单旋

2. 右单旋

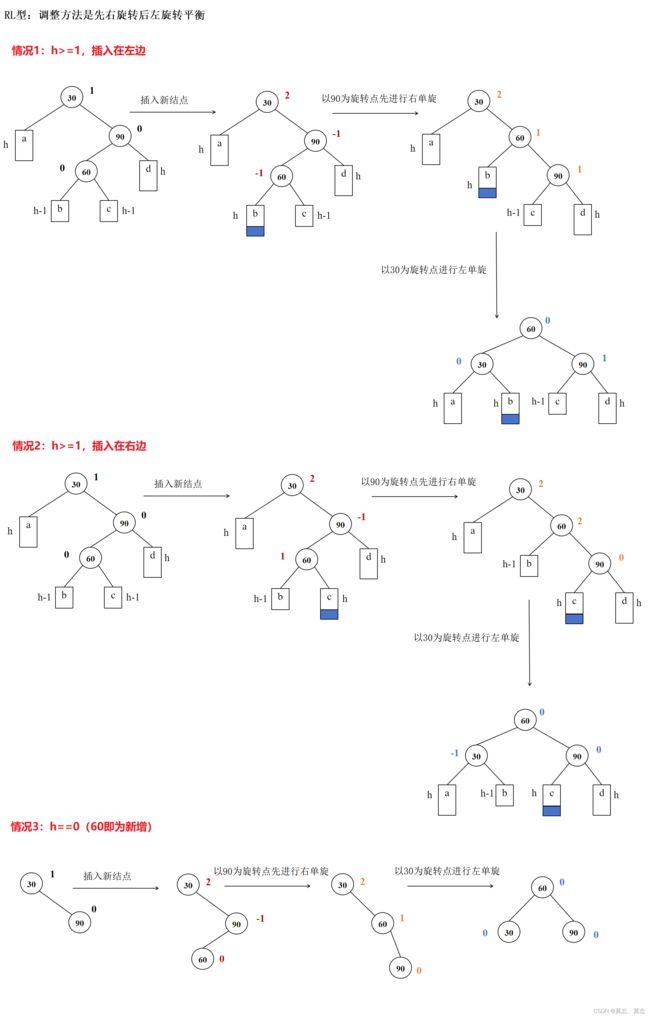
（二）RL双旋

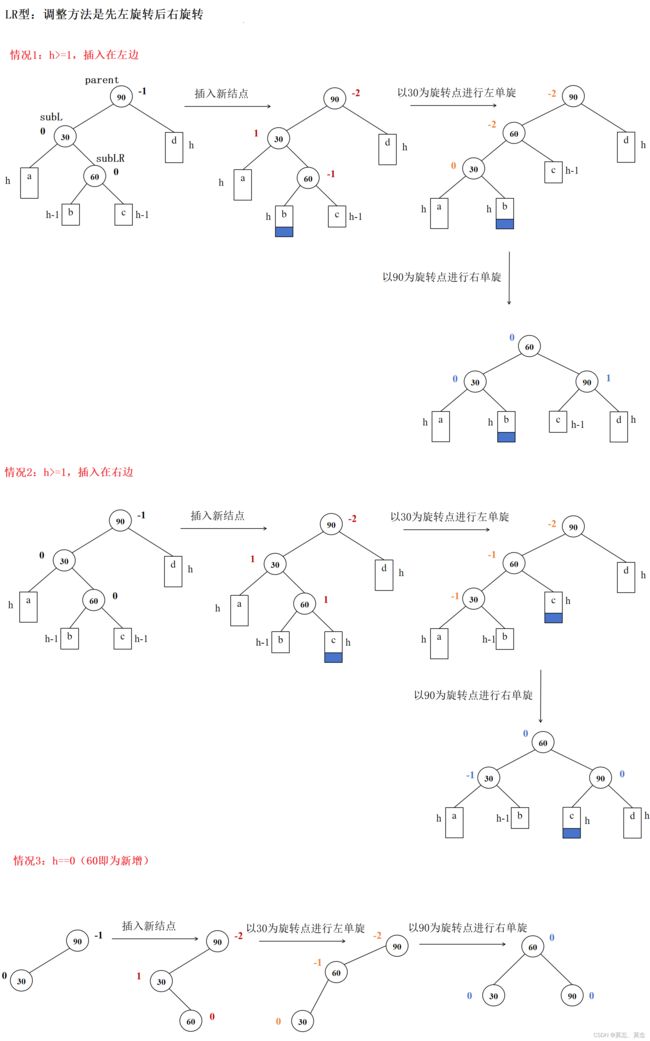
（三）LR双旋

三、完整代码

1. 测试用例1

2. 测试用例2

3. 测试用例3

---

一、介绍

• 平衡二叉树：又称AVL树，它或是一棵空树，或是左子树和右子树都是平衡二叉树且左右子树的高度之差的绝对值不超过1的二叉树 。
• 注意：二叉排序树不一定是平衡二叉树

二、平衡二叉树的旋转

（一）单旋的情况

1. 左单旋

void RotateL(Node* parent)//左单旋
{
	Node* parentParent = parent->_parent;
	Node* subR = parent->_right;
	Node* subRL = subR->_left;

	parent->_right = subRL;
	subR->_left = parent;

	//更新调整结点的父指针指向
	parent->_parent = subR;
	//subRL->_parent = parent;错误，没有判断subRL是不是为空
	if (subRL != nullptr)
	{
		subRL->_parent = parent;
	}

	if (_root == parent)
	{
		_root = subR;
		subR->_parent = nullptr;
	}
	else
	{
		if (parentParent->_left == parent)
		{
			parentParent->_left = subR;
		}
		else
		{
			parentParent->_right = subR;
		}
		subR->_parent = parentParent;
	}

	//更新平衡因子
	parent->_bf = subR->_bf = 0;
}

2. 右单旋

void RotateR(Node* parent)//右单旋
{
	Node* parentParent = parent->_parent;
	Node* subL = parent->_left;
	Node* subLR = subL->_right;

	parent->_left = subLR;
	//更新调整结点的父指针指向
	if (subLR != nullptr)
	{
		subLR->_parent = parent;
	}

	subL->_right = parent;
	//更新调整结点的父指针指向
	parent->_parent = subL;


	if (_root == parent)
	{
		_root = subL;
		subL->_parent = nullptr;
	}
	else
	{
		//需要先判断subR应该链接在parentParent的哪一侧
		if (parentParent->_left == parent)
		{
			parentParent->_left = subL;
		}
		else
		{
			parentParent->_right = subL;
		}
		subL->_parent = parentParent;
	}
	//更新平衡因子
	parent->_bf = subL->_bf = 0;
}

（二）RL双旋

void RotateRL(Node* parent)//先右旋再左旋
{
	//1.旋转之前先记录下平衡因子
	Node* subR = parent->_right;
	Node* subRL = subR->_left;
	int oldbf = subRL->_bf;

	//2.进行旋转，先右旋，再左旋
	RotateR(subR);
	RotateL(parent);

	//3.更新平衡因子
	if (oldbf == 0)//说明subRL自己就是新增
	{
		parent->_bf = subR->_bf = subRL->_bf = 0;
	}
	else if (oldbf == -1)//说明插在了subRL的左边
	{
		parent->_bf = 0;
		subR->_bf = 1;
		subRL->_bf = 0;
	}
	else if (oldbf == 1)
	{
		parent->_bf = -1;
		subR->_bf = 0;
		subRL->_bf = 0;
	}
	else
	{
		assert(false);
	}
}

（三）LR双旋

void RotateLR(Node* parent)//先左旋再右旋
{
	//1.旋转之前先记录下平衡因子
	Node* subL = parent->_left;
	Node* subLR = subL->_right;
	int oldbf = subLR->_bf;

	//2.进行旋转，先左旋，后右旋
	RotateL(subL);
	RotateR(parent);

	//3.更新平衡因子
	if (oldbf == 0)//自己是新增
	{
		parent->_bf = subL->_bf = subLR->_bf = 0;
	}
	else if (oldbf == -1)//说明插在了subL的左边
	{
		parent->_bf = 1;
		subL->_bf = 0;
		subLR->_bf = 0;
	}
	else if (oldbf == 1)//说明插在了subL的右边
	{
		parent->_bf = 0;
		subL->_bf = -1;
		subLR->_bf = 0;
	}
	else
	{
		assert(false);
	}
}

三、完整代码

#pragma once
#include
#include
#include
using namespace std;
//结点类
template
struct AVLTreeNode
{
	AVLTreeNode* _right;
	AVLTreeNode* _left;
	AVLTreeNode* _parent;
	pair _kv;

	int _bf;//平衡因子

	AVLTreeNode(const pair& kv)//构造函数
		:_right(nullptr)
		, _left(nullptr)
		, _parent(nullptr)
		, _kv(kv)
		, _bf(0)
	{}
};

//平衡二叉树
template
class AVLTree
{
	typedef AVLTreeNode Node;
public:
	void RotateL(Node* parent)//左单旋
	{
		Node* parentParent = parent->_parent;
		Node* subR = parent->_right;
		Node* subRL = subR->_left;

		parent->_right = subRL;
		subR->_left = parent;

		//更新调整结点的父指针指向
		parent->_parent = subR;
		//subRL->_parent = parent;错误，没有判断subRL是不是为空
		if (subRL != nullptr)
		{
			subRL->_parent = parent;
		}

		if (_root == parent)
		{
			_root = subR;
			subR->_parent = nullptr;
		}
		else
		{
			if (parentParent->_left == parent)
			{
				parentParent->_left = subR;
			}
			else
			{
				parentParent->_right = subR;
			}
			subR->_parent = parentParent;
		}

		//更新平衡因子
		parent->_bf = subR->_bf = 0;
	}
	void RotateR(Node* parent)//右单旋
	{
		Node* parentParent = parent->_parent;
		Node* subL = parent->_left;
		Node* subLR = subL->_right;

		parent->_left = subLR;
		//更新调整结点的父指针指向
		if (subLR != nullptr)
		{
			subLR->_parent = parent;
		}

		subL->_right = parent;
		//更新调整结点的父指针指向
		parent->_parent = subL;


		if (_root == parent)
		{
			_root = subL;
			subL->_parent = nullptr;
		}
		else
		{
			//需要先判断subR应该链接在parentParent的哪一侧
			if (parentParent->_left == parent)
			{
				parentParent->_left= subL;
			}
			else
			{
				parentParent->_right = subL;
			}
			subL->_parent = parentParent;
		}
		//更新平衡因子
		parent->_bf = subL->_bf = 0;
	}
	void RotateRL(Node* parent)//先右旋再左旋
	{
		//1.旋转之前先记录下平衡因子
		Node* subR = parent->_right;
		Node* subRL = subR->_left;
		int oldbf = subRL->_bf;

		//2.进行旋转，先右旋，再左旋
		RotateR(subR);
		RotateL(parent);

		//3.更新平衡因子
		if (oldbf == 0)//说明subRL自己就是新增
		{
			parent->_bf = subR->_bf = subRL->_bf = 0;
		}
		else if (oldbf == -1)//说明插在了subRL的左边
		{
			parent->_bf = 0;
			subR->_bf = 1;
			subRL->_bf = 0;
		}
		else if (oldbf == 1)
		{
			parent->_bf = -1;
			subR->_bf = 0;
			subRL->_bf = 0;
		}
		else
		{
			assert(false);
		}
	}
	void RotateLR(Node* parent)//先左旋再右旋
	{
		//1.旋转之前先记录下平衡因子
		Node* subL = parent->_left;
		Node* subLR = subL->_right;
		int oldbf = subLR->_bf;

		//2.进行旋转，先左旋，后右旋
		RotateL(subL);
		RotateR(parent);

		//3.更新平衡因子
		if (oldbf == 0)//自己是新增
		{
			parent->_bf = subL->_bf = subLR->_bf = 0;
		}
		else if (oldbf == -1)//说明插在了subL的左边
		{
			parent->_bf = 1;
			subL->_bf = 0;
			subLR->_bf = 0;
		}
		else if (oldbf == 1)//说明插在了subL的右边
		{
			parent->_bf = 0;
			subL->_bf = -1;
			subLR->_bf = 0;
		}
		else
		{
			assert(false);
		}	
	}

	bool Insert(const pair& kv)
	{
		if (_root == nullptr)//根节点本身为空
		{
			_root = new Node(kv);
			return true;
		}

		//_root不为空的时候，需要查找
		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (kv.first > cur->_kv.first)
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (kv.first < cur->_kv.first)
			{
				parent = cur;
				cur = cur->_left;
			}
			else
			{
				return false;
			}
		}

		//链接
		cur = new Node(kv);
		if (kv.first > parent->_kv.first)
		{
			parent->_right = cur;
			cur->_parent = parent;
		}
		else
		{
			parent->_left = cur;
			cur->_parent = parent;
		}

		//旋转
		while (parent)
		{
			if (cur == parent->_left)//插入在左边，平衡因子-1
			{
				parent->_bf--;
			}
			else//插入在右边，平衡因子+1
			{
				parent->_bf++;
			}


			//更新后检查平衡因子
			if (parent->_bf == 0)//插入结点以后，父结点的平衡因子为0，说明仍然平衡，不用更新了
			{
				break;
			}
			else if (parent->_bf == 1 || parent->_bf == -1)//插入结点以后，父结点的平衡因子为1或者-1，说明需要向上更新
			{
				cur = parent;
				parent = parent->_parent;
			}
			else if (parent->_bf == 2 || parent->_bf == -2)
			{
				if (parent->_bf == 2 && cur->_bf == 1)//需要进行左旋的情况
				{
					RotateL(parent);
				}
				else if (parent->_bf == -2 && cur->_bf == -1)//需要进行右旋的情况
				{
					RotateR(parent);
				}
				else if (parent->_bf == 2 && cur->_bf == -1)//RL型
				{
					RotateRL(parent);
				}
				else if (parent->_bf == -2 && cur->_bf == 1)//LR型
				{
					RotateLR(parent);
				}
				break;
			}
			else
			{
				assert(false);
			}
		}
		return true;//成功退出
	}


	void InOrder()//中序遍历
	{
		_InOrder(_root);
		cout << endl;
	}
	void _InOrder(Node* root)//中序遍历
	{
		if (root == nullptr)
		{
			return;
		}

		_InOrder(root->_left);
		cout << root->_kv.first << " ";
		_InOrder(root->_right);
	}

	int _Height(Node* root)
	{
		if (root == nullptr)
		{
			return 0;
		}

		int left = _Height(root->_left);
		int right = _Height(root->_right);
		return left > right ? (left + 1) : (right + 1);
	}

	bool IsBalance()
	{
		return _IsBalance(_root);
	}

	bool _IsBalance(Node* root)
	{
		if (root == nullptr)
			return true;

		int leftHeight = _Height(root->_left);
		int rightHeight = _Height(root->_right);
		if (rightHeight - leftHeight != root->_bf)
		{
			cout << root->_kv.first << "平衡因子异常" << endl;
			return false;
		}
		//归检查是否平衡
		return abs(rightHeight - leftHeight) < 2
			&& _IsBalance(root->_left)
			&& _IsBalance(root->_right);
	}

private:
	Node* _root = nullptr;
};

1. 测试用例1

#include"AVLTree.h"

int main()
{
	int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };

//                4
//          /           \
//         2             6
//      /     \       /      \
//     1       3      5      15
//                         /    \
//                        7      16
//                         \
//                          14

//                4
//          /           \
//         2             7
//      /     \       /      \
//     1       3     6       15
//                  /       /   \
//                 5       14    16
//                         



	AVLTree t;
	for (auto e : a)
	{
		t.Insert(pair(e, e));
	}
	t.InOrder();

	// 检查是否平衡
	if (t.IsBalance())
	{
		cout << "已经平衡!" << endl;
	}
	return 0;
}

2. 测试用例2

#include"AVLTree.h"

int main()
{
	int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };

	AVLTree t;
	for (auto e : a)
	{
		t.Insert(pair(e, e));
	}
	t.InOrder();

	// 检查是否平衡
	if (t.IsBalance())
	{
		cout << "已经平衡!" << endl;
	}
	return 0;
}

3. 测试用例3

#include"AVLTree.h"

int main()
{
	const int N = 30;
	vector v;
	v.reserve(N);
	//srand(time(0));

	for (size_t i = 0; i < N; i++)
	{
		v.push_back(rand());
		cout << v.back() << endl;
	}

	AVLTree t;
	for (auto e : v)
	{
		if (e == 14604)
		{
			int x = 0;
		}

		t.Insert(make_pair(e, e));
		cout << "Insert:" << e << "->" << t.IsBalance() << endl;
	}

	// 检查是否平衡
	if (t.IsBalance())
	{
		cout << "已经平衡!" << endl;
	}
	return 0;
}