LeetCode刷题总结——并查集

并查集

并查集的引入

并查集的核心思想是$用集和中的一个元素来代表这个集和$,相信大家肯定玩过球球大作战或者贪吃蛇大作战吧，为了方便理解，我们把这个集和比作为此刻你的蛇的总体，代表元素是蛇头，规则很简单，两个蛇如果相遇，则大蛇吃掉小蛇(不考虑蛇头撞到蛇身哈，只判断大小就好)，这时候，从并查集的角度理解，大蛇合并了小蛇，这时候大蛇的代表了大蛇和小蛇

这个过程叫做并查集的$合并$,那对于一个集和来说，必不可少的就是$查询$某个元素是属于哪个集和的

因为我们是用集和的代表元素来表示这个集和的，所以查询的结果就是这个代表元素

基于上面的描述，我们可以写出并查集的原始版本

初始化

vector<int> parent(MAX_N)
void init(int n){
    for(int i=0;i<n;i++){
        parent[i]=i;
    }
}

查询

int query(int index){
    //若当前元素就是代表元素
    if(index==parent[index]){
        return index;
    }
    //递归查找代表元素
    return query(parent[index]);
    
}

合并

void merge(int a,int b){
    parent[find(a)]=find(b);
}

对于最原始的并查集，在find函数中一个集和当中的元素的排列是成链状的

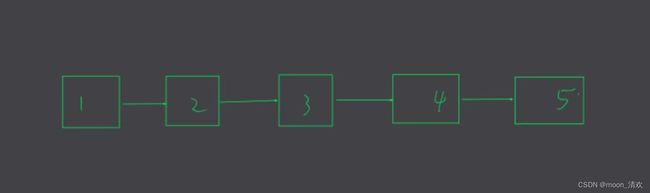
这种情况下，我们要查询一个元素，平均要递归很多次，很显然在处理大数据不合适，而产生这种情况的根本原因是我们是一层一层的将元素加进去的，所以元素的代表元素永远是他的前一个元素，而最快的形式一定是，$集和当中的元素直接指向代表元素$,类似于古代农民直接面见皇上，而不需要通过县令，知府…

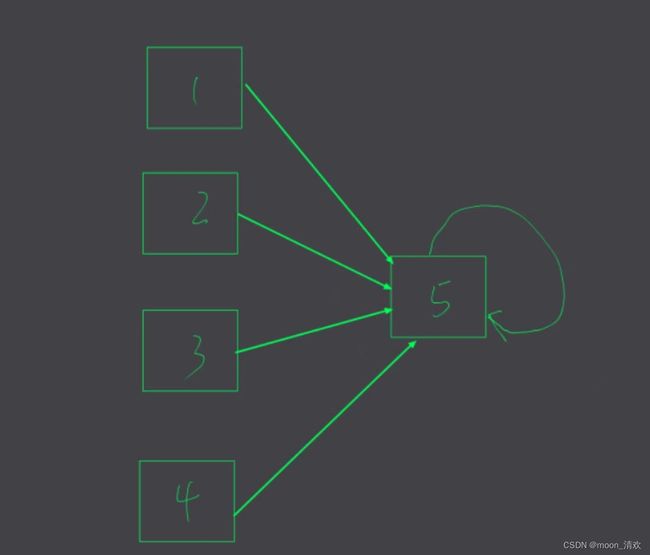
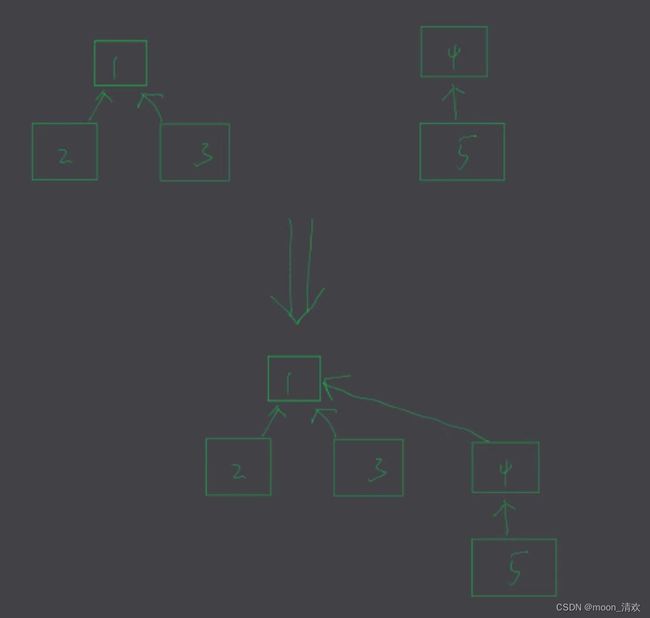
要实现这种直接指向，我们可以考虑一种情况

假设，我们我们在原始的find函数中建立了4->5的连接，这时候我们需要把3加进去，我们只需要令parent[3]=find(parent[3]);这样就建立了节点3直接指向5的效果，这个过程叫做$路径压缩$

查找(路径压缩)

int find(int a){
    if(a==parent[a]){
        return a;
    }else{
        parent[a]=find(praent[a]);
    }
    return parent[a];
}

但是要注意的一点是，由于在并查集的合并很复杂，所以进行路径压缩得到的图，不一定都是直接连接的，因为$由于路径压缩只在查询时进行，也只压缩一条路径$

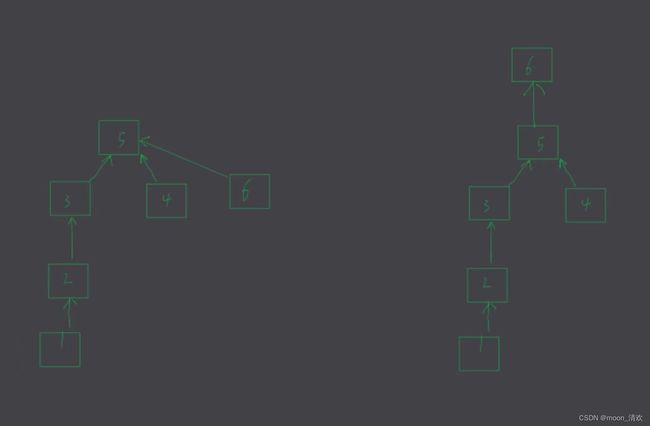
所以我们不会得到一个深度为2的树，但是我们仍旧想让最后形成的这棵树的深度变底，这可以减少递归次数，提高查询效率

例如我们需要将5和6合并，会有两种方案

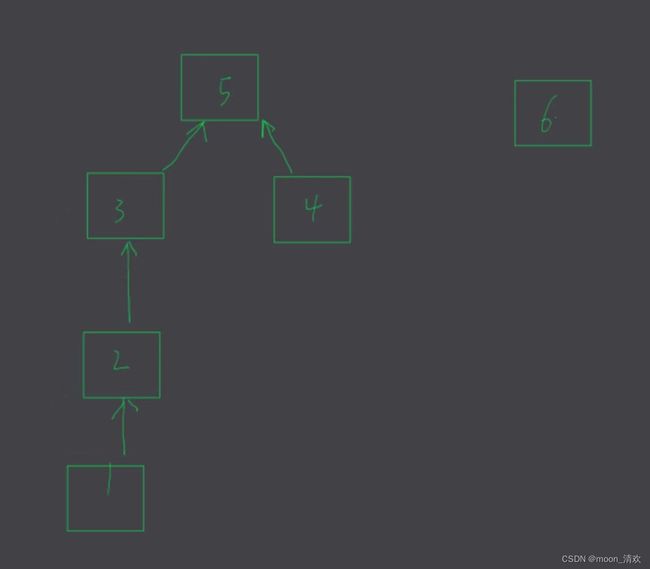
显然左边的树要比树的深度小，所以我们应该让parent[6]=5

要实现这种连接，我们需要定义一个数组rank，用来保存每个树的高度，也就是秩，然后在进行连接的时候需要将$秩小的指向秩大的$,

初始化

vector<int> parent(MAX_N);
vector<int> rank(MAX_N);
void init(int n){
    for(int i=0;i<n;i++){
        parent[i]=i;
        rank[i]=1;
    }
}

合并 按秩合并

void merge(int a,int b){
    int fa=find(a);
    int fb=find(b);
    if(fa==fb){
        return;
    }
    if(rank[fa]<=rank[fb]){
        parent[fa]=fb;
    }else{
        parnet[fb]=fa;
    }
    //如果深度相同，则在新节点的rank加1
    if(rank[fa]==rank[fb]&&fa!=fb){
        rank[fb]++;
    }
    return;
}

为什么深度一样时需要加1，画图可以很好理解

并查集的作用

主要是用来判断两个元素是否属于一个集和，用来判断是否成环，连通性问题，二分图问题

比较典型的问题如下

1.岛屿数量

2.判断二分图

3.交换字符串的元素

4.连接所有点的最小费用

5.除法求值

并查集的应用

1.岛屿数量

题目描述

给你一个由 ‘1’（陆地）和 ‘0’（水）组成的的二维网格，请你计算网格中岛屿的数量。

岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。

此外，你可以假设该网格的四条边均被水包围。

思路

将该二维网络一维化，逐次遍历，将上下左右的1全部合并在一起，最终，我们只需要在1的时候，求出代表元素恰好等于他本身的元素的个数，就相当于最终剩余了多少条蛇

代码

class Solution {
public:
    int query(vector<int>&parent,int index){
        if(parent[index]!=index){
            parent[index]=query(parent,parent[index]);
        }
        return parent[index];
    }
    void merge(vector<int>&parent,vector<int>&rank,int a,int b){
        int fa=query(parent,a);
        int fb=query(parent,b);
        if(fa==fb){
            return;
        }
        if(rank[fa]<=rank[fb]){
            parent[fa]=fb;
        }else{
            parent[fb]=fa;
        }
        if(rank[fa]==rank[fb]){
            rank[fb]++;
        }
        return;
    }
    int numIslands(vector<vector<char>>& grid) {
        int n=grid.size();
        int m=grid[0].size();
        vector<int> parent(n*m);
        vector<int> rank(n*m);
        for(int i=0;i<n*m;i++){
            parent[i]=i;
            rank[i]=1;
        }
        for(int i=0;i<n;i++){
            for(int j=0;j<m;j++){
                int idx=i*m+j;
                if(grid[i][j]=='1'){
                    if(i<n-1&&grid[i+1][j]=='1'){
                        merge(parent,rank,idx,idx+m);
                    }
                    if(j<m-1&&grid[i][j+1]=='1'){
                        merge(parent,rank,idx,idx+1);
                    }
                }
            }
        }
        int ans=0;
        for(int i=0;i<n;i++){
            for(int j=0;j<m;j++){
                int idx=i*m+j;
                if(grid[i][j]=='1'&&query(parent,idx)==idx){
                    ans++;
                }
            }
        }
        return ans;
    }
};

细节

利用idx=i*m+j来代表当前点的位置，可以方便的求出临近点的坐标值

2.判断二分图

题目描述

存在一个 无向图 ，图中有 n 个节点。其中每个节点都有一个介于 0 到 n - 1 之间的唯一编号。给你一个二维数组 graph ，其中 graph[u] 是一个节点数组，对于graph[u]中的任意元素v,都表示u和v有一条无向边

二分图 定义：如果能将一个图的节点集合分割成两个独立的子集 A 和 B ，并使图中的每一条边的两个节点一个来自 A 集合，一个来自 B 集合，就将这个图称为 二分图 。

如果图是二分图，返回 true ；否则，返回 false

思路

题目的意思是想让我们将这个无向图分成两个图，分别为图A和图B，其中图A和图B中的边，在原图中不能出现，也就是$在原图中相邻的点，在分开的图中不能相连$,

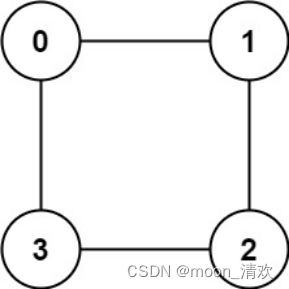
我们对任意一个graph[u]来分析，假设graph[0]={1,2,3}；

那么，原图存在了三条边

0->1

0->2

0->3

而这三条件不能在分开之后的图中出现

所以我们将1，2，3连接起来

将0单独连接起来

这样是保证二分图正确性的唯一做法

那怎么判断这个是不是二分图呢，当我们将所有边连接完毕后，我们$再次测试graph[u]当中的元素和u的连通性$，如果连通了，说明不能成为二分图，直接返回false，遍历结束后返回true

代码

class Solution {
public:
    int query(vector<int>&parent,int index){
        if(parent[index]!=index){
            parent[index]=query(parent,parent[index]);
        }
        return parent[index];
    }
    void merge(vector<int>&parent,vector<int>&rank,int a,int b){
        int fa=query(parent,a);
        int fb=query(parent,b);
        if(fa==fb){
            return;
        }
        if(rank[fa]<=rank[fb]){
            parent[fa]=fb;
        }else{
            parent[fb]=fa;
        }
        if(rank[fa]==rank[fb]){
            rank[fb]++;
        }
        return;
    }
    bool isBipartite(vector<vector<int>>& graph) {
		int n=graph.size();
        vector<int> parent(n);
        vector<int> rank(n);
        for(int i=0;i<n;i++){
            parent[i]=i;
            rank[i]=1;
        }
        for(int i=0;i<n;i++){
            if(graph[i].size()==0){
                continue;
            }
            int v=graph[i][0];
            for(int j=1;j<graph[i].size();j++){
                merge(parent,rank,v,graph[i][j]);
            }
        }
        for(int i=0;i<n;i++){
            for(int j=0;j<graph[i].size();j++){
                if(query(parent,i)==query(parent,graph[i][j])){
                    return false;
                }
            }
        }
        return true;
    }
};

3.交换字符串的元素

题目描述

给你一个字符串 s，以及一个数组 pairs，其中 pairs[i] = [a, b] 表示s[a]和s[b]可以进行任意次数的交换，求交换之后字典序最小的情况

思路

我们先定义一个$好字符串$,好字符串的定义如下 好字符串的所以字符均可以$相互交换$,所以我们要得到好字符串的最小字典序，就是将该好字符串排序即可

那么对于题目中的字符串s，我们可以根据pair将其划分为若干个子序列，每个自序列都是一个好字符串

步骤

1.利用并查集将字符串s分为若干个好字符串

2.创建一个哈希表，依次遍历字符串，设当前下标为u，其代表元素为v,则给map[v].push_back(v);

3.因为我们是按照顺序插入的，令a=map[v],对a进行排序，然后对应的将a[i]插入到map[v]中

代码

class Solution {
public:
    int query(vector<int>&parent,int index){
        if(parent[index]!=index){
            parent[index]=query(parent,parent[index]);
        }
        return parent[index];
    }
    void merge(vector<int>&parent,vector<int>&rank,int a,int b){
        int fa=query(parent,a);
        int fb=query(parent,b);
        if(fa==fb){
            return;
        }
        if(rank[fa]<=rank[fb]){
            parent[fa]=fb;
        }else{
            parent[fb]=fa;
        }
        if(rank[fa]==rank[fb]){
            rank[fb]++;
        }
        return;
    }
    string smallestStringWithSwaps(string s, vector<vector<int>>& pairs) {
		int n=s.size();
        vector<int> parent(n);
        vector<int> rank(n);
        for(int i=0;i<n;i++){
            parent[i]=i;
            rank[i]=1;
        }
        int m=pairs.size();
        for(int i=0;i<m;i++){
            merge(parent,rank,pairs[i][0],pairs[i][1]);
        }
        map<int,vector<int>> diff;
        for(int i=0;i<n;i++){
            int u=query(parent,i);
            diff[u].push_back(i);
        }
        vector<char> r(n);
        for(auto &[k,v] : diff){
            vector<int> c=v;
            sort(v.begin(),v.end(),[&](auto a,auto b){
                return s[a]<s[b];
            });
            for(int j=0;j<c.size();j++){
                r[c[j]]=s[v[j]];
            }
        }
        string res;
        for(auto& c:r){
            res+=c;
        }
        return res;
    }
};

细节

因为我们开始时直接按顺序给哈希表中插入数据的，所以中后将v数组排序之后就可以直接按照c数组进行赋值了

4.连接所有点的最小费用

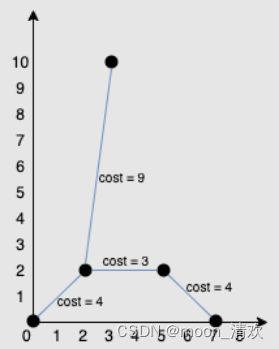
给你一个points 数组，表示 2D 平面上的一些点，其中 points[i] = [xi, yi] 。

连接点 [xi, yi] 和点 [xj, yj] 的费用为它们之间的 曼哈顿距离 ：|xi - xj| + |yi - yj| ，其中 |val| 表示 val 的绝对值。

返回将所有点连接的最小总费用

思路

这个题是哈夫曼编码的变形，所以我们可以沿用哈夫曼编码的思想去做，将所有边按大小排序，先从小边开始连接，当出现环时，不连接

另外，连接n个点在无环的情况下会有n-1条边，可以用这个作为一个判断条件

代码

class Solution {
public:
    int query(vector<int>&parent,int index){
        if(parent[index]!=index){
            parent[index]=query(parent,parent[index]);
        }
        return parent[index];
    }
    void merge(vector<int>&parent,vector<int>&rank,int a,int b){
        int fa=query(parent,a);
        int fb=query(parent,b);
        if(fa==fb){
            return;
        }
        if(rank[fa]<=rank[fb]){
            parent[fa]=fb;
        }else{
            parent[fb]=fa;
        }
        if(rank[fa]==rank[fb]){
            rank[fb]++;
        }
        return;
    }
    int minCostConnectPoints(vector<vector<int>>& points) {
		vector<tuple<int,int,int>> edge;
        int n=points.size();
        vector<int> parent(n);
        vector<int> rank(n);
        for(int i=0;i<n;i++){
            parent[i]=i;
            rank[i]=1;
        }
        for(int i=0;i<n;i++){
            for(int j=i+1;j<n;j++){
                edge.emplace_back(i,j,abs(points[i][0]-points[j][0])+abs(points[i][1]-points[j][1]));
            }
        }
        sort(edge.begin(),edge.end(),[&](const auto a,const auto b){
            auto &&[x1,y1,v1]=a;
            auto &&[x2,y2,v2]=b;
            return v1<v2;
        });
        int m=edge.size();
        int sum=0;
        int ans=0;
        for(const auto [x,y,v]:edge){
            if(sum==n-1){
                break;
            }
            if(query(parent,x)==query(parent,y)){
                continue;
            }
            merge(parent,rank,x,y);
            ans+=v;
        }
        return ans;
                                  
                                  
    }
};

细节

对三元数组vector>的运用

5.除法求值

这道题非常特殊，涉及到了并查集的特殊算法：$带权并查集$

我们设一个元素x的数值为v[x]，设x和y处于相同的集和，有公共的元素f,且v[x]/v[f]=a,v[y]/v[f]=b

则v[x]/v[y]=a/b;

所以我们可以看出，这里的a和b相当重要，我们记录v[x]和v[f]的比值为x的权值

记录w[x]=v[x]/v[f]

由于我们每次进行合并操作的时候，可能会对节点的指向有所改变

所以不仅要维护parent数组，还有要维护w数组

每次都令w[x]=v[x]/x[f]

查询的细节操作

如果f[x]!=x

另g=f[f[x]]

则w[x]=v[x]/x[g]=v[x]/v[f] * (v[f]/v[g])=w[x] * w[f[x]]

当我们合并两个节点x,y时

先找到x,y的父亲fx,fy

f[f[x]]=f[y]

w[f[x]]=v[f[x]]/x[f[y]]=(v[x]/w[x])/(v[y]/w[y])=(v[x]/v[y])*(w[y]/w[x])

v[x]/v[y]是会给出来的

class Solution {
public:
    int find(vector<int>&parent,vector<double>&weight,int index){
        if(index!=parent[index]){
            int origin=parent[index];
            parent[index]=find(parent,weight,parent[index]);
            weight[index]*=weight[origin];
        }
        return parent[index];
    }
    void link(vector<int>& parent,vector<double>&weight,int a,int b,double value){
        int roota=find(parent,weight,a);
        int rootb=find(parent,weight,b);
        if(roota==rootb){
            return;
        }
        parent[roota]=rootb;
        weight[roota]=weight[b]*value/weight[a];
    }
    double f(vector<int>& parent,vector<double>&weight,int a,int b){
        int roota=find(parent,weight,a);
        int rootb=find(parent,weight,b);
        if(roota!=rootb){
            return -1;
        }
            return weight[a]/weight[b];
        
    }
    vector<double> calcEquation(vector<vector<string>>& equations, vector<double>& values, vector<vector<string>>& queries) {
        int n=equations.size();
        vector<int> parent(2*n);
        vector<double> weight(2*n);
        for(int i=0;i<2*n;i++){
            parent[i]=i;
            weight[i]=1.0;
        }
        unordered_map<string,int> map;
        int idx=0;
        for(int i=0;i<n;i++){
            if(map.find(equations[i][0])==map.end()){
                map[equations[i][0]]=idx;
                idx++;
            }
            if(map.find(equations[i][1])==map.end()){
                map[equations[i][1]]=idx;
                idx++;
            }
            link(parent,weight,map[equations[i][0]],map[equations[i][1]],values[i]);
        }
        vector<double> res(queries.size(),-1);
        for(int i=0;i<queries.size();i++){
            string a=queries[i][0];
            string b=queries[i][1];
            if(map.find(a)!=map.end()&&map.find(b)!=map.end()){
                int idx1=map[a];
                int idx2=map[b];
                res[i]=f(parent,weight,idx1,idx2);
            }
        }
        return res;
    };
};