前言
变形储备
分子二次型且分母一次型的分式函数的变形,如\(h(x)=\cfrac{x^2-4x+5}{x-2}\),常用配凑法+分离常数法,或配凑法+分式裂项法,或换元法,
如[配凑法]\(h(x)=\cfrac{x^2-4x+5}{x-2}=\cfrac{(x-2)^2+1}{x-2}=(x-2)+\cfrac{1}{x-2}\),
或[换元法]令\(x-2=t\),则\(x=t+2\),故\(h(x)=\cfrac{(t+2)^2-4(t+2)+5}{t}=\cfrac{t^2+1}{t}=t+\cfrac{1}{t}\)
即\(h(x)=t+\cfrac{1}{t}=(x-2)+\cfrac{1}{x-2}\)
分子一次型且分母二次型的分式型函数的变形,如\(n(x)=\cfrac{x+1}{x^2+3x+3}\);常用取倒数法,或换元法,或配凑同除法
如\(n(x)=\cfrac{x+1}{(x+1)^2+(x+1)+1}=\cfrac{1}{(x+1)+\cfrac{1}{x+1}+1}\)
如\(g(t)=\cfrac{t}{t^2+9}=\cfrac{1}{t+\frac{9}{t}}\);
如\(h(t)=\cfrac{t+2}{t^2}=\cfrac{1}{t}+2(\cfrac{1}{t})^2=2m^2+m\);
组合使用
\(|OP|^2=\cfrac{(m^2+1)(m^2+16)}{(m^2+4)^2}\),令\(m^2+4=\lambda>4\),
则\(|OP|^2=\cfrac{(\lambda-3)(\lambda+12)}{\lambda^2}=-\cfrac{36}{\lambda^2}+\cfrac{9}{\lambda}+1\)
\(=-36(\cfrac{1}{\lambda}-\cfrac{1}{8})^2+\cfrac{25}{16}\leq \cfrac{25}{16}\).
例说运算
圆锥曲线中的范围最值问题的运算往往少不了以下的过程。
将直线\(y=kx+2\)代入圆锥曲线\(\cfrac{x^2}{4}+\cfrac{y^2}{3}=1\)的代入运算过程,可以如下简化:
先将圆锥曲线整理为\(3x^2+4y^2-12=0\),然后这样在演草纸上书写,注意对齐书写,一次运算过
\(\left\{\begin{array}{l}{3x^2}\\{4(k^2x^2+4kx+4)}\\{\hspace{6em}-12}\end{array}\right.\)
一次就可以整理为\((4k^2+3)x^2+16kx+4=0\);
思考策略
- 圆锥曲线上的点到定点的距离的最值问题
圆锥曲线上的点到定点的距离的最值问题,常用两点间的距离公式转化为区间上的二次函数的最值问题求解,有时也用圆锥曲线的参数方程,化为三角函数的最值问题求解,或用三角形的两边之和(或差)与第三边的不等关系求解;
- 圆锥曲线上的点到定直线的距离的最值问题
圆锥曲线上的点到定直线的距离的最值问题,常常采用平行切线法求解;
- 点在圆锥曲线上求目标函数的范围问题
点在圆锥曲线上(非线性约束条件)的条件下,求相关式子(目标函数)的取值范围问题,常用参数方程代入转化为三角函数的最值问题,或根据平面几何知识或引入一个参数(有几何意义)化为函数进行处理;
- 由直线和圆锥曲线位置关系求范围问题
由直线(系)和圆锥曲线(系)的位置关系,求直线或圆锥曲线中的某个参数(系数)的范围问题,常把所求参数作为函数,另一个元作为自变量,按照函数的值域方法求解;
思路点拨
最值问题
圆锥曲线中的最值问题类型较多,解法灵活多变,但总体上主要有两种方法:一是利用几何方法,即通过利用圆锥曲线的定义、几何性质以及平面几何中的定理、性质等进行求解;二是利用代数方法,即把需要求解最值的几何量或者代数式表示为某个(些)参数的函数(解析式),然后利用函数方法、不等式方法等进行求解。
在利用代数法解决最值或者范围问题时常从以下五个方面考虑:
①利用判别式来构造不等关系,从而确定参数的取值范围;
②利用已知参数的范围,求新参数的范围,解决这类问题的核心时在两个参数之间建立等量关系;
③利用隐含或已知的不等关系建立不等式,从而求出参数的取值范围;
④利用基本不等式求出参数的取值范围;
⑤利用函数的值域的求法,确定参数的取值范围。
范围问题
求范围问题的关键是建立求解关于某个变量的目标函数,通过求这个函数的值域问题确定目标的范围。在建立函数的过程中要根据题目的其他已知条件,把需要的量都用我们选用的变量表示,有时为了运算的方便,在建立关系的过程中也可以采用多个变量,只要在最后结果中将多变量归结为单变量即可,同时要特别注意变量的取值范围。
证明问题
圆锥曲线中的证明问题多涉及证明定值,证明点在定直线上等,有时也涉及一些否定性命题,证明方法一般采用直接法或反证法。证明定值时,一开始往往会含有参数,但是到最后的结果中,一定会将参数消去,结果中不含有未知数,故其为定值;证明点\((x_0,y_0)\)在直线上,则点的坐标一定满足直线方程或者直线方程一定能写成\(y-y_0=k(x-x_0)\)的形式。
典例剖析
例1【2019年陕西省告诉教学质量检测卷Ⅱ第20题】已知椭圆\(C:\cfrac{x^2}{a^2}+\cfrac{y^2}{b^2}=1(a>b>0)\)的左焦点为\(F\),离心率为\(\frac{\sqrt{2}}{2}\),短轴的两个端点分别为\(A\)、\(B\),\(S_{\triangle ABF}=1\)。
(1).求椭圆\(C\)的标准方程;
分析:示意图如图所示,由于\(S_{\triangle ABF}=1\),即\(\cfrac{1}{2}\cdot c\cdot 2b=1\),则\(bc=1\);
又由于\(e=\cfrac{c}{a}=\cfrac{\sqrt{2}}{2}\),则\(a=2k(k>0)\),\(c=\sqrt{2}k\),则\(b^2=a^2-c^2=2k^2\),\(b=\sqrt{2}k\),
由\(bc=1=2k^2\),解得\(k=\cfrac{\sqrt{2}}{2}\),故\(a=\sqrt{2}\),\(b=1\),
所以椭圆\(C\)的标准方程为\(\cfrac{x^2}{2}+y^2=1\);
(2).过点\(D(2,0)\)的直线\(l\)与椭圆\(C\)交于不同的两点\(M\),\(N\)(\(M\)在\(D\),\(N\)之间),求\(\frac{S_{\triangle ODM}}{S_{\triangle ODN}}\)(\(O\)为坐标原点)的取值范围;
分析:设\(M(x_1,y_1)\),\(N(x_2,y_2)\),
由于直线恒过点\(D(2,0)\),故可设直线\(l\)的方程为\(x=my+2\),
与椭圆方程\(\cfrac{x^2}{2}+y^2=1\)联立,
消掉\(x\)得到,\((m^2+2)y^2+4my+2=0\),
由\(\Delta=8m^2-16>0\),解得\(m^2>2\),
又由韦达定理得到,\(y_1+y_2=-\cfrac{4m}{m^2+2}\),\(y_1y_2=\cfrac{2}{m^2+2}\);
令\(\frac{S_{\triangle ODM}}{S_{\triangle ODN}}=\cfrac{|y_1|}{|y_2|}=t\)(则由于\(|y_1|<|y_2|\),则\(0
又由于\(\cfrac{(y_1+y_2)^2}{y_1y_2}=\cfrac{y_1^2+y_2^2+2y_1y_2}{y_1y_2}=\cfrac{y_1}{y_2}+\cfrac{y_2}{y_1}+2=t+\cfrac{1}{t}+2\);
且\(\cfrac{(y_1+y_2)^2}{y_1y_2}=\cfrac{8m^2}{m^2+2}=\cfrac{8}{1+\frac{2}{m^2}}\);
由于\(m^2>2\),则得到\(4<\cfrac{8}{1+\frac{2}{m^2}}<8\),故得到\(4
结合\(0
所以\(\frac{S_{\triangle ODM}}{S_{\triangle ODN}}\)的取值范围为\((3-2\sqrt{2},1)\);
名师点评:本题考查椭圆的标准方程、直线与椭圆的位置关系;考查函数与方程、转化与划归思想;考查数学运算、逻辑推理等核心素养。
例2【2019年高考数学试卷理科新课标Ⅱ第21题】已知点\(A(-2,0)\),\(B(-2,0)\),动点\(M(x,y)\)满足直线\(AM\)与\(BM\)的斜率之积为\(-\cfrac{1}{2}\),记\(M\)的轨迹为曲线\(C\)。
(1).求\(C\)的方程,并说明\(C\)是什么曲线;
分析:本题目可以用直接法得到曲线的方程,难点是要注意到不是恒等变形,需要添加条件。
解析:由于\(k_{AM}=\cfrac{y}{x+2}\),\(k_{BM}=\cfrac{y}{x-2}\),由题可知,\(k_{AM}\cdot k_{BM}=-\cfrac{1}{2}\),
即\(\cfrac{y}{x+2}\cdot \cfrac{y}{x-2}=-\cfrac{1}{2}\),化简得到\(x^2+2y^2=4\),
再整理为\(\cfrac{x^2}{4}+\cfrac{y^2}{2}=1\),
[此时,务必要注意,我们是将分式形式转化为整式形式,这一过程有去分母的变形,一定会扩大字母的取值范围,故需要添加条件才能保证变形前后是恒等变形,以此题为例,由于有分母,故需要\(|x|\neq 2\),或者对应到\(y\)值加以限制也是可以的,比如\(y\neq 0\)],
即曲线\(C\)的方程为\(\cfrac{x^2}{4}+\cfrac{y^2}{2}=1(|x|\neq 2)\),或者\(\cfrac{x^2}{4}+\cfrac{y^2}{2}=1(y\neq 0)\),所以\(C\)为中心在坐标原点,焦点在\(x\)轴上的椭圆,且不含左右顶点。
(2).过坐标原点的直线交\(C\)于\(P\)、\(Q\)两点,点\(P\)在第一象限,\(PE\perp x\)轴,垂足为\(E\),连结\(QE\)并延长交\(C\)于点\(G\),
①证明:\(\triangle PQG\)是直角三角形;②求\(\triangle PQG\)面积的最大值;
①证明:设\(P(x_0,y_0)\),则\(Q(-x_0,-y_0)\),\(E(x_0,0)\),\(G(x_G,y_G)\),
则直线\(QE\)的方程为:\(y=\cfrac{y_0}{2x_0}(x-x_0)\),与\(\cfrac{x^2}{4}+\cfrac{y^2}{2}=1\)联立,消去\(y\),
得到\((2x_0^2+y_0^2)x^2-2x_0y_0^2x+x_0^2y_0^2-8x_0^2=0\),\(-x_0\),\(x_G\)为方程的两个根,
则由韦达定理得到\(-x_0x_G=\cfrac{x_0^2y_0^2-8x_0^2}{2x_0^2+y_0^2}\),则\(x_G=\cfrac{(8-y_0^2)x_0}{2x_0^2+y_0^2}\)
则\(y_G=\cfrac{y_0}{2x_0}(x_G-x_0)=\cfrac{y_0(4-x_0^2-y_0^2)}{2x_0^2+y_0^2}\)
所以\(k_{PG}=\cfrac{y_G-y_0}{x_G-x_0}=\cfrac{\frac{y_0(4-x_0^2-y_0^2)}{2x_0^2+y_0^2} -y_0}{\frac{(8-y_0^2)x_0}{2x_0^2+y_0^2} -x_0}\)
\(=\cfrac{4y_0-y_0x_0^2-y_0^3-2y_0x_0^2-y_0^3}{8x_0-x_0y_0^2-2x_0^3-x_0y_0^2}\)
\(=\cfrac{y_0(4-3x_0^2-2y_0^2)}{2x_0(4-y_0^2-x_0^2)}\)
把\(x_0^2+2y_0^2=4\)代入上式,
得到\(k_{PG}=\cfrac{y_0(4-3x_0^2-4+x_0^2)}{2x_0(4-y_0^2-4+2y_0^2)}=\cfrac{-y_0\times 2x_0^2}{2x_0y_0^2}=-\cfrac{x_0}{y_0}\),
所以\(k_{PQ}\times K_{PG}=\cfrac{y_0}{x_0}\times (-\cfrac{x_0}{y_0})=-1\),
故\(PQ\perp PG\),故\(\triangle PQG\)为直角三角形。
②解:\(S_{\triangle PQG}=\cfrac{1}{2}|PE|\times (x_G-x_Q)=\cfrac{1}{2}y_0(x_G+x_0)\)
\(=\cfrac{1}{2}y_0[\frac{(8-y_0^2)x_0}{2x_0^2+y_0^2}+x_0]\)
\(=\cfrac{1}{2}y_0x_0\times \cfrac{8-y_0^2+2x_0^2+y_0^2}{2x_0^2+y_0^2}\)
\(=\cfrac{y_0x_0(4+x_0^2)}{2x_0^2+y_0^2}=\cfrac{y_0x_0(x_0^2+2y_0^2+x_0^2)}{2x_0^2+y_0^2}\)
\(=\cfrac{2y_0x_0(x_0^2+y_0^2)}{2x_0^2+y_0^2}\)
\(=\cfrac{8y_0x_0(x_0^2+y_0^2)}{(2x_0^2+y_0^2)(x_0^2+2y_0^2)}\),1
\(=\cfrac{8(y_0x_0^3+x_0y_0^3)}{2x_0^4+2y_0^4+5x_0^2y_0^2}\)
\(\xlongequal[化简整理得到]{给分子分母同除以x_0^2y_0^2}\) \(\cfrac{8(\frac{x_0}{y_0}+\frac{y_0}{x_0})}{2(\frac{x_0}{y_0}+\frac{y_0}{x_0})^2+1}\)
令\(t=\frac{x_0}{y_0}+\frac{y_0}{x_0}\),则\(t\geqslant 2\),
则\(S_{\triangle PQG}=\cfrac{8t}{2t^2+1}=\cfrac{8}{2t+\frac{1}{t}}\)
利用对勾函数\(f(t)=2t+\cfrac{1}{t}\)在\([2,+\infty)\)上的单调性可知,
\(f(t)\geqslant 4+\cfrac{1}{2}=\cfrac{9}{2}\)(当\(t=2\)时取到等号)
所以\(S_{\triangle PQG}\leqslant \cfrac{8}{\frac{9}{2}}=\cfrac{16}{9}\)
故\(\triangle PQG\)面积的最大值为\(\cfrac{16}{9}\).
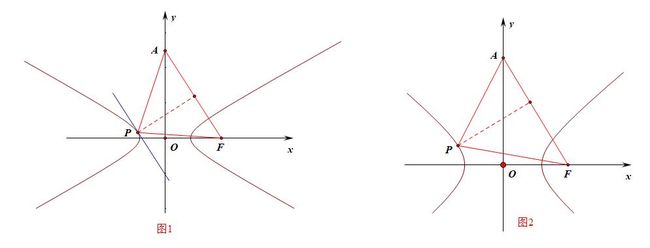
例3【2016陕西省二检理科第16题】已知F是双曲线C:\(x^2-\cfrac{y^2}{8}=1\)的右焦点,若\(P\)是\(C\)的左支上的一点,\(A(0,6\sqrt{6})\)是\(y\)轴上的一点,求\(\Delta APF\)面积的最小值。
分析:求\(\Delta APF\)面积的最小值,其中边AF长度固定,故只需要求边AF上的高线的最小值即可。
法1、平行线法,如图1所示,容易知道点\(F(3,0)\),故直线\(AF:2\sqrt{6}x+y-6\sqrt{6}=0\),
设\(l\)和直线AF平行且和双曲线的左支相切与点P,故直线\(l:2\sqrt{6}x+y+m=0\),
联立\(2\sqrt{6}x+y+m=0\)和\(x^2-\cfrac{y^2}{8}=1\),消\(y\)得到\(16x^2+4\sqrt{6}mx+m^2+8=0\),
由于相切得到\(\Delta =96m^2-4\times16(m^2+8)=0\),解得\(m=\pm 4\),结合图像将\(m=-4舍弃\),
即直线\(l:2\sqrt{6}x+y+4=0\),故三角形的高的最小值即两条平行线的间距,
故AF边上的高\(h=\cfrac{|4-(-6\sqrt{6})|}{\sqrt{(2\sqrt{6})^2+1}}=\cfrac{6\sqrt{6}+4}{5}\),
故\(S_{min}=\cfrac{1}{2}\times|AF|\times \cfrac{6\sqrt{6}+4}{5}=\cfrac{1}{2}\times15\times \cfrac{6\sqrt{6}+4}{5}=9\sqrt{6}+6\)。
法2、函数法,如图2所示,由题目可知双曲线的左支对应的函数为\(y=f(x)=\pm\sqrt{8x^2-8}(x<0)\),
设点\(P(x_0,y_0)\),则\(f'(x)=\pm\cfrac{1}{2\sqrt{8x^2-8}}\cdot 16x=\pm\cfrac{8x}{\sqrt{8x^2-8}}\),
结合图像可知\(f'(x)<0\),故取\(f'(x)=\cfrac{8x}{\sqrt{8x^2-8}}(x<0)\),当\(f'(x)=k_{AF}=-2\sqrt{6}\)时,
AF边上的高线最小(可结合平行线法理解),故\(\cfrac{8x_0}{\sqrt{8x_0^2-8}}=-2\sqrt{6}\),
解得\(x_0=-\cfrac{\sqrt{6}}{2}\),代入得到\(y=2\),即切点\(P(-\cfrac{\sqrt{6}}{2},2)\),
故高\(h=\cfrac{|2\sqrt{6}\cdot(-\cfrac{\sqrt{6}}{2})+2-6\sqrt{6}|}{5}=\cfrac{6\sqrt{6}+4}{5}\),
故\(S_{min}=\cfrac{1}{2}\times|AF|\times \cfrac{6\sqrt{6}+4}{5}=\cfrac{1}{2}\times15\times \cfrac{6\sqrt{6}+4}{5}=9\sqrt{6}+6\)。
法3、参数方程法,不要求学生掌握。由于双曲线为\(x^2-\cfrac{y^2}{8}=1\),
故其参数方程为\(\begin{cases}x=\cfrac{1}{cos\theta}\\y=2\sqrt{2}tan\theta\end{cases}(\theta为参数)\),
故\(h=\cfrac{|\cfrac{2\sqrt{6}}{cos\theta}+2\sqrt{2}tan\theta-6\sqrt{6}|}{5}=\cfrac{|\cfrac{2\sqrt{6}}{cos\theta}+\cfrac{2\sqrt{2}sin\theta}{cos\theta}-6\sqrt{6}|}{5}\),
以下难点转化为求\(\cfrac{2\sqrt{6}}{cos\theta}+\cfrac{2\sqrt{2}sin\theta}{cos\theta}\)的值。
令\(m=\cfrac{2\sqrt{6}}{cos\theta}+\cfrac{2\sqrt{2}sin\theta}{cos\theta}\),
则有\(2\sqrt{6}+2\sqrt{2}sin\theta=mcos\theta\),故\(\sqrt{m^2+8}cos\theta=2\sqrt{6}\),
即\(cos\theta=\cfrac{2\sqrt{6}}{\sqrt{m^2+8}}\),故\(|cos\theta|=|\cfrac{2\sqrt{6}}{\sqrt{m^2+8}}|\leq 1\),
解得\(m\ge 4\)或者\(m\leq -4\),由于参数\(\theta\in(0,\pi)\),且点P在左支,
故\(\theta\in(\cfrac{\pi}{2},\pi)\),故\(m<0\),故当\(m=-4\)时\(d\)有最小值,
此时\(d_{min}=\cfrac{|-4-6\sqrt{6}|}{5}=\cfrac{4+6\sqrt{6}}{5}\),
故\(S_{min}=\cfrac{1}{2}\times|AF|\times \cfrac{6\sqrt{6}+4}{5}=\cfrac{1}{2}\times15\times \cfrac{6\sqrt{6}+4}{5}=9\sqrt{6}+6\)。
例4【2019届高三理科数学二轮用题】已知\(F_1\),\(F_2\)分别是双曲线\(C:\cfrac{x^2}{a^2}-\cfrac{y^2}{b^2}=1\) \((a>0,b>0)\)的左右焦点,以\(F_2\)为圆心做一个圆,使该圆过线段\(OF_2\)的中点,若该圆与双曲线的两条渐近线有公共点,则双曲线\(C\)的离心率的取值范围是___________。
分析:如下图所示,可知圆\(F_2\)的圆心为\(F_2(c,0)\),半径为\(r=\cfrac{c}{2}\),由于圆和双曲线都关于坐标轴对称,故只需要保证圆和一条渐近线\(y=\cfrac{b}{a}x\)有公共点即可,
![]()
此时可以使用联立直线方程和双曲线的方程,使用\(\Delta \ge 0\)的思路,也可以利用圆心到直线的距离小于半径的思路,很明显第二个思路的运算量要小一些。
此时圆心为\(F_2(c,0)\),半径为\(r=\cfrac{c}{2}\),直线为\(bx-ay=0\),故\(d=\cfrac{|bc-a\times 0|}{\sqrt{a^2+b^2}}\leq \cfrac{c}{2}\),
化简整理得到,\(2b\leq c\),即\(4b^2\leq c^2\),则\(4c^2-4a^2\leq c^2\),整理为\(\cfrac{c^2}{a^2}\leq \cfrac{4}{3}\),故\(e\leq \cfrac{2\sqrt{3}}{3}\),又双曲线的\(e>1\),故\(e\in (1,\cfrac{2\sqrt{3}}{3}]\).
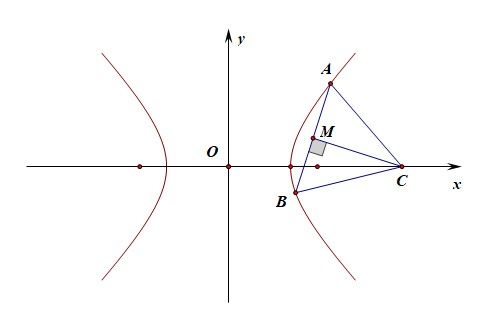
例5【2019高三理科数学启动卷,2019陕西省二检试卷第16题】已知等腰\(\triangle ABC\)的底边端点\(A\),\(B\)在双曲线\(\cfrac{x^2}{6}-\cfrac{y^2}{3}=1\)的右支上,顶点\(C\)在\(x\)轴上,且\(AB\)不垂直于\(x\)轴,则顶点\(C\)的横坐标\(t\)的取值范围是__________。
分析:设\(A(x_1,y_1)\),\(B(x_2,y_2)\),弦\(AB\)的垂直平分线交\(x\)轴于点\(C(t,0)\),
\(AB\)的中点为\(M(x_0,y_0)\),则\(x_0>\sqrt{6}\),
由题意有\(\cfrac{x_1^2}{6}-\cfrac{y_1^2}{3}=1\)①,\(\cfrac{x_2^2}{6}-\cfrac{y_2^2}{3}=1\)②,两式相减得到,
\((x_1+x_2)(x_1-x_2)-2(y_1+y_2)(y_1-y_2)=0\),于是有\(x_0(x_1-x_2)-2y_0(y_1-y_2)=0\),
即\(k_{AB}=\cfrac{y_2-y_1}{x_2-x_1}=\cfrac{x_0}{2y_0}\),又\(k_{MC}=\cfrac{y_0}{x_0-t}\),由\(k_{AB}\cdot k_{MC}=-1\)得到,
\(\cfrac{y_0}{x_0-t}\cdot \cfrac{x_0}{2y_0}=-1\),即\(x_0+2(x_0-t)=0\),则\(t=\cfrac{3x_0}{2}>\cfrac{3\sqrt{6}}{2}\)。
故\(t\in (\cfrac{3\sqrt{6}}{2},+\infty)\)。
例6已知抛物线\(C:y^2=4x\)的焦点为\(F\),过点\(M(4,0)\)的直线与抛物线\(C\)交于\(A\),\(B\)两点,则\(\triangle ABF\)的面积的最小值为【】
法1:做出如下的示意图,设直线\(AB\)的斜率为\(k\),不妨只考虑\(k>0\),则\(AB:y=k(x-4)\),即\(kx-y-4k=0\);
将直线和抛物线方程联立,消去\(x\)得到,\(ky^2-4y-16k=0\),则\(y_1+y_2=-\cfrac{-4}{k}=\cfrac{4}{k}\),\(y_1y_2=-16\),
则\(|AB|=\sqrt{1+\cfrac{1}{k^2}}|y_1-y_2|=\sqrt{1+\cfrac{1}{k^2}}\sqrt{(y_1+y_2)^2-4y_1y_2}\)
\(=\sqrt{1+\cfrac{1}{k^2}}\sqrt{(\cfrac{4}{k})^2-4\times (-16)}=\sqrt{\cfrac{k^2+1}{k^2}}\cdot 4\cdot \sqrt{\cfrac{4k^2+1}{k^2}}\)
\(=4\cdot \cfrac{\sqrt{k^2+1}\cdot \sqrt{4k^2+1}}{k^2}\),
又点\(F\)到直线\(AB\)的距离为\(d=h=\cfrac{|3k|}{\sqrt{k^2+1}}=\cfrac{3k}{\sqrt{k^2+1}}\),
则\(S_{\triangle ABF}=\cfrac{1}{2}\cdot 4\cdot \cfrac{\sqrt{k^2+1}\cdot \sqrt{4k^2+1}}{k^2}\cdot \cfrac{3k}{\sqrt{k^2+1}}\)
\(=6\times \cfrac{\sqrt{4k^2+1}}{k}=6\times \sqrt{4+\cfrac{1}{k^2}}\),
当\(k\rightarrow \infty\)时,所求面积有最小值,\(S_{min}=6\times 2=12\)。故选\(B\).
法2:仿上利用均值不等式可以说明,当\(AB\)和\(x\)轴垂直时,\(S_{\triangle ABF}\)有最小值;
\(S_{\triangle ABF}=\cfrac{1}{2}\cdot 3\cdot (|y_1|+|y_2|)\ge \cfrac{3}{2}\cdot 2\sqrt{|y_1y_2|}= \cfrac{3}{2}\cdot 2\cdot 4=12\),故选\(B\).
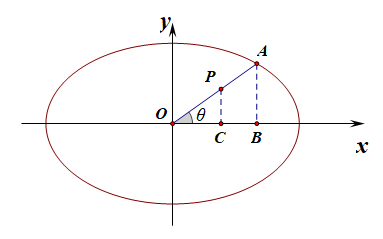
例7【均值不等式的使用】在平面直角坐标系\(xoy\)中,已知点\(A\)在椭圆\(\cfrac{x^2}{16}+\cfrac{y^2}{8}=1\)上,点\(P\)满足\(\overrightarrow{AP}=(\lambda-1)\overrightarrow{OA}(\lambda\in R)\),且\(\overrightarrow{OA}\cdot \overrightarrow{OP}=12\),求线段\(OP\)在\(x\)轴上的投影长度的最大值。
解析:由\(\overrightarrow{AP}=(\lambda-1)\overrightarrow{OA}\),即\(\overrightarrow{OP}-\overrightarrow{OA}=(\lambda-1)\overrightarrow{OA}\)
则有\(\overrightarrow{OP}=\lambda\overrightarrow{OA}\),故\(O、P、A\)三点共线,由\(\overrightarrow{OA}\cdot \overrightarrow{OP}=12\),得到\(|\overrightarrow{OA}|\cdot |\overrightarrow{OP}|=12\),
设OP与\(x\)轴的夹角为\(\theta\),点\(A(x,y)\),\(B\)为点\(A\)在\(x\)轴上的投影,由图可知,线段\(OP\)在\(x\)轴上的投影长度为\(||\overrightarrow{OP}|\cdot cos\theta|\)
则\(||\overrightarrow{OP}|\cdot cos\theta|=|\overrightarrow{OP}|\times \cfrac{|\overrightarrow{OB}|}{|\overrightarrow{OA}|}\)\(=\cfrac{12}{|\overrightarrow{OA}|}\times \cfrac{|\overrightarrow{OB}|}{|\overrightarrow{OA}|}\)
\(=12\cdot \cfrac{|\overrightarrow{OB}|}{|\overrightarrow{OA}|^2}\),又由于\(|\overrightarrow{OB}|=|x|\),\(|\overrightarrow{OA}|=\sqrt{x^2+y^2}\),
\(=12\times \cfrac{|x|}{x^2+y^2}\), 接下来施行变量集中,由于\(\cfrac{x^2}{16}+\cfrac{y^2}{8}=1\),得到\(y^2=8-\cfrac{x^2}{2}\),代入
\(=12\times \cfrac{|x|}{\cfrac{x^2}{2}+8}\),分子分母同除以\(|x|\)得到,
\(=12\times \cfrac{1}{\frac{|x|}{2}+\frac{8}{|x|}}\leq 12\times \cfrac{1}{4}=3\),
当且仅当\(|x|=4\)时等号成立,故线段\(OP\)在\(x\)轴上的投影长度的最大值为\(3\)。
例8已知椭圆\(C:\cfrac{x^2}{a^2}+\cfrac{y^2}{b^2}=1(a>b>0)\)的离心率为\(\cfrac{1}{2}\),以原点\(O\)为圆心,以短轴为直径的圆的面积为\(3\pi\)。
(1)求椭圆\(C\)的方程;
分析:由\(e=\cfrac{c}{a}=\cfrac{1}{2}\),则\(e^2=\cfrac{a^2-b^2}{a^2}=\cfrac{1}{4}\),即\(a^2=\cfrac{4}{3}b^2\),
又以短轴为直径的圆的面积为\(3\pi\),则\(3\pi=b^2\pi\),则\(b^2=3\),\(a^2=4\),
故椭圆的方程为\(\cfrac{x^2}{4}+\cfrac{y^2}{3}=1\).
(2)过点\(M(4,0)\)的直线与椭圆\(C\)相交于\(A\)、\(B\)两点,求\(\overrightarrow{OA}\cdot \overrightarrow{OB}\)的最小值;
分析:由题意可知,直线\(l\)的斜率存在,故设直线\(l\)的方程为\(y=k(x-4)\),
由\(\left\{\begin{array}{l}{y=k(x-4)}\\{\cfrac{x^2}{4}+\cfrac{y^2}{3}=1,}\end{array}\right.\) 得到\((4k^2+3)x^2-32k^2x+64k^2-12=0\),
由\(\Delta=(-32k^2)^2-4(4k^2+3)(64k^2-12)>0\),解得\(k^2<\cfrac{1}{4}\),
设\(A(x_1,y_1)\)、\(B(x_2,y_2)\),则由韦达定理可知,\(x_1+x_2=\cfrac{32k^2}{4k^2+3}\),\(x_1x_2=\cfrac{64k^2-12}{4k^2+3}\),
所以\(y_1y_2=k(x_1-4)\cdot k(x_2-4)=k^2x_1x_2-4k^2(x_1+x_2)+16k^2\),
则\(\overrightarrow{OA}\cdot \overrightarrow{OB}=x_1x_2+y_1y_2=(1+k^2)\cfrac{64k^2-12}{4k^2+3}-4k^2\cdot \cfrac{32k^2}{4k^2+3}+16k^2\)
\(=25-\cfrac{87}{4k^2+3}\),
由于\(0\leqslant k^2<\cfrac{1}{4}\),则\(-\cfrac{87}{3}\leqslant -\cfrac{87}{4k^2+3}<-\cfrac{87}{4}\),
即\(25-\cfrac{87}{3}\leqslant 25-\cfrac{87}{4k^2+3}<25-\cfrac{87}{4}\),
故\(\overrightarrow{OA}\cdot \overrightarrow{OB}\)的最小值为\(25-\cfrac{87}{3}=25-29=-4\).
例9【2019届高三理科数学三轮模拟试题】已知点\(A\)在离心率为\(\cfrac{\sqrt{2}}{2}\)的椭圆\(C:\cfrac{x^2}{a^2}+\cfrac{y^2}{b^2}=1(a>b>0)\)上,左、右焦点分别为\(F_1\),\(F_2\),\(\triangle AF_1F_2\)的内切圆的半径\(r=\sqrt{2}-1\),且\(S_{\triangle AF_1F_2}=1\),
(1)求椭圆\(C\)的方程;
分析:由三角形面积公式可知,\(S_{\triangle AF_1F_2}=\cfrac{1}{2}(|AF_1|+|AF_2|+|F_1F_2|)\cdot r=1\),
即\(\cfrac{1}{2}(2a+2c)(\sqrt{2}-1)=1\),化简得到\(a+c=\sqrt{2}+1\)①;
又\(\cfrac{c}{a}=\cfrac{\sqrt{2}}{2}\)②,两式联立,解得\(c=1\),\(a=\sqrt{2}\),则\(b^2=a^2-c^2=1\),
故椭圆\(C\)的方程为\(\cfrac{x^2}{2}+y^2=1\);
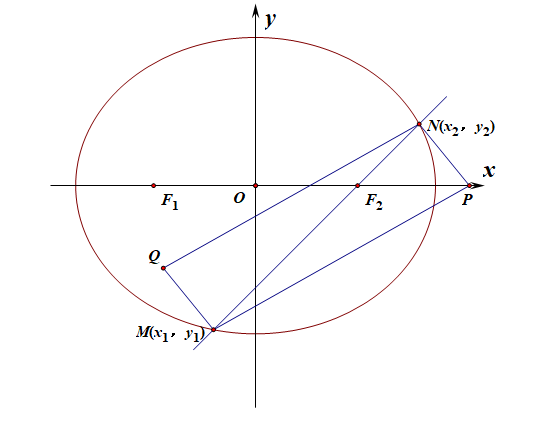
(2)过点\(F_2\)的直线\(l\)与椭圆\(C\)的交点为\(M\),\(N\),使得\(\overrightarrow{F_2M}=\lambda \overrightarrow{F_2N}\),其中\(\lambda\in [-2,-1]\),点\(P\)坐标为\((2,0)\),求平行四边形\(PMQN\)的对角线\(PQ\)长度的最小值;
分析:已知直线\(l\)斜率不为\(0\),设直线\(l\)为\(l:x=ky+1\),
由\(\left\{\begin{array}{l}{x=ky+1}\\{x^2+2y^2=2}\end{array}\right.\) 得到\((k^2+2)y^2+2ky-1=0\),
其中\(\Delta=4k^2-4(k^2+2)(-1)=8(k^2+1)>0\),设\(M(x_1,y_1)\),\(N(x_2,y_2)\),
则有\(y_1+y_2=\cfrac{-2k}{k^2+2}\),\(y_1y_2=\cfrac{-1}{k^2+2}\),
又由于\(\overrightarrow{F_2M}=\lambda \overrightarrow{F_2N}\),即\((x_1-1,y_1)=\lambda(x_2-1,y_2)\),则有\(y_1=\lambda y_2\),
即\(\left\{\begin{array}{l}{y_1+y_2=(\lambda+1)y_2=\cfrac{-2k}{k^2+2}①}\\{y_1y_2=\lambda y_2^2=\cfrac{-1}{k^2+2}②}\end{array}\right.\)
\(\cfrac{①^2}{②}\),得到\(\cfrac{(\lambda+1)^2}{\lambda}=\lambda+\cfrac{1}{\lambda}+2=\cfrac{-4k^2}{k^2+2}\);
由于\(\lambda\in [-2,-1]\),则\(\lambda+\cfrac{1}{\lambda}+2\in [-\cfrac{1}{2},0]\),
即\(-\cfrac{1}{2}\leqslant \cfrac{-4k^2}{k^2+2}\leqslant 0\),解得\(0\leqslant k^2\leqslant \cfrac{2}{7}\),
由\(\overrightarrow{PQ}=\overrightarrow{PM}+\overrightarrow{PN}=(x_1+x_2-4,y_1+y_2)\)\(=(\cfrac{-4(k^2+1)}{k^2+2},\cfrac{-2k}{k^2+2})\),
则\(|\overrightarrow{PQ}|^2=(\cfrac{-4(k^2+1)}{k^2+2})^2+(\cfrac{-2k}{k^2+2})^2\),
化简得到\(|\overrightarrow{PQ}|^2=\cfrac{8}{(k^2+2)^2}-\cfrac{28}{k^2+2}+16\),
令\(t=\cfrac{1}{k^2+2}\),则\(t\in [\cfrac{7}{16},\cfrac{1}{2}]\),
则\(|\overrightarrow{PQ}|^2=8t^2-28t+16\),对称轴为\(t=\cfrac{7}{4}\),
故当\(t=\cfrac{1}{2}\)时,\(|PQ|_{min}=2\);
由于\(x_0^2+2y_0^2=4\),故给分子乘以\(4\)得到\(8y_0x_0(x_0^2+y_0^2)\);给分母乘以\((x_0^2+2y_0^2)\),目的是为了在分子分母位置构造四次齐次式,便于下一步变量集中,为利用函数求解最值埋下伏笔;↩