LBP特征提取原理和python库代码
1局部二值模式
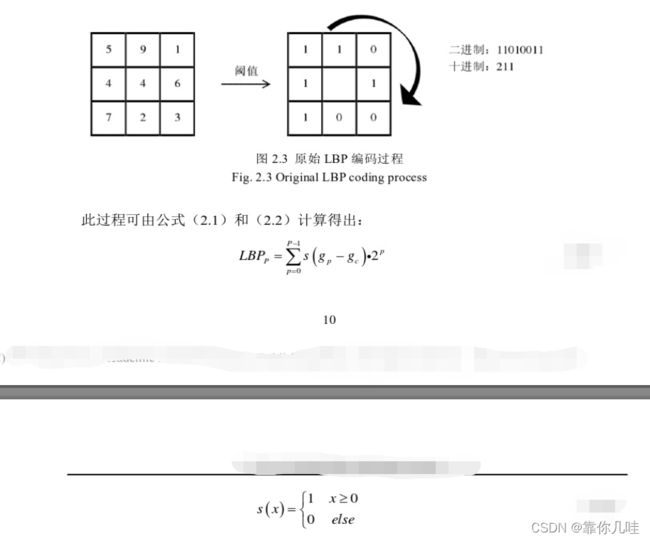
局部二值模式( Local binary pattern, LBP )图作为- - 种传统的表情提取特征的方法,有着不可替代的优势。在1994 年被Ojala等人首次提出并作出定义计算。他最大的特点就是当图像数据中的灰度值不易被影响而发生改变,同时,对图像数据进行转向操作而不影响表情特征的提取。该方法的过程共分三步,如图
1将图像中的某一一个像素点及其周围的8邻域像素点组合在一-起, 定义为一个3x3的窗口。
2以该像素点的灰度值也就是窗口中心点的灰度值作为阈值,与其周围8邻域像素点的灰度值依次进行比较,8邻域像素点灰度值中大于阙值的位置被置为1,小于阈值的位置被置为0。
3将经过(2)步骤得到的二进制数按照顺时针或者逆时针旋转的顺序排列起来(图中采用的是顺时针旋转的方式),将得到的结果从二进制转为十进制,此时得到的值就是该方法获取的特征值。
上述公式中,中心像素点的定位由LBP,来决定,P 确定的是相邻区域的像素点的数量,p提供的是相邻区域中排在P位置的像素点,g,确定了所有范围内在中心点周围其他区域的点的灰度值,g指的是所有范围内的中心点的灰度值,s(x)返回参数的正负号。
由上述的原始LBP算子计算过程不难看出,其并不具备旋转不变性的优点,换句话来说就是当图像发生旋转时,原始LBP算子也会发生改变。因为当图像发生旋转时,其纹理及形状却并不会因此发生变化,所以这是不被期望产生的情况。因此,为了解决原始LBP算子的这种局限性问题,Ojala及其团队又提出了改进的圆形LBP算子。圆形LBP算子结构如图2.4所示,相比于原始LBP算子来说,圆形LBP算子是将图像中某--像素点与其周围任意半径大小的圆形领域上的像素点组合在一-起定义的一个圆形领域。而在圆形邻域上会存在若千个像素点,因此,这里需要对圆形邻域进行采样,假设这个圆形邻域的半径大小为R,那么通过采样得到的邻域像素点数量为P,这,样就构成了该像素点的圆形LBP算子。之后将执行与原始LBP算子运算过程中的(2)(3)两个步骤相同的操作,即可得到由圆形LBP算子计算得出的LBP特征值。然而,在这里还有一- 个小问题,在对圆形邻域进行采样的过程中,并不是所有的采样坐标都一定会刚好落在像素点上,为了解决这一- 问题,将采用双线性插值来对这些没有落在像素上的领域值进行估计。
为了使这种圆形LBP算子具备旋转不变性的优点,Ojala 及其团队为其算法增加了-步与原始LBP算子计算过程不同的操作,即将圆形LBP算子进行-系列的旋转操作,这样就可以得到一系列不同的LBP特征值,将这些LBP特征值中的最小值作为该圆形LBP算子计算得出的LBP特征值。

图2.5展示的是LBP算子具有数据旋转但特征值能保持不变的特性,其中白色圆圈表示1,黑色圆圈表示0,因此通过计算原循环LBP算子表示的二进制数为1100001也就是十进制下的225。经过不断旋转后发现该圆形LBP算子拥有8种旋转角度,分别对应8种LBP特征值,经过比较,选取最小的LBP特征值15作为该圆形LBP算子的LBP特征值。
通过上述LBP算子的计算过程可以看出,原始LBP的特征模式每次有2的8次方种可能,而圆形LBP的特征模式每次有2"种可能,因此,不难发现,LBP 的特征模式数量随着不断地改进而呈现爆炸性的指数增长,而过多的特征值数量不仅会增加计算量,而且还可能影响计算效率。针对这一-问题, Ojala 及其团队又提出了一种既能够大幅减低特征维度又能够尽量保留图像信息的等价模式。这种模式的理论基础是他们研究发现,图像数据的二进制值一般只会发生两次变化,且二进制只包括0和1,因此根据这种特征定义了与LBP模式相似的模式类,且这种类中包含最多两次的数据改变。当实验采用了该模式后,原始LBP特征模式的数量降低为58种,圆形LBP特征模式的数量降低为Px(P-1)+2种。
LBP特征向量进行提取的步骤:
(1)首先将检测窗口划分为16×16的小区域(cell);
(2)对于每个cell中的一个像素,将相邻的8个像素的灰度值与其进行比较,若周围像素值大于中心像素值,则该像素点的位置被标记为1,否则为0。这样,3*3邻域内的8个点经比较可产生8位二进制数,即得到该窗口中心像素点的LBP值;
(3)然后计算每个cell的直方图,即每个数字(假定是十进制数LBP值)出现的频率;然后对该直方图进行归一化处理。
(4)最后将得到的每个cell的统计直方图进行连接成为一个特征向量,也就是整幅图的LBP纹理特征向量;
然后便可利用SVM或者其他机器学习算法进行分类了。参考一些博客中的代码实现效果如下:
#lbp是像素矩阵
lbp = feature.local_binary_pattern(img,n_point,radius,'default')
max_bins = int(lbp.max() + 1)#.max()取lbp中最大的数
#test_hist是某个灰度级的个数即y坐标。-是横坐标。
test_hist, _ = np.histogram(lbp, normed=True, bins=max_bins, range=(0,max_bins))
local_binary_pattern参数详解:
local_binary_pattern(image, P, R, method='default')
参数(调参)
image:(N,M)阵列灰度图像。(只能是灰度图)
P:int圆对称邻居设置点的数量(角度空间的量化)。
R:float圆的半径(操作员空间分辨率)。
method:{‘default’,‘ror’,‘uniform’,‘var’}确定模式的方法(调参使用)
'default':原始的局部二值模式,它是灰度但不是旋转不变的。
'ror':扩展灰度和旋转不变的默认实现。
'uniform':改进的旋转不变性和均匀的模式以及角度空间的更精细的量化,灰度和旋转不变。
'nri_uniform':非旋转不变的均匀图案变体,它只是灰度不变的R199。
'var':局部对比度的旋转不变方差度量,图像纹理是旋转但不是灰度不变的。
返回值:
输出:(N,M)阵列LBP图像
np.histogram()解释:
np.histogram()是一个生成直方图的函数
histogram(a,bins=10,range=None,weights=None,density=False);
a是待统计数据的数组;
bins指定统计的区间个数;
range是一个长度为2的元组,表示统计范围的最小值和最大值,默认值None,表示范围由数据的范围决定
weights为数组的每个元素指定了权值,histogram()会对区间中数组所对应的权值进行求和
density为True时,返回每个区间的概率密度;为False,返回每个区间中元素的个数
a = np.random.rand(100)
hist,bins = np.histogram(a,bins=5,range=(0,1))
print(hist)
print(bins)
[19 30 15 16 20]
[ 0. 0.3 0.4 0.6 0.9 1. ]