吴恩达机器学习--中文笔记--第四周
吴恩达机器学习
- 第四个星期
-
- 1.诱因和动机
-
- 1.1非线性假设函数
- 1.2神经元和大脑
- 2.神经网络
-
- 2.1模型表示(1)
- 2.2模型表示(2)
- 3.应用
-
- 3.1示例和直觉(1)
- 3.1示例和直觉(2)
- 3.3多类别分类
- 参考文献
本文是在学习吴恩达老师机器学习课程的基础上结合老师的ppt文献然后加上自身理解编写出来的,有些地方可能有遗漏或错误,欢迎大家批评指正。希望我们一起学习,一起进步!
第四个星期
1.诱因和动机
从这里开始进入神经网络的世界,所以首先介绍一下引入的原因作为一个承上启下的铺垫。
1.1非线性假设函数
当我们面对输入特征超多的情况下,再用前面所学的一般情况下的线性回归或逻辑回归的方法进行处理,还能行的通吗?
事实告诉我们,不行了,为啥呢,这里,我们假设有一千个输入特征,且多项式中全部是二次项( e . g . x i ∗ x j e.g.\;\;x_i*x_j e.g.xi∗xj),那么我们的参数会有多少呢?答:有 1000 ∗ 1000 / 2 = 500000 1000*1000/2=500000 1000∗1000/2=500000个。试想,每一次迭代都会进行500000次参数更新,这是多么大的计算压力,最重要的一点是,这么多的特征,难免会过拟合(overfitting)。
拿一张图片来做例子吧:
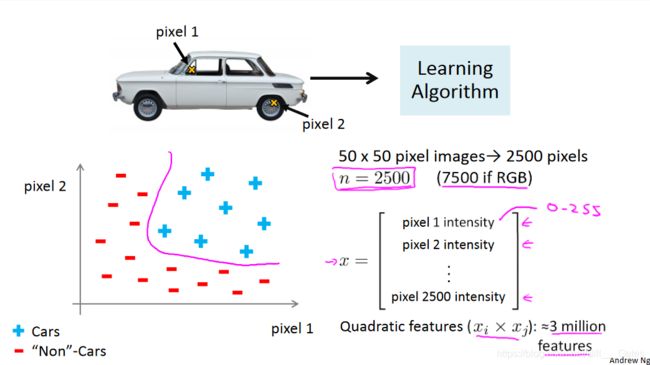
我们要判断一张图片是不是汽车(car),我们要把每一个像素(pixel)作为输入,假设这张图片是50*50像素的,那么它会有2500个像素点(灰度图像),且假设函数多项式全部为二次方特征( e . g . x i ∗ x j e.g. \;x_i*x_j e.g.xi∗xj),结果是参数量会达到恐怖的约3000000( 3 ∗ 1 0 6 3*10^6 3∗106)个,如果像素为7500个(RGB图像),结果是参数量会达到恐怖的约30000000( 3 ∗ 1 0 7 3*10^7 3∗107)个。
这样最终的结果就是,不仅计算量惊人,预测结果也很不好。
1.2神经元和大脑
神经网络的历史: 神经网络算法是一种试图模仿人大脑结构的算法,它在上世纪80年代和90年代早期被广泛使用,在90年代末期逐渐退热。近期复苏:多种应用的最新技术出现,被使用。
神经网络的可塑性: 人脑中的神经网络虽然分有很多的皮层区域,每个区域各司其职,但是,实际上,这都是长期训练的结果,实践表明,人的感知皮层经过训练可以具有“视觉功能”,听觉皮层经过训练,也可以具有“视觉功能”。
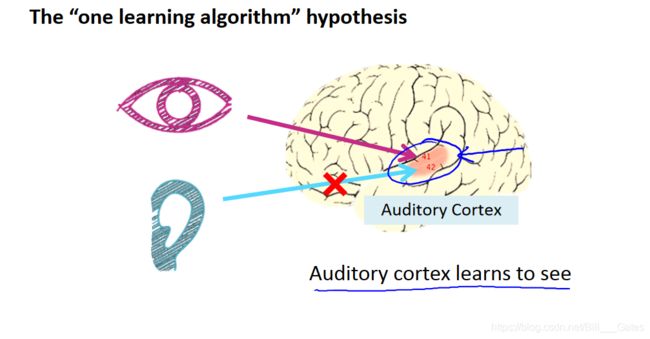
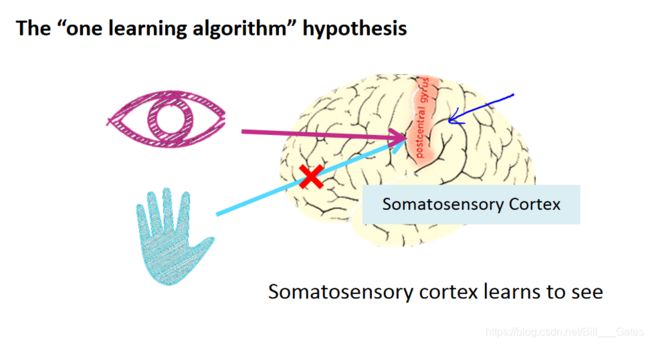
再比如下面这四个例子:
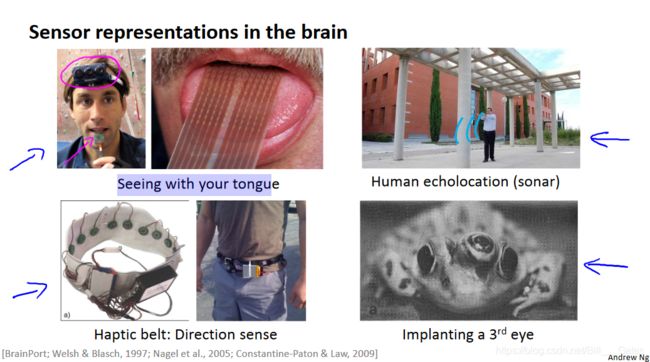
- 使用舌头连接摄像头,通过舌头感知刺激来实现感知视觉功能。
- 使用声呐系统,通过耳朵感知声呐刺激,进行人体回声定位,实现视觉功能。
- 触觉腰带,感知方向
- 在青蛙上植入第三只眼,并恢复视觉功能
2.神经网络
2.1模型表示(1)
神经网络模型运用了很多逻辑回归中的东西,在概念名称上做了一些变化,实际还是一个东西。神经网络中,我们将sigmoid function改为activation function(激活函数);把 θ \theta θtheta改为权重weight
简单来讲,神经网络模型可以这样表示:
[ x 0 , x 1 , x 2 ] − > [ h i d d e n l a y e r s ] − > h θ ( x ) [x_0,x_1,x_2]->[hidden\;layers]->h_\theta(x) [x0,x1,x2]−>[hiddenlayers]−>hθ(x)
所有输入节点为输入层(input layer),输出节点为输出层(output layer),那么其他层被叫做隐藏层(hidden layer)
通常情况下,我们用 a i ( j ) a_i^{(j)} ai(j)来表示隐藏层节点,它代表第j层的第个激活单元;用 Θ ( j ) \Theta^{(j)} Θ(j)来代表第j层至第j+1层的权重矩阵。
所以,假设我们只有一个隐藏层(3个节点),神经网络模型可以表示为:
[ x 0 , x 1 , x 2 , x 3 ] − > [ a 1 ( 2 ) , a 2 ( 2 ) , a 3 ( 2 ) ] − > h θ ( x ) [x_0,x_1,x_2,x_3]->[a_1^{(2)},a_2^{(2)},a_3^{(2)}]->h_\theta(x) [x0,x1,x2,x3]−>[a1(2),a2(2),a3(2)]−>hθ(x)
表示是表示完了,那层与层之间是如何连接的呢?首先给一张图,方便理解。
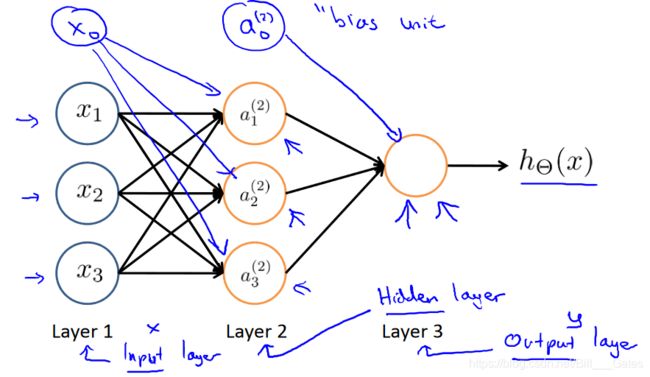
那么,我们可以对层与层的连接做数学解释了。通常情况下:
a 1 ( 2 ) = g ( Θ 10 ( 1 ) x 0 + Θ 11 ( 1 ) x 1 + Θ 12 ( 1 ) x 2 + Θ 13 ( 1 ) x 3 ) a_1^{(2)}=g(\Theta_{10}^{(1)}x_0+\Theta_{11}^{(1)}x_1+\Theta_{12}^{(1)}x_2+\Theta_{13}^{(1)}x_3) a1(2)=g(Θ10(1)x0+Θ11(1)x1+Θ12(1)x2+Θ13(1)x3)
a 2 ( 2 ) = g ( Θ 20 ( 1 ) x 0 + Θ 21 ( 1 ) x 1 + Θ 22 ( 1 ) x 2 + Θ 23 ( 1 ) x 3 ) a_2^{(2)}=g(\Theta_{20}^{(1)}x_0+\Theta_{21}^{(1)}x_1+\Theta_{22}^{(1)}x_2+\Theta_{23}^{(1)}x_3) a2(2)=g(Θ20(1)x0+Θ21(1)x1+Θ22(1)x2+Θ23(1)x3)
a 3 ( 2 ) = g ( Θ 30 ( 1 ) x 0 + Θ 31 ( 1 ) x 1 + Θ 32 ( 1 ) x 2 + Θ 33 ( 1 ) x 3 ) a_3^{(2)}=g(\Theta_{30}^{(1)}x_0+\Theta_{31}^{(1)}x_1+\Theta_{32}^{(1)}x_2+\Theta_{33}^{(1)}x_3) a3(2)=g(Θ30(1)x0+Θ31(1)x1+Θ32(1)x2+Θ33(1)x3)
注意,在layer2-layer3时,我们加了一个偏置单元 a 0 ( 2 ) = 1 a_0^{(2)}=1 a0(2)=1,这样之后
h Θ ( x ) = a 1 ( 3 ) = g ( Θ 10 ( 2 ) a 0 ( 2 ) + Θ 11 ( 2 ) a 1 ( 2 ) + Θ 22 ( 2 ) a 2 ( 2 ) + Θ 23 ( 2 ) a 3 ( 2 ) ) h_\Theta(x)=a_1^{(3)}=g(\Theta_{10}^{(2)}a_0^{(2)}+\Theta_{11}^{(2)}a_1^{(2)}+\Theta_{22}^{(2)}a_2^{(2)}+\Theta_{23}^{(2)}a_3^{(2)}) hΘ(x)=a1(3)=g(Θ10(2)a0(2)+Θ11(2)a1(2)+Θ22(2)a2(2)+Θ23(2)a3(2))
如果第j层的节点数是 s j s_j sj,第j+1层的节点数是 s j + 1 s_{j+1} sj+1,那么 Θ ( j ) \Theta^{(j)} Θ(j)的维度就是 ( s j + 1 × ( s j + 1 ) ) (s_{j+1}×(s_j+1)) (sj+1×(sj+1))
在计算过程中我们一般会添加一些偏置节点,但是要注意,这些节点是手动添加的,并非输出生成的。
2.2模型表示(2)
在这里,我们打算对2.1节中的层与层的连接进行一个向量化表示,我们用 z k ( j ) z_k^{(j)} zk(j)来表示激活函数g的输入内容,其中k表示节点序号,j表示网络层数,这样我们就把相应的函数表示修改为如下内容:
a 1 ( 2 ) = g ( z 1 ( 2 ) ) a_1^{(2)}=g(z_1^{(2)}) a1(2)=g(z1(2))
a 2 ( 2 ) = g ( z 2 ( 2 ) ) a_2^{(2)}=g(z_2^{(2)}) a2(2)=g(z2(2))
a 3 ( 2 ) = g ( z 3 ( 2 ) ) a_3^{(2)}=g(z_3^{(2)}) a3(2)=g(z3(2))
更直接一点,其实z也可以这样表示(e.g.):
z k ( 2 ) = Θ k 0 ( 1 ) x 0 + Θ k 1 ( 1 ) x 1 + Θ k 2 ( 1 ) x 2 + Θ k 3 ( 1 ) x 3 + . . . + Θ k n ( 1 ) x n z_k^{(2)}=\Theta_{k0}^{(1)}x_0+\Theta_{k1}^{(1)}x_1+\Theta_{k2}^{(1)}x_2+\Theta_{k3}^{(1)}x_3+...+\Theta_{kn}^{(1)}x_n zk(2)=Θk0(1)x0+Θk1(1)x1+Θk2(1)x2+Θk3(1)x3+...+Θkn(1)xn
其中,x可以向量化为 x = [ x 0 x 1 . . . x n − 1 x n ] x=\left[ \begin{matrix} x_0 \\ x_1 \\ ... \\ x_{n-1} \\ x_{n} \end{matrix} \right] x=⎣⎢⎢⎢⎢⎡x0x1...xn−1xn⎦⎥⎥⎥⎥⎤,z可以向量化为 z ( 2 ) = [ z 1 ( 2 ) z 2 ( 2 ) . . . z n ( 2 ) ] z^{(2)}=\left[\begin{matrix}z_1^{(2)}\\z_2^{(2)}\\...\\z_n^{(2)}\end{matrix}\right] z(2)=⎣⎢⎢⎢⎡z1(2)z2(2)...zn(2)⎦⎥⎥⎥⎤
我们令 x = a ( 1 ) x=a^{(1)} x=a(1),那么 z ( j ) = Θ ( j − 1 ) a ( j − 1 ) , a ( j ) = g ( z ( j ) ) z^{(j)}=\Theta^{(j-1)}a^{(j-1)},a^{(j)}=g(z^{(j)}) z(j)=Θ(j−1)a(j−1),a(j)=g(z(j))

3.应用
3.1示例和直觉(1)
我们已经了解了神经网络的基本模型,下面我们尝试用神经网络近似的表示一些基本的运算操作关系。
[ x 0 x 1 x 2 ] → [ g ( z ( 2 ) ) ] → h Θ ( x ) \begin{bmatrix}x_0\\x_1\\x_2\end{bmatrix}\rightarrow\begin{bmatrix}g(z^{(2)})\end{bmatrix} \rightarrow h_\Theta(x) ⎣⎡x0x1x2⎦⎤→[g(z(2))]→hΘ(x)(基本模型)
y = g ( z ) y=g(z) y=g(z):
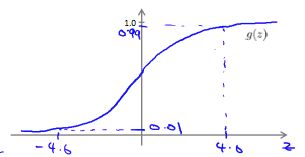
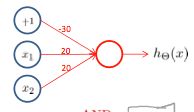
- “和(And)”操作
我们设置 Θ ( 1 ) = [ − 30 20 20 ] \Theta^{(1)}=[-30\;20\;20] Θ(1)=[−302020],那么 h Θ ( x ) = g ( − 30 + 20 x 1 + 20 x 2 ) h_\Theta(x)=g(-30+20x_1+20x_2) hΘ(x)=g(−30+20x1+20x2)
| x 1 x_1 x1 | x 2 x_2 x2 | h Θ ( x ) h_\Theta(x) hΘ(x) |
|---|---|---|
| 0 | 0 | ≈0 |
| 0 | 1 | ≈0 |
| 1 | 0 | ≈0 |
| 1 | 1 | ≈1 |
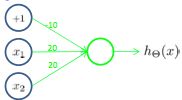
- “或(Or)”操作
我们设置 Θ ( 1 ) = [ − 10 20 20 ] \Theta^{(1)}=[-10\;20\;20] Θ(1)=[−102020],那么 h Θ ( x ) = g ( − 10 + 20 x 1 + 20 x 2 ) h_\Theta(x)=g(-10+20x_1+20x_2) hΘ(x)=g(−10+20x1+20x2)
| x 1 x_1 x1 | x 2 x_2 x2 | h Θ ( x ) h_\Theta(x) hΘ(x) |
|---|---|---|
| 0 | 0 | ≈0 |
| 0 | 1 | ≈1 |
| 1 | 0 | ≈1 |
| 1 | 1 | ≈1 |
3.1示例和直觉(2)
如果我们想实现同或操作(Xnor),我们就需要设置三层神经网络
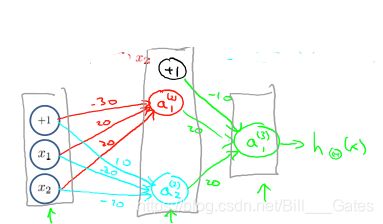
其中 Θ ( 1 ) = [ − 30 20 20 10 − 20 − 20 ] , Θ ( 2 ) = [ − 10 20 20 ] \Theta^{(1)}=[-30\;20\;20\;10\;-20\;-20],\Theta^{(2)}=[-10\;20\;20] Θ(1)=[−30202010−20−20],Θ(2)=[−102020]
| x 1 x_1 x1 | x 2 x_2 x2 | a 1 ( 2 ) a_1^{(2)} a1(2) | a 2 ( 2 ) a_2^{(2)} a2(2) | h Θ ( x ) h_\Theta(x) hΘ(x) |
|---|---|---|---|---|
| 0 | 0 | ≈0 | ≈1 | ≈1 |
| 0 | 1 | ≈0 | ≈0 | ≈0 |
| 1 | 0 | ≈0 | ≈0 | ≈0 |
| 1 | 1 | ≈1 | ≈0 | ≈1 |
3.3多类别分类
为了解决多分类问题,我们让我们的假设函数可以返回一个向量值,比如说,我们想要把我的数据分为四类,我们可以通过下面的这个例子看一看如何进行分类。该算法将图像作为输入,并对其进行相应的分类:
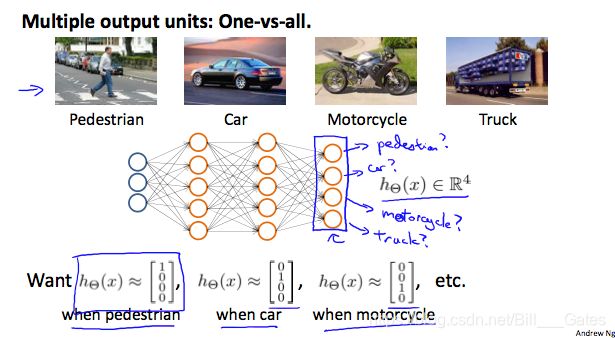
我们可以定义我们的结果类为:

每一个 y ( i ) y^{(i)} y(i)表示一个不同的相关图片(汽车,行人,货车,摩托车),在每一层的内部,都提供给我们一些新的信息,这些信息可以构成我们的假设函数,就像下面这样:
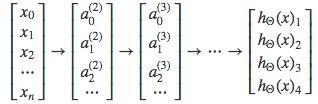
我们的一个集合输入的假设函数输出结果可能像类似于这样的: h Θ ( x ) = [ 0 0 0 0 ] h_\Theta(x)=[0\;0\;0\;0] hΘ(x)=[0000]
根据我们上述的例子中所描述的条件,我们可以知道,这个结果表示的是摩托车。
参考文献
链接: Coursera Machine Learning.