Leetcode 75算法题( 上)(使用C++实现)
目录
数组 / 字符串
1768.交替合并字符串
1071、字符串中的最大公因子
1431. 拥有最多糖果的孩子
605. 种花问题
345. 反转字符串中的元音字母
151. 反转字符串中的单词
238. 除自身以外数组的乘积
334. 递增的三元子序列
443. 压缩字符串
双指针
283. 移动零
392. 判断子序列
11. 盛最多水的容器
1679. K 和数对的最大数目
滑动窗口
1456. 定长子串中元音的最大数目
1004. 最大连续1的个数 III
1493. 删掉一个元素以后全为 1 的最长子数组
前缀和
1732. 找到最高海拔
724. 寻找数组的中心下标
哈希表 / 哈希集合
2215. 找出两数组的不同
1207. 独一无二的出现次数
给你一个整数数组 arr,请你帮忙统计数组中每个数的出现次数。
如果每个数的出现次数都是独一无二的,就返回 true;否则返回 false。
1657. 确定两个字符串是否接近
2352. 相等行列对
栈
2390. 从字符串中移除星号
735. 行星碰撞
394. 字符串解码
队列
933. 最近的请求次数
649. Dota2 参议院
链表
328. 奇偶链表
206. 反转链表
2130. 链表最大孪生和
二叉树 - 遍历方法
层次遍历
前序遍历
后序遍历
中序遍历
二叉树 - 深度优先搜索
104. 二叉树的最大深度
872. 叶子相似的树
1448. 统计二叉树中好节点的数目
437. 路径总和 III
1372. 二叉树中的最长交错路径
236. 二叉树的最近公共祖先
二叉树 - 广度优先搜索
199. 二叉树的右视图
1161. 最大层内元素和
二叉搜索树
700. 二叉搜索树中的搜索
450. 删除二叉搜索树中的节点
图-搜索方式
深度优先搜索算法
广度优先搜索算法
图 - 深度优先搜索
841. 钥匙和房间
547. 省份数量
1466. 重新规划路线
399. 除法求值
图 - 广度优先搜索
1926. 迷宫中离入口最近的出口
994. 腐烂的橘子
堆 / 优先队列
215. 数组中的第K个最大元素
2336. 无限集中的最小数字
2542. 最大子序列的分数
2462. 雇佣 K 位工人的总代价
二分查找
374. 猜数字大小
2300. 咒语和药水的成功对数
162. 寻找峰值
875. 爱吃香蕉的珂珂
数组 / 字符串
1768.交替合并字符串
两个字符串 word1 和 word2 。请你从 word1 开始,通过交替添加字母来合并字符串。如果一个字符串比另一个字符串长,就将多出来的字母追加到合并后字符串的末尾。
返回 合并后的字符串 。
代码如下:
class Solution {
public:
string mergeAlternately(string word1, string word2) {
string res = "";
int index = 0;
while (index < word1.length() || index < word2.length()) {
if (index < word1.length()) {
res += word1[index];
}
if (index < word2.length()) {
res += word2[index];
}
index++;
}
return res;
}
};
1071、字符串中的最大公因子
对于字符串 s 和 t,只有在 s = t + ... + t(t 自身连接 1 次或多次)时,我们才认定 “t 能除尽 s”。
给定两个字符串 str1 和 str2 。返回 最长字符串 x,要求满足 x 能除尽 str1 且 x 能除尽 str2 。
代码如下:
class Solution
{
public:
string gcdOfStrings(string str1, string str2)
{
if(str1+str2!=str2+str1)
return "";
else
return str1.substr(0,gcd(str1.size(),str2.size()));
}
int gcd(int a,int b)
{
return b==0?a:gcd(b,a%b);
}
};辗转相除法,也称为欧几里德算法,是用于计算两个整数的最大公约数(GCD)的一种常见方法。
基本原理是根据欧几里德定理,如果两个整数a和b满足b不为零,则它们的最大公约数等于 b和 a除以b的余数的最大公约数。这个过程不断迭代,直到余数为零,此时的除数即为最大公约数。
1431. 拥有最多糖果的孩子
代码如下:
class Solution {
public:
vector kidsWithCandies(vector& candies, int extraCandies) {
int Max = 0;
vector res;
Max = *max_element(candies.begin(),candies.end());
for(int i = 0;i=Max?true:false);
}
return res;
}
}; 605. 种花问题
假设有一个很长的花坛,一部分地块种植了花,另一部分却没有。可是,花不能种植在相邻的地块上,它们会争夺水源,两者都会死去。
给你一个整数数组 flowerbed 表示花坛,由若干 0 和 1 组成,其中 0 表示没种植花,1 表示种植了花。另有一个数 n ,能否在不打破种植规则的情况下种入 n 朵花?能则返回 true ,不能则返回 false 。
代码如下:
class Solution {
public:
bool canPlaceFlowers(vector& flowerbed, int n) {
int ans = 0;
for (int i = 0; i < flowerbed.size(); i++) {
//判断当前位置能否种花
//能种 ❀ 的情况
if (flowerbed[i] == 0
&& (i + 1 == flowerbed.size()|| flowerbed[i + 1] == 0)
&& (i == 0 || flowerbed[i - 1] == 0)) {
flowerbed[i] = 1;
ans++;
}
}
return ans >= n;
}
}; 345. 反转字符串中的元音字母
给你一个字符串 s ,仅反转字符串中的所有元音字母,并返回结果字符串。
元音字母包括 'a'、'e'、'i'、'o'、'u',且可能以大小写两种形式出现不止一次。
代码如下:
class Solution {
public:
string reverseVowels(string s)
{
string str = "aeiouAEIOU";
int l = 0; //左指针
int r = s.size()-1; //右指针
while(l151. 反转字符串中的单词
给你一个字符串 s ,请你反转字符串中 单词 的顺序。
单词 是由非空格字符组成的字符串。s 中使用至少一个空格将字符串中的 单词 分隔开。
返回 单词 顺序颠倒且 单词 之间用单个空格连接的结果字符串。
注意:输入字符串 s中可能会存在前导空格、尾随空格或者单词间的多个空格。返回的结果字符串中,单词间应当仅用单个空格分隔,且不包含任何额外的空格。
代码如下:
class Solution {
public:
string reverseWords(string s) {
int p1 = s.size() - 1, p2 = s.size() - 1;
string t = "";
while(p2 >= 0){
while(p1 >= 0 && s[p1]==' '){//循环清除左端的空格
p1--;
}
p2=p1;
while(p2 >= 0 && s[p2]!=' '){//循环清除右端的空格
p2--;
}
for(int i=p2+1; i<=p1; i++){
t += s[i];
}
t += ' ';
p1=p2;
cout<238. 除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。
题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。
请不要使用除法,且在 O(n) 时间复杂度内完成此题。
代码如下:
class Solution {
public:
vector productExceptSelf(vector& nums) {
int n=nums.size();
int left=1,right=1; //left:从左边累乘,right:从右边累乘
vector res(n,1); //定义长度为n的res,默认值为1
for(int i=0;i 334. 递增的三元子序列
给你一个整数数组 nums ,判断这个数组中是否存在长度为 3 的递增子序列。
如果存在这样的三元组下标 (i, j, k) 且满足 i < j < k ,使得 nums[i] < nums[j] < nums[k] ,返回 true ;否则,返回 false 。
代码如下:
class Solution {
public:
bool increasingTriplet(vector& nums) {
int a = INT_MAX;
int b = INT_MAX;
for (auto e : nums) {
if (e <= a) {
a = e;
} else if (e <= b) {
b = e;
} else {
return true;
}
}
return false;
}
}; 443. 压缩字符串
给你一个字符数组 chars ,请使用下述算法压缩:
从一个空字符串 s 开始。对于 chars 中的每组 连续重复字符 :
如果这一组长度为 1 ,则将字符追加到 s 中。
否则,需要向 s 追加字符,后跟这一组的长度。
压缩后得到的字符串 s 不应该直接返回 ,需要转储到字符数组 chars 中。需要注意的是,如果组长度为 10 或 10 以上,则在 chars 数组中会被拆分为多个字符。
请在 修改完输入数组后 ,返回该数组的新长度。
代码如下:
class Solution {
public:
int compress(vector& chars) {
int len = 0;
for (int i = 0, cnt = 1; i < chars.size(); i++, cnt++) {
if (i + 1 == chars.size() || chars[i] != chars[i + 1]) {
chars[len++] = chars[i];
if (cnt > 1) {
for (char ch : to_string(cnt)) {
chars[len++] = ch;
}
}
cnt = 0;
}
}
return len;
}
}; 双指针
283. 移动零
给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。
请注意 ,必须在不复制数组的情况下原地对数组进行操作。
class Solution {
public:
//把零删了后面再补,也是双指针
void moveZeroes(vector& nums) {
int slow = 0;
for(auto fast : nums)
if(fast != 0)
nums[slow++] = fast;
for(;slow < nums.size(); ++slow) {
nums[slow] = 0;
}
}
}; 392. 判断子序列
给定字符串 s 和 t ,判断 s 是否为 t 的子序列。
字符串的一个子序列是原始字符串删除一些(也可以不删除)字符而不改变剩余字符相对位置形成的新字符串。(例如,"ace"是"abcde"的一个子序列,而"aec"不是)。
进阶:
如果有大量输入的 S,称作 S1, S2, ... , Sk 其中 k >= 10亿,你需要依次检查它们是否为 T 的子序列。在这种情况下,你会怎样改变代码?
示例代码:
class Solution {
public:
bool isSubsequence(string s, string t) {
int i = 0;
for (int j = 0; i < s.length() && j < t.length(); j++) {
if (s[i] == t[j]) {
i++;
}
}
return i == s.length();
}
};11. 盛最多水的容器
给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。
找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
返回容器可以储存的最大水量。
说明:你不能倾斜容器。
示例代码:
class Solution {
public:
int maxArea(vector& height) {
int size = height.size();
int left=0, right=size-1;
int ans = 0;
while(left < right){
ans = max(ans, (right-left)*min(height[left], height[right]));
if(height[left] > height[right])
--right;
else
++left;
}
return ans;
}
}; 1679. K 和数对的最大数目
给你一个整数数组 nums 和一个整数 k 。
每一步操作中,你需要从数组中选出和为 k 的两个整数,并将它们移出数组。
返回你可以对数组执行的最大操作数。
示例代码如下:
class Solution {
public:
int maxOperations(vector& nums, int k) {
//排序
sort(nums.begin(),nums.end());
int ans=0;
int l=0,r=nums.size()-1; //左右指针吗指向两边
while(lk)
{
r--;
}
else {
ans++ ,l++,r--;
}
}
return ans;
} 滑动窗口
643. 子数组最大平均数 I
给你一个由 n 个元素组成的整数数组 nums 和一个整数 k 。
请你找出平均数最大且 长度为 k 的连续子数组,并输出该最大平均数。
任何误差小于 10-5 的答案都将被视为正确答案。
代码如下:
class Solution {
public:
double findMaxAverage(vector& nums, int k) {
int sum = 0,maxi=INT_MIN;
for(int i=0;i=k)
{
sum-=nums[i-k];
}
if(i+1>=k)
{
maxi=max(sum,maxi);
}
}
return maxi/(double)k;
}
}; 1456. 定长子串中元音的最大数目
给你字符串 s 和整数 k 。
请返回字符串 s 中长度为 k 的单个子字符串中可能包含的最大元音字母数。
英文中的 元音字母 为(a, e, i, o, u)。
代码如下:
class Solution {
public:
int maxVowels(string s, int k)
{
//双指针法,滑动窗口、快慢指针
int maxVow = INT32_MIN;
int mySize = 0;//最大元音字母数
int j = 0;
for(int i = 0; i < s.size(); i++)
{
if(s[i] == 'a' || s[i] == 'e' ||
s[i] == 'i' || s[i] == 'o' || s[i] == 'u')
{
mySize++;
}
if(i - j + 1 == k)
{
if(mySize > maxVow)
maxVow = mySize;
if(s[j] == 'a' || s[j] == 'e' ||
s[j] == 'i' || s[j] == 'o' || s[j] == 'u')
{
mySize--;
j++;
}else
{
j++;
}
}
}
return maxVow;
}
};1004. 最大连续1的个数 III
给定一个二进制数组 nums 和一个整数 k,如果可以翻转最多 k 个 0 ,则返回 数组中连续 1 的最大个数 。
代码如下:
class Solution {
public:
int longestOnes(vector& nums, int k)
{
int left =0,right=0;
int res =0;
while(right 1493. 删掉一个元素以后全为 1 的最长子数组
给你一个二进制数组 nums ,你需要从中删掉一个元素。
请你在删掉元素的结果数组中,返回最长的且只包含 1 的非空子数组的长度。
如果不存在这样的子数组,请返回 0 。
代码如下:
class Solution {
public:
int longestSubarray(vector& nums)
{
int maxn = 0, l = 0, r = 0;
for(int i = 0; i < nums.size(); i++)
{
if(nums[i] == 1)
{
r++;
}
else if(nums[i] == 0)
{
l = r;
r = 0;
}
maxn = max(maxn,l+r);
}
if(maxn == nums.size())
return maxn-1;
else
return maxn;
}
}; 前缀和
1732. 找到最高海拔
有一个自行车手打算进行一场公路骑行,这条路线总共由 n + 1 个不同海拔的点组成。自行车手从海拔为 0 的点 0 开始骑行。
给你一个长度为 n 的整数数组 gain ,其中 gain[i] 是点 i 和点 i + 1 的 净海拔高度差(0 <= i < n)。请你返回最高点的海拔 。
代码如下:
class Solution {
public:
int largestAltitude(vector& gain) {
int res =0,height =0;
for(int g=0;g 备注:这道题一开始看上去不太好理解,其实就是求一个数组中前n个数的最大累加和
724. 寻找数组的中心下标
给你一个整数数组 nums ,请计算数组的 中心下标 。
数组 中心下标 是数组的一个下标,其左侧所有元素相加的和等于右侧所有元素相加的和。
如果中心下标位于数组最左端,那么左侧数之和视为 0 ,因为在下标的左侧不存在元素。这一点对于中心下标位于数组最右端同样适用。
如果数组有多个中心下标,应该返回 最靠近左边 的那一个。如果数组不存在中心下标,返回 -1 。
代码如下:
class Solution { //思路:左求和*2+中心索引值 = 总和
public:
int pivotIndex(vector& nums) {
int sum = 0;
int sumleft = 0;
int len=size(nums); //nums.size()
for(int i=0;i 哈希表 / 哈希集合
2215. 找出两数组的不同
给你两个下标从 0 开始的整数数组 nums1 和 nums2 ,请你返回一个长度为 2 的列表 answer ,其中:
answer[0] 是 nums1 中所有 不 存在于 nums2 中的 不同 整数组成的列表。
answer[1] 是 nums2 中所有 不 存在于 nums1 中的 不同 整数组成的列表。
注意:列表中的整数可以按 任意 顺序返回。
代码如下:
class Solution {
public:
vector> findDifference(vector& nums1, vector& nums2) {
unordered_set n1,n2; //去重
for(int n:nums1)
n1.insert(n);
for(int n:nums2)
n2.insert(n);
vector v1,v2;
for(int n:n1)
{
if(!n2.count(n))
v1.push_back(n);
}
for(int n:n2)
{
if(!n1.count(n))
v2.push_back(n);
}
vector > ans;
ans.push_back(v1);
ans.push_back(v2);
return ans;
}
}; 1207. 独一无二的出现次数
给你一个整数数组 arr,请你帮忙统计数组中每个数的出现次数。
如果每个数的出现次数都是独一无二的,就返回 true;否则返回 false。
代码如下:
class Solution {
public:
bool uniqueOccurrences(vector& arr) {
vector v1; // 存储数字的出现字数
int count = 0; // 统计数字的出现字数
sort(arr.begin(), arr.end()); // 排序,从小到大
// arr.emplace_back(0); // 取位补0
for(int i=0; i 1657. 确定两个字符串是否接近
如果可以使用以下操作从一个字符串得到另一个字符串,则认为两个字符串 接近 :
操作 1:交换任意两个 现有 字符。
例如,abcde -> aecdb
操作 2:将一个现有字符的每次出现转换为另一个现有字符,并对另一个字符执行相同的操作。
例如,aacabb -> bbcbaa(所有 a 转化为 b ,而所有的 b 转换为 a )
你可以根据需要对任意一个字符串多次使用这两种操作。
给你两个字符串,word1 和 word2 。如果 word1 和 word2 接近 ,就返回 true ;否则,返回 false 。
代码如下:
class Solution {
public:
bool closeStrings(string word1, string word2) {
int sz1 = word1.size(), sz2 = word2.size();
if (sz1 != sz2) return false; //1、长度不同,不会相近
vector rc1(26, 0), rc2(26, 0); //初始化两个数组,长度为26
for (int i = 0; i < sz1; ++i) { //先统计每个字符出现的次数
rc1[word1[i] - 'a']++;
rc2[word2[i] - 'a']++;
}
for (int i = 0; i < 26; i++) {
if (rc1[i] == 0 && rc2[i] != 0 || rc1[i] != 0 && rc2[i] == 0) return false;
}
sort(rc1.begin(), rc1.end());
sort(rc2.begin(), rc2.end());
return rc1 == rc2;
}
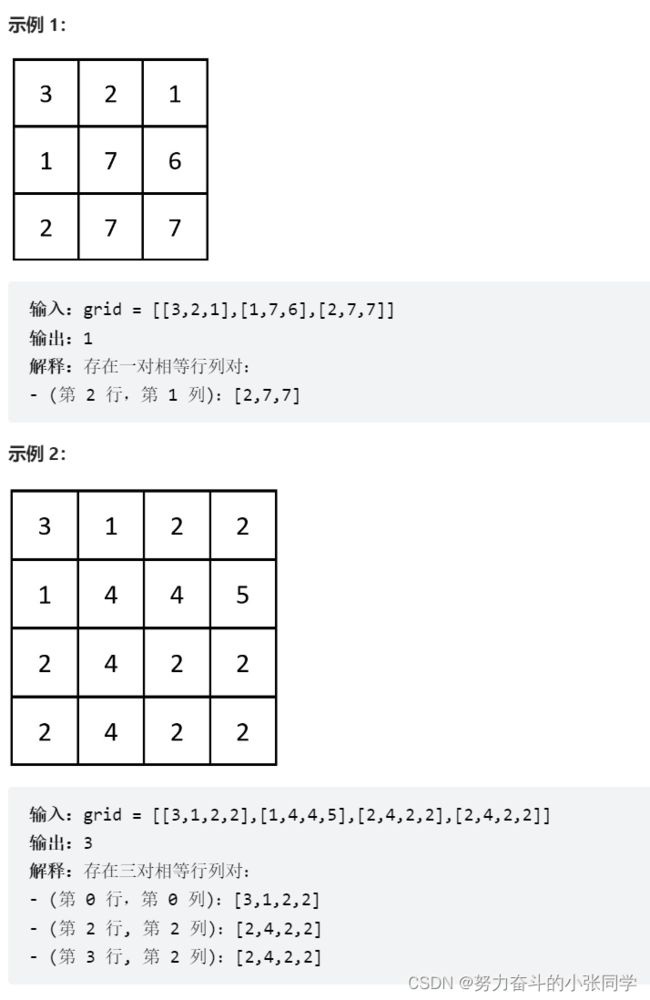
}; 2352. 相等行列对
给你一个下标从 0 开始、大小为 n x n 的整数矩阵 grid ,返回满足 Ri 行和 Cj 列相等的行列对 (Ri, Cj) 的数目。
如果行和列以相同的顺序包含相同的元素(即相等的数组),则认为二者是相等的。
代码如下:
class Solution {
public:
int equalPairs(vector>& grid) {
int ans = 0;
vector> grid2(grid.size(), vector(grid.size()));
for (int i = 0; i < grid.size(); i++)
for (int j = 0; j < grid.size(); j++)
grid2[i][j] = grid[j][i];
for (int i = 0; i < grid.size(); i++)
for (int j = 0; j < grid.size(); j++)
if (grid[i] == grid2[j])
ans++;
return ans;
}
}; 栈
2390. 从字符串中移除星号
给你一个包含若干星号 * 的字符串 s 。
在一步操作中,你可以:
选中 s 中的一个星号。
移除星号 左侧 最近的那个 非星号 字符,并移除该星号自身。
返回移除 所有 星号之后的字符串。
注意:
生成的输入保证总是可以执行题面中描述的操作。
可以证明结果字符串是唯一的。
代码如下:
class Solution {
public:
string removeStars(string s) {
//不用栈,双指针也可以做
string ans;
for(int i = 0; i < s.size(); i++) {
if(s[i] != '*') {
ans += s[i];
}else {
ans.pop_back(); //string可以使用pop_back()
}
}
return ans;
}
};735. 行星碰撞
给定一个整数数组 asteroids,表示在同一行的行星。
对于数组中的每一个元素,其绝对值表示行星的大小,正负表示行星的移动方向(正表示向右移动,负表示向左移动)。每一颗行星以相同的速度移动。
找出碰撞后剩下的所有行星。碰撞规则:两个行星相互碰撞,较小的行星会爆炸。如果两颗行星大小相同,则两颗行星都会爆炸。两颗移动方向相同的行星,永远不会发生碰撞。
class Solution {
public:
vector asteroidCollision(vector& asteroids) {
vector resVec;//存储结果
for(auto asteroid:asteroids)
{
if(resVec.empty())
{
resVec.push_back(asteroid);
}
else if(resVec.back() >0 && asteroid <0)
{
//第五种情况:序列的最尾端是正数,nextItem <0; 这时方向相对,两个方向的行星必定会产生碰撞
while( !resVec.empty() && resVec.back() >0 && asteroid <0)
{
int sum = resVec.back() + asteroid;
if (sum < 0){
//此时代表序列的尾端的绝对值比较小,所以栈顶的行星爆炸
resVec.pop_back();
}
else if (sum == 0){
//此时代表序列的尾端的绝对值与asteroid的绝对值相等,两个同时爆炸
resVec.pop_back();
asteroid = INT_MAX;//表示asteroid这个行星爆炸了
break;
}
else{
//此时表示asteroid的绝对值比较小,只爆炸asteroid
asteroid = INT_MAX;//表示asteroid这个行星爆炸了
break;
}
}
//退出循环,如果asteroid还没有爆炸,放入栈顶
if (asteroid != INT_MAX){
resVec.push_back(asteroid);
}
}
else{
//第二、三、四种情况都不会产生碰撞,直接放入
resVec.push_back(asteroid);
}
}
return resVec;
}
}; 394. 字符串解码
给定一个经过编码的字符串,返回它解码后的字符串。
编码规则为: k[encoded_string],表示其中方括号内部的 encoded_string 正好重复 k 次。注意 k 保证为正整数。
你可以认为输入字符串总是有效的;输入字符串中没有额外的空格,且输入的方括号总是符合格式要求的。
此外,你可以认为原始数据不包含数字,所有的数字只表示重复的次数 k ,例如不会出现像 3a 或 2[4] 的输入。
代码如下:
class Solution {
public:
string decodeString(string s) {
int len = s.size();
int num = 0;
stack numstack;
stack strstack;
string cur = "";
string result = "";
for(int i=0; i='0' && s[i]<='9')
{
num = 10*num + s[i] - '0';
}
else if(s[i] == '[')
{
numstack.push(num);
strstack.push(cur);
num = 0;
cur.clear();
}
else if((s[i]>='a' && s[i]<='z') || (s[i]>='A' && s[i]<='Z'))
cur += s[i];
else if(s[i] == ']')
{
int k = numstack.top();
numstack.pop();
for(int j=0; j 队列
933. 最近的请求次数
写一个 RecentCounter 类来计算特定时间范围内最近的请求。
请你实现 RecentCounter 类:
RecentCounter() 初始化计数器,请求数为 0 。
int ping(int t) 在时间 t 添加一个新请求,其中 t 表示以毫秒为单位的某个时间,并返回过去 3000 毫秒内发生的所有请求数(包括新请求)。确切地说,返回在 [t-3000, t] 内发生的请求数。
保证 每次对 ping 的调用都使用比之前更大的 t 值。
代码如下:
static const auto io_sync_off = []() {
// 关闭同步
ios::sync_with_stdio(false);
// 关闭cin和cout流的绑定
cin.tie(nullptr);
cout.tie(nullptr);
return nullptr;
}();
class RecentCounter {
private:
queue qu;
public:
RecentCounter() {
}
int ping(int t) {
qu.emplace(t);
while (qu.front() < t - 3000) {
qu.pop();
}
return qu.size();
}
}; 备注:阅读理解
649. Dota2 参议院
Dota2 的世界里有两个阵营:Radiant(天辉)和 Dire(夜魇)
Dota2 参议院由来自两派的参议员组成。现在参议院希望对一个 Dota2 游戏里的改变作出决定。他们以一个基于轮为过程的投票进行。在每一轮中,每一位参议员都可以行使两项权利中的 一 项:
禁止一名参议员的权利:参议员可以让另一位参议员在这一轮和随后的几轮中丧失 所有的权利 。
宣布胜利:如果参议员发现有权利投票的参议员都是 同一个阵营的 ,他可以宣布胜利并决定在游戏中的有关变化。
给你一个字符串 senate 代表每个参议员的阵营。字母 'R' 和 'D'分别代表了 Radiant(天辉)和 Dire(夜魇)。然后,如果有 n 个参议员,给定字符串的大小将是 n。
以轮为基础的过程从给定顺序的第一个参议员开始到最后一个参议员结束。这一过程将持续到投票结束。所有失去权利的参议员将在过程中被跳过。
假设每一位参议员都足够聪明,会为自己的政党做出最好的策略,你需要预测哪一方最终会宣布胜利并在 Dota2 游戏中决定改变。输出应该是 "Radiant" 或 "Dire" 。
代码如下:
class Solution {
public:
string predictPartyVictory(string senate) {
bool R=true,D=true;
int flag =0; //当flag大于0时,R在D前出现,R可以消灭D。当flag小于0时,D在R前出现,D可以消灭R
while(R && D)
{
R=false;
D=false;
for(int i=0;i0) senate[i] =0;
else D=true;
flag --;
}
}
}
// 循环结束之后,R和D只能有一个为true
return R == true ? "Radiant" : "Dire";
}
}; 链表
给你一个链表的头节点 head 。删除链表的中间节点 ,并返回修改后的链表的头节点 head 。
长度为 n 链表的中间节点是从头数起第 ⌊n / 2⌋ 个节点(下标从 0 开始),其中 ⌊x⌋ 表示小于或等于 x 的最大整数。
对于 n = 1、2、3、4 和 5 的情况,中间节点的下标分别是 0、1、1、2 和 2 。
代码如下:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* deleteMiddle(ListNode* head) {
//快慢指针
ListNode* dummpy = new ListNode(0,head);
ListNode* fast = dummpy;
ListNode* slow = dummpy;
if(fast == nullptr) return nullptr;
while(fast && fast->next && fast->next->next)
{
fast = fast->next->next;
slow = slow->next;
}
slow->next = slow->next->next;
return dummpy->next;
}
};328. 奇偶链表
给定单链表的头节点 head ,将所有索引为奇数的节点和索引为偶数的节点分别组合在一起,然后返回重新排序的列表。
第一个节点的索引被认为是 奇数 , 第二个节点的索引为 偶数 ,以此类推。
请注意,偶数组和奇数组内部的相对顺序应该与输入时保持一致。
你必须在 O(1) 的额外空间复杂度和 O(n) 的时间复杂度下解决这个问题。
代码如下:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* oddEvenList(ListNode* head) {
if (!head || !head->next)
return head;
ListNode* odd = head;
ListNode* even = head->next;
ListNode* evenHead =even;
while(even && even->next)
{
odd->next =even->next;
odd = odd->next;
even->next = odd->next;
even = even->next;
}
odd->next = evenHead;
return head;
}
};206. 反转链表
给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。
代码如下:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* reverseList(ListNode* head) {
ListNode* prev = nullptr; //前指针节点
ListNode* curr = head; // 当前指针节点
//每次循环,都将当前节点指向它前面的节点,然后当前节点和前节点后移
while(curr)
{
ListNode* nextTemp = curr->next;//临时节点,暂存当前节点的下一节点,用于后移
curr->next = prev; //将当前节点指向它前面的节点
prev = curr; //前指针后移
curr = nextTemp; //当前指针后移
}
return prev;
}
};2130. 链表最大孪生和
在一个大小为 n 且 n 为 偶数 的链表中,对于 0 <= i <= (n / 2) - 1 的 i ,第 i 个节点(下标从 0 开始)的孪生节点为第 (n-1-i) 个节点 。
比方说,n = 4 那么节点 0 是节点 3 的孪生节点,节点 1 是节点 2 的孪生节点。这是长度为 n = 4 的链表中所有的孪生节点。
孪生和 定义为一个节点和它孪生节点两者值之和。
给你一个长度为偶数的链表的头节点 head ,请你返回链表的 最大孪生和 。
代码如下:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
int pairSum(ListNode* head) {
if(!head) return 0;
ListNode* fast = head;
ListNode* slow = head;
//1.快慢指针,寻找链表中点
while(fast && fast->next )
{
fast = fast->next->next;
slow = slow->next;
}//如果链表的节点数是奇数,slow指针将指向中间节点;如果节点数是偶数,slow指针将指向靠近链表中心的前一个节点。
//2.反转后半链表
ListNode* curr = slow;
ListNode* prev = nullptr;
while(curr)
{
ListNode* temp = curr->next;
curr->next = prev;
prev = curr;
curr = temp;
}
//计算孪生和
int maxTwinSum = 0;
while(head && prev)
{
maxTwinSum = max(maxTwinSum, head->val + prev->val);
head = head->next;
prev = prev->next;
}
return maxTwinSum;
}
};二叉树 - 遍历方法
层次遍历
#include
#include
using namespace std;
// 二叉树节点的定义
struct TreeNode {
int val;
TreeNode* left;
TreeNode* right;
TreeNode(int value) : val(value), left(nullptr), right(nullptr) {}
};
// 层次遍历函数
void levelOrderTraversal(TreeNode* root) {
if (root == nullptr)
return;
queue q;
q.push(root);
while (!q.empty()) {
TreeNode* curr = q.front();
q.pop();
cout << curr->val << " ";
if (curr->left != nullptr)
q.push(curr->left);
if (curr->right != nullptr)
q.push(curr->right);
}
}
int main() {
// 创建二叉树
TreeNode* root = new TreeNode(1);
root->left = new TreeNode(2);
root->right = new TreeNode(3);
root->left->left = new TreeNode(4);
root->left->right = new TreeNode(5);
// 层次遍历二叉树
cout << "层次遍历结果:";
levelOrderTraversal(root);
cout << endl;
// 释放内存
delete root->left->left;
delete root->left->right;
delete root->left;
delete root->right;
delete root;
return 0;
}
前序遍历
#include
using namespace std;
// 二叉树节点的定义
struct TreeNode {
int val;
TreeNode* left;
TreeNode* right;
TreeNode(int value) : val(value), left(nullptr), right(nullptr) {}
};
// 前序遍历函数
void preorderTraversal(TreeNode* root) {
if (root == nullptr)
return;
cout << root->val << " "; // 输出当前节点的值
preorderTraversal(root->left); // 递归遍历左子树
preorderTraversal(root->right); // 递归遍历右子树
}
int main() {
// 创建二叉树
TreeNode* root = new TreeNode(1);
root->left = new TreeNode(2);
root->right = new TreeNode(3);
root->left->left = new TreeNode(4);
root->left->right = new TreeNode(5);
// 前序遍历二叉树
cout << "前序遍历结果:";
preorderTraversal(root);
cout << endl;
// 释放内存
delete root->left->left;
delete root->left->right;
delete root->left;
delete root->right;
delete root;
return 0;
}
后序遍历
#include
using namespace std;
// 二叉树节点的定义
struct TreeNode {
int val;
TreeNode* left;
TreeNode* right;
TreeNode(int value) : val(value), left(nullptr), right(nullptr) {}
};
// 后序遍历函数
void postorderTraversal(TreeNode* root) {
if (root == nullptr)
return;
postorderTraversal(root->left); // 递归遍历左子树
postorderTraversal(root->right); // 递归遍历右子树
cout << root->val << " "; // 输出当前节点的值
}
int main() {
// 创建二叉树
TreeNode* root = new TreeNode(1);
root->left = new TreeNode(2);
root->right = new TreeNode(3);
root->left->left = new TreeNode(4);
root->left->right = new TreeNode(5);
// 后序遍历二叉树
cout << "后序遍历结果:";
postorderTraversal(root);
cout << endl;
// 释放内存
delete root->left->left;
delete root->left->right;
delete root->left;
delete root->right;
delete root;
return 0;
}
中序遍历
#include
using namespace std;
// 二叉树节点的定义
struct TreeNode {
int val;
TreeNode* left;
TreeNode* right;
TreeNode(int value) : val(value), left(nullptr), right(nullptr) {}
};
// 中序遍历函数
void inorderTraversal(TreeNode* root) {
if (root == nullptr)
return;
inorderTraversal(root->left); // 递归遍历左子树
cout << root->val << " "; // 输出当前节点的值
inorderTraversal(root->right); // 递归遍历右子树
}
int main() {
// 创建二叉树
TreeNode* root = new TreeNode(1);
root->left = new TreeNode(2);
root->right = new TreeNode(3);
root->left->left = new TreeNode(4);
root->left->right = new TreeNode(5);
// 中序遍历二叉树
cout << "中序遍历结果:";
inorderTraversal(root);
cout << endl;
// 释放内存
delete root->left->left;
delete root->left->right;
delete root->left;
delete root->right;
delete root;
return 0;
}
二叉树 - 深度优先搜索
104. 二叉树的最大深度
给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
代码如下:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
// //1.递归
// int maxDepth(TreeNode* root) {
// if(root == nullptr) return 0;
// return max(maxDepth(root->left),maxDepth(root->right))+1;
// }
int maxDepth(TreeNode* root)
{
if(root == nullptr) return 0;
int num=0;
queue que;
que.push(root);
while(!que.empty())
{
int n =que.size();
for(int i =0;ileft)
{
que.push(curr->left);
}
if(curr->right)
{
que.push(curr->right);
}
que.pop();
}
num++;
}
return num;
}
}; 872. 叶子相似的树
请考虑一棵二叉树上所有的叶子,这些叶子的值按从左到右的顺序排列形成一个 叶值序列 。
举个例子,如上图所示,给定一棵叶值序列为 (6, 7, 4, 9, 8) 的树。
如果有两棵二叉树的叶值序列是相同,那么我们就认为它们是 叶相似 的。
如果给定的两个根结点分别为 root1 和 root2 的树是叶相似的,则返回 true;否则返回 false 。
代码如下:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector store1;
vector store2;
void dfs1(TreeNode* root)
{
if(root==NULL)
return;
dfs1(root->left);
dfs1(root->right);
if(root->left==NULL&&root->right==NULL)
store1.push_back(root->val);
}
void dfs2(TreeNode* root)
{
if(root==NULL)
return;
if(root->left==NULL&&root->right==NULL)
store2.push_back(root->val);
dfs2(root->left);
dfs2(root->right);
}
bool leafSimilar(TreeNode* root1, TreeNode* root2)
{
dfs1(root1);
dfs2(root2);
if(store1.size()!=store2.size())
return false;
for(int i=0;i 1448. 统计二叉树中好节点的数目
给你一棵根为 root 的二叉树,请你返回二叉树中好节点的数目。
「好节点」X 定义为:从根到该节点 X 所经过的节点中,没有任何节点的值大于 X 的值。
代码如下:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int goodNodes(TreeNode* root) {
int res = 1;
queue que;
que.push(root);
while(que.size()){
TreeNode* head = que.front();
que.pop();
if(head->left){
que.push(head->left);
if(head->left->val >= head->val) res++;
else head->left->val = head->val;
}
if(head->right){
que.push(head->right);
if(head->right->val >= head->val) res++;
else head->right->val = head->val;
}
}
return res;
}
}; 437. 路径总和 III
给定一个二叉树的根节点 root ,和一个整数 targetSum ,求该二叉树里节点值之和等于 targetSum 的 路径 的数目。
路径 不需要从根节点开始,也不需要在叶子节点结束,但是路径方向必须是向下的(只能从父节点到子节点)。
代码如下:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
private:
int ans=0;
public:
int pathSum(TreeNode* root, int targetSum) {
if(!root) return 0;
dfs(root,targetSum);
pathSum(root->left, targetSum);
pathSum(root->right, targetSum);
return ans;
}
void dfs(TreeNode* root, long targetSum)
{
targetSum -= root->val;
if(targetSum == 0)ans++;
if(!root->left && !root->right) return;
if(root->right) dfs(root->right, targetSum);
if(root->left) dfs(root->left, targetSum);
}
};1372. 二叉树中的最长交错路径
给你一棵以 root 为根的二叉树,二叉树中的交错路径定义如下:
选择二叉树中 任意 节点和一个方向(左或者右)。
如果前进方向为右,那么移动到当前节点的的右子节点,否则移动到它的左子节点。
改变前进方向:左变右或者右变左。
重复第二步和第三步,直到你在树中无法继续移动。
交错路径的长度定义为:访问过的节点数目 - 1(单个节点的路径长度为 0 )。
请你返回给定树中最长 交错路径 的长度。
代码如下:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
private:
int maxZigZag =0;
public:
int longestZigZag(TreeNode* root) {
dfs(root, true);
return maxZigZag ;
}
int dfs(TreeNode* root, bool isleft)
{
if(root ==nullptr) return 0;
int r = dfs(root->right, false);
int l = dfs(root->left, true);
int big = l > r ? l: r;
if(big > maxZigZag)
maxZigZag = big;
if(isleft)
return r + 1;
else
return l + 1;
}
};236. 二叉树的最近公共祖先
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。
代码如下:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if(root ==q || root ==p || !root) return root;
TreeNode* left = lowestCommonAncestor(root->left, p,q);
TreeNode* right = lowestCommonAncestor(root->right, p,q);
if(!left && !right) return nullptr;
else if(!left) return right;
else if(!right) return left;
return root;
}
};二叉树 - 广度优先搜索
199. 二叉树的右视图
给定一个二叉树的 根节点 root,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。
代码如下:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector rightSideView(TreeNode* root) {
//使用层序遍历,并只保留每层最后一个节点的值
vector ans;
if(!root)
return ans;
TreeNode* lastNode = root;
TreeNode* newLastNode = nullptr;
queue que;
que.push(root);
while(!que.empty())
{
TreeNode* curNode = que.front();
que.pop();
if(curNode->left)
{
que.push(curNode->left);
newLastNode = curNode->left;
}
if(curNode->right)
{
que.push(curNode->right);
newLastNode = curNode->right;
}
if(curNode == lastNode)
{
ans.push_back(curNode->val);
lastNode = newLastNode;
}
}
return ans;
}
}; 1161. 最大层内元素和
给你一个二叉树的根节点 root。设根节点位于二叉树的第 1 层,而根节点的子节点位于第 2 层,依此类推。
请返回层内元素之和 最大 的那几层(可能只有一层)的层号,并返回其中 最小 的那个。
代码如下:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int maxLevelSum(TreeNode* root) {
queue que;
que.push(root);
int ans=INT_MIN,i=0,h=1;
while(!que.empty())
{
int n=que.size();
int t=0;
while(n--)
{
TreeNode* x=que.front();
que.pop();
t+=x->val;
if(x->left) que.push(x->left);
if(x->right) que.push(x->right);
}
if(t>ans)
{
ans=t;
i=h;
}
h++;
}
return i;
}
}; 二叉搜索树
700. 二叉搜索树中的搜索
给定二叉搜索树(BST)的根节点 root 和一个整数值 val。
你需要在 BST 中找到节点值等于 val 的节点。 返回以该节点为根的子树。 如果节点不存在,则返回 null 。
代码如下:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
//方法1:
// TreeNode* searchBST(TreeNode* root, int val) {
// if(!root)
// {
// return nullptr;
// }
// if(root->val == val)
// {
// return root;
// }
// TreeNode* left_node = searchBST(root->left,val);
// TreeNode* right_node = searchBST(root->right,val);
// if(left_node) return left_node;
// if(right_node) return right_node;
// return nullptr;
// }
//迭代法2:
TreeNode* searchBST(TreeNode* root, int val)
{
while(root)
{
if(root->val > val) root = root->left;
else if(root->val < val) root = root->right;
else return root;
}
return nullptr;
}
};450. 删除二叉搜索树中的节点
给定一个二叉搜索树的根节点 root 和一个值 key,删除二叉搜索树中的 key 对应的节点,并保证二叉搜索树的性质不变。返回二叉搜索树(有可能被更新)的根节点的引用。
一般来说,删除节点可分为两个步骤:
首先找到需要删除的节点;
如果找到了,删除它。
代码如下:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* deleteNode(TreeNode* root, int key) {
// 第一种情况:没找到删除的节点,遍历到空节点直接返回了
if(root == nullptr) return root;
if(root->val == key)
{
// 第二种情况:左右孩子都为空(叶子节点),直接删除节点, 返回NULL为根节点
if(!root->left && !root->right)
{
delete root;
return nullptr;
}
// 第三种情况:其左孩子为空,右孩子不为空,删除节点,右孩子补位 ,返回右孩子为根节点
else if(!root->left)
{
auto retNode = root->right;
delete root;
return retNode;
}
// 第四种情况:其右孩子为空,左孩子不为空,删除节点,左孩子补位 ,返回左孩子为根节点
else if(!root->right)
{
auto retNode = root->left;
delete root;
return retNode;
}
// 第五种情况:左右孩子节点都不为空,则将删除节点的左子树放到删除节点的右子树的最左面节点的左孩子的位置
// 并返回删除节点右孩子为新的根节点。
else{
TreeNode* cur = root->right; // 找右子树最左面的节点
while(cur->left)
{
cur = cur->left;
}
cur->left = root->left;
TreeNode* tmp = root;
root = root->right; // 返回旧root的右孩子作为新root
delete tmp;
return root;
}
}
if(root->val > key) root->left = deleteNode(root->left, key);
if(root->val < key) root->right = deleteNode(root->right, key);
return root;
}
};图-搜索方式
深度优先搜索算法
#include
#include
#include
using namespace std;
void dfs(vector>& graph, vector& visited, int node) {
// 标记当前节点为已访问
visited[node] = true;
cout << node << " ";
// 遍历当前节点的邻居节点
for (int neighbor : graph[node]) {
// 如果邻居节点未被访问,则递归调用DFS函数
if (!visited[neighbor]) {
dfs(graph, visited, neighbor);
}
}
}
int main() {
int numNodes, numEdges;
cout << "Enter the number of nodes: ";
cin >> numNodes;
cout << "Enter the number of edges: ";
cin >> numEdges;
vector> graph(numNodes); // 二维向量表示图的邻接表
vector visited(numNodes, false); // 记录节点的访问状态
cout << "Enter the edges:\n";
for (int i = 0; i < numEdges; i++) {
int u, v;
cin >> u >> v;
// 无向图,添加两个方向的边
graph[u].push_back(v);
graph[v].push_back(u);
}
int startNode;
cout << "Enter the start node: ";
cin >> startNode;
cout << "DFS traversal starting from node " << startNode << ": ";
dfs(graph, visited, startNode);
cout << endl;
return 0;
}
广度优先搜索算法
#include
#include
#include
using namespace std;
void bfs(vector>& graph, vector& visited, int startNode) {
queue q;
q.push(startNode);
visited[startNode] = true;
while (!q.empty()) {
int currentNode = q.front();
q.pop();
cout << currentNode << " ";
for (int neighbor : graph[currentNode]) {
if (!visited[neighbor]) {
q.push(neighbor);
visited[neighbor] = true;
}
}
}
}
int main() {
int numNodes, numEdges;
cout << "Enter the number of nodes: ";
cin >> numNodes;
cout << "Enter the number of edges: ";
cin >> numEdges;
vector> graph(numNodes); // 二维向量表示图的邻接表
vector visited(numNodes, false); // 记录节点的访问状态
cout << "Enter the edges:\n";
for (int i = 0; i < numEdges; i++) {
int u, v;
cin >> u >> v;
// 无向图,添加两个方向的边
graph[u].push_back(v);
graph[v].push_back(u);
}
int startNode;
cout << "Enter the start node: ";
cin >> startNode;
cout << "BFS traversal starting from node " << startNode << ": ";
bfs(graph, visited, startNode);
cout << endl;
return 0;
}
图 - 深度优先搜索
841. 钥匙和房间
有 n 个房间,房间按从 0 到 n - 1 编号。最初,除 0 号房间外的其余所有房间都被锁住。你的目标是进入所有的房间。然而,你不能在没有获得钥匙的时候进入锁住的房间。
当你进入一个房间,你可能会在里面找到一套不同的钥匙,每把钥匙上都有对应的房间号,即表示钥匙可以打开的房间。你可以拿上所有钥匙去解锁其他房间。
给你一个数组 rooms 其中 rooms[i] 是你进入 i 号房间可以获得的钥匙集合。如果能进入 所有 房间返回 true,否则返回 false。
代码如下:
class Solution {
public:
bool canVisitAllRooms(vector>& rooms) {
int n = rooms.size();//行数
queue que;
for(int i=0;ivisit(n,false);
visit[0] = true;
while(!que.empty())
{
int t = que.front();
que.pop();
if(!visit[t])
{
visit[t]=true;
for(auto key:rooms[t])
{
que.push(key);
}
}
}
for(int i=0;i 547. 省份数量
有 n 个城市,其中一些彼此相连,另一些没有相连。如果城市 a 与城市 b 直接相连,且城市 b 与城市 c 直接相连,那么城市 a 与城市 c 间接相连。
省份 是一组直接或间接相连的城市,组内不含其他没有相连的城市。
给你一个 n x n 的矩阵 isConnected ,其中 isConnected[i][j] = 1 表示第 i 个城市和第 j 个城市直接相连,而 isConnected[i][j] = 0 表示二者不直接相连。
返回矩阵中省份的数量。
代码如下:
class Solution {
int f[205];
int find(int a)
{
if(f[a]!=a)
f[a]=find(f[a]);
return f[a];
}
void Uoion(int a,int b)
{
int aa=find(a);
int bb=find(b);
if(aa==bb) return;
f[bb]=aa;
}
public:
int findCircleNum(vector>& isConnected) {
for(int i=1;i<205;i++) f[i]=i;
int n=isConnected.size();
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
if(isConnected[i-1][j-1])
{
Uoion(i,j);
}
}
}
int cnt=0;
unordered_set_set;
for(int i=1;i<=n;i++)
{
int a=find(i);
if(!_set.count(a))
{
cnt++;
_set.insert(a);
}
}
return cnt;
}
}; 1466. 重新规划路线
n 座城市,从 0 到 n-1 编号,其间共有 n-1 条路线。因此,要想在两座不同城市之间旅行只有唯一一条路线可供选择(路线网形成一颗树)。去年,交通运输部决定重新规划路线,以改变交通拥堵的状况。
路线用 connections 表示,其中 connections[i] = [a, b] 表示从城市 a 到 b 的一条有向路线。
今年,城市 0 将会举办一场大型比赛,很多游客都想前往城市 0 。
请你帮助重新规划路线方向,使每个城市都可以访问城市 0 。返回需要变更方向的最小路线数。
题目数据 保证 每个城市在重新规划路线方向后都能到达城市 0 。
代码如下:
class Solution {
public:
int ans =0;
int minReorder(int n, vector>& connections)
{
auto g = buildGraph(n,connections);
dfs(0,-1,g);
return ans;
}
vector>> buildGraph(int n, vector>& connections)
{
vector>>ans(n);
for(auto c:connections)
{
ans[c[0]].push_back({c[1], true});
ans[c[1]].push_back({c[0], false});
}
return ans;
}
void dfs(int node,int parent,vector>>& g) //邻接表表示
{
for(auto c:g[node])
{
if(c.first!=parent)
{
if(c.second==true)
ans++;
dfs(c.first,node,g);
}
}
}
}; 399. 除法求值
给你一个变量对数组 equations 和一个实数值数组 values 作为已知条件,其中 equations[i] = [Ai, Bi] 和 values[i] 共同表示等式 Ai / Bi = values[i] 。每个 Ai 或 Bi 是一个表示单个变量的字符串。
另有一些以数组 queries 表示的问题,其中 queries[j] = [Cj, Dj] 表示第 j 个问题,请你根据已知条件找出 Cj / Dj = ? 的结果作为答案。
返回 所有问题的答案 。如果存在某个无法确定的答案,则用 -1.0 替代这个答案。如果问题中出现了给定的已知条件中没有出现的字符串,也需要用 -1.0 替代这个答案。
注意:输入总是有效的。你可以假设除法运算中不会出现除数为 0 的情况,且不存在任何矛盾的结果
代码如下:
class UnionFind
{
public:
pair find(const string& key)
{
auto it = parents.find(key);
if (it == parents.end())
return {"", 0};
if (it->second == key)
return {key, 1};
auto [p, w] = find(it->second);
parents[key] = p;
weights[key] *= w;
return {p, weights[key]};
}
UnionFind& add(const string& key)
{
if (!parents.count(key)) {
parents[key] = key;
weights[key] = 1;
}
return *this;
}
void merge(const string& k1, const string& k2, double value)
{
auto [pk1, w1] = find(k1);
auto [pk2, w2] = find(k2);
if (pk1 == pk2)
return;
weights[pk2] = w1 * value / w2;
parents[pk2] = pk1;
}
private:
unordered_map weights;
unordered_map parents;
};
class Solution {
public:
vector calcEquation(vector>& equations,
vector& values,
vector>& queries)
{
UnionFind uf;
for (int i = 0; i < equations.size(); ++i) {
string k1 = equations[i][0], k2 = equations[i][1];
uf.add(k1).add(k2).merge(k1, k2, values[i]);
}
vector result;
for (auto& eq : queries) {
string k1 = eq[0], k2 = eq[1];
auto [pk1, w1] = uf.find(k1);
auto [pk2, w2] = uf.find(k2);
if (pk1 == pk2 && !pk1.empty()) {
result.push_back(w2 / w1);
} else {
result.push_back(-1);
}
}
return result;
}
}; 图 - 广度优先搜索
1926. 迷宫中离入口最近的出口
你一个 m x n 的迷宫矩阵 maze (下标从 0 开始),矩阵中有空格子(用 '.' 表示)和墙(用 '+' 表示)。同时给你迷宫的入口 entrance ,用 entrance = [entrancerow, entrancecol] 表示你一开始所在格子的行和列。
每一步操作,你可以往 上,下,左 或者 右 移动一个格子。你不能进入墙所在的格子,你也不能离开迷宫。你的目标是找到离 entrance 最近 的出口。出口 的含义是 maze 边界 上的 空格子。entrance 格子 不算 出口。
请你返回从 entrance 到最近出口的最短路径的 步数 ,如果不存在这样的路径,请你返回 -1
代码如下:
class Solution {
public:
int nearestExit(vector>& maze, vector& entrance)
{
int dx[4] = {1, 0, 0, -1}, dy[4] = {0, 1, -1, 0};
int sx = entrance[0], sy = entrance[1];
int m = maze.size(), n = maze[0].size();
queue> que;
que.push({sx, sy});
maze[sx][sy] = '+';
int step = 0;
while(!que.empty())
{
int size = que.size();
while(size--)
{
auto [x, y] = que.front();
que.pop();
for(int i = 0; i < 4; i++)
{
int nx = x + dx[i], ny = y + dy[i]; //只能往一个方向移动,而不是歇着运动
if(nx >= 0 && nx < m && ny >= 0 && ny < n)
{
if(maze[nx][ny] == '.')
{
if(nx == 0 || nx == m - 1 || ny == 0 || ny == n - 1)
return step + 1;
else
{
que.push({nx, ny});
maze[nx][ny] = '+';
}
}
}
}
}
step++;
}
return -1;
}
}; 994. 腐烂的橘子
在给定的 m x n 网格 grid 中,每个单元格可以有以下三个值之一:
值 0 代表空单元格;
值 1 代表新鲜橘子;
值 2 代表腐烂的橘子。
每分钟,腐烂的橘子 周围 4 个方向上相邻 的新鲜橘子都会腐烂。
返回 直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能,返回 -1 。
代码如下:
class Solution {
public:
int orangesRotting(vector>& grid)
{
int n_row = grid.size();//行数
int n_col = grid[0].size();//列数
queue>que;
int count = 0;
for(int i=0;i=0 && grid[i-1][j] == 1)
{ //上面存在
grid[i-1][j] = 2;
que.push(make_pair(i-1,j));
flag =1;
}
if(i+1=0 && grid[i][j-1]==1)
{ //左边存在
grid[i][j-1] = 2;
que.push(make_pair(i,j-1));
flag=1;
}
if(j+1 堆 / 优先队列
215. 数组中的第K个最大元素
给定整数数组 nums 和整数 k,请返回数组中第 k 个最大的元素。
请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。
你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。
示例代码1:
class Solution {
public:
int findKthLargest(vector& nums, int k) {
// 1、调用库函数sort()
sort(nums.begin(), nums.end());
return nums[nums.size() - k];
} 示例代码2:
class Solution {
public:
//2、快速排序
int quick_sort(vector& nums, int l, int r, int k) {
if(l == r) return nums[l];
int i,j,x;
i = l - 1;
j = r + 1;
x = nums[ (i + j) >> 1];
while(i < j){
do
{
j--;
} while(nums[j] < x);
do
{
i++;
} while(nums[i] > x);
if(i < j) swap(nums[i],nums[j]);
}
int ll = j - l + 1;
if(ll >= k) return quick_sort(nums,l,j,k);
return quick_sort(nums,j + 1, r, k - ll);
}
int findKthLargest(vector& nums, int k) {
return quick_sort(nums,0,nums.size() - 1,k);
}
}; 2336. 无限集中的最小数字
现有一个包含所有正整数的集合 [1, 2, 3, 4, 5, ...] 。
实现 SmallestInfiniteSet 类:
SmallestInfiniteSet() 初始化 SmallestInfiniteSet 对象以包含 所有 正整数。
int popSmallest() 移除 并返回该无限集中的最小整数。
void addBack(int num) 如果正整数 num 不 存在于无限集中,则将一个 num 添加 到该无限集中。
代码如下:
class SmallestInfiniteSet {
public:
priority_queue, greater> added;
unordered_set added_set;
int min = 1;
SmallestInfiniteSet() {
}
int popSmallest() {
if(added_set.empty()) return min++;
int res = added.top(); added.pop();
added_set.erase(added_set.find(res));
return res;
}
void addBack(int num) {
if(num < min && added_set.find(num)==added_set.end())
{
added_set.emplace(num);
added.push(num);
}
}
};
/**
* Your SmallestInfiniteSet object will be instantiated and called as such:
* SmallestInfiniteSet* obj = new SmallestInfiniteSet();
* int param_1 = obj->popSmallest();
* obj->addBack(num);
*/ 2542. 最大子序列的分数
给你两个下标从 0 开始的整数数组 nums1 和 nums2 ,两者长度都是 n ,再给你一个正整数 k 。你必须从 nums1 中选一个长度为 k 的 子序列 对应的下标。
对于选择的下标 i0 ,i1 ,..., ik - 1 ,你的 分数 定义如下:
nums1 中下标对应元素求和,乘以 nums2 中下标对应元素的 最小值 。
用公示表示: (nums1[i0] + nums1[i1] +...+ nums1[ik - 1]) * min(nums2[i0] , nums2[i1], ... ,nums2[ik - 1]) 。
请你返回 最大 可能的分数。
一个数组的 子序列 下标是集合 {0, 1, ..., n-1} 中删除若干元素得到的剩余集合,也可以不删除任何元素。
代码如下:
static const int _ = []() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
return 0;
}();
class Solution {
public:
long long maxScore(vector& nums1, vector& nums2, int k)
{
long long sum{};
long long mnx{100000L};
long long res{};
vector> nums{};
priority_queue, std::greater> pq{};
for(int i = 0; i < nums1.size(); ++i) {
nums.push_back({nums1[i],nums2[i]});
}
sort(nums.begin(), nums.end(),[](auto& lhs, auto& rhs) {
return lhs.second > rhs.second;
});
for(int i = 0; i < nums.size(); ++i)
{
#define n1 nums[i].first
#define n2 nums[i].second
if(i < k) {
pq.push(n1);
sum += n1;
mnx = n2;
}
else {
res = max(res, sum*mnx);
if(n1 > pq.top()) {
sum = sum - pq.top() + n1;
pq.push(n1);
pq.pop();
}
mnx = n2;
}
}
return max(res,sum*mnx);
}
}; 2462. 雇佣 K 位工人的总代价
给你一个下标从 0 开始的整数数组 costs ,其中 costs[i] 是雇佣第 i 位工人的代价。
同时给你两个整数 k 和 candidates 。我们想根据以下规则恰好雇佣 k 位工人:
总共进行 k 轮雇佣,且每一轮恰好雇佣一位工人。
在每一轮雇佣中,从最前面 candidates 和最后面 candidates 人中选出代价最小的一位工人,如果有多位代价相同且最小的工人,选择下标更小的一位工人。
比方说,costs = [3,2,7,7,1,2] 且 candidates = 2 ,第一轮雇佣中,我们选择第 4 位工人,因为他的代价最小 [3,2,7,7,1,2] 。
第二轮雇佣,我们选择第 1 位工人,因为他们的代价与第 4 位工人一样都是最小代价,而且下标更小,[3,2,7,7,2] 。注意每一轮雇佣后,剩余工人的下标可能会发生变化。
如果剩余员工数目不足 candidates 人,那么下一轮雇佣他们中代价最小的一人,如果有多位代价相同且最小的工人,选择下标更小的一位工人。
一位工人只能被选择一次。
返回雇佣恰好 k 位工人的总代价。
代码如下:
class Solution {
public:
long long totalCost(vector& costs, int k, int candidates) {
priority_queue,greater> q1,q2;
long long ans=0;
int i=0;
int j=costs.size()-1;
while(k--){
while(q1.size() 二分查找
374. 猜数字大小
猜数字游戏的规则如下:
每轮游戏,我都会从 1 到 n 随机选择一个数字。 请你猜选出的是哪个数字。
如果你猜错了,我会告诉你,你猜测的数字比我选出的数字是大了还是小了。
你可以通过调用一个预先定义好的接口 int guess(int num) 来获取猜测结果,返回值一共有 3 种可能的情况(-1,1 或 0):
-1:我选出的数字比你猜的数字小 pick < num
1:我选出的数字比你猜的数字大 pick > num
0:我选出的数字和你猜的数字一样。恭喜!你猜对了!pick == num
返回我选出的数字。
代码如下:
/**
* Forward declaration of guess API.
* @param num your guess
* @return -1 if num is higher than the picked number
* 1 if num is lower than the picked number
* otherwise return 0
* int guess(int num);
*/
class Solution {
public:
int guessNumber(int n) {
int left = 1, right = n;
while (left < right) { // 循环直至区间左右端点相同
int mid = left + (right - left) / 2; // 防止计算时溢出
if (guess(mid) <= 0) {
right = mid; // 答案在区间 [left, mid] 中
} else {
left = mid + 1; // 答案在区间 [mid+1, right] 中
}
}
// 此时有 left == right,区间缩为一个点,即为答案
return left;
}
};2300. 咒语和药水的成功对数
给你两个正整数数组 spells 和 potions ,长度分别为 n 和 m ,其中 spells[i] 表示第 i 个咒语的能量强度,potions[j] 表示第 j 瓶药水的能量强度。
同时给你一个整数 success 。一个咒语和药水的能量强度 相乘 如果 大于等于 success ,那么它们视为一对 成功 的组合。
请你返回一个长度为 n 的整数数组 pairs,其中 pairs[i] 是能跟第 i 个咒语成功组合的 药水 数目。
代码如下:
class Solution {
public:
int binarySearch(int spell, vector& potions, long long success) {
int left = 0, right = potions.size() - 1;
while(left < right)
{
int mid = left + (right - left) / 2;
if((long long)spell * (long long)potions[mid] >= success)
{
right = mid;
}
else
{
left = mid + 1;
}
}
if((long long)spell * (long long)potions[left] >= success) left--;
return potions.size() - left - 1;
}
vector successfulPairs(vector& spells, vector& potions, long long success) {
sort(potions.begin(), potions.end());
vector pairs(spells.size());
for(int i = 0; i < pairs.size(); ++i)
{
pairs[i] = binarySearch(spells[i], potions, success);
}
return pairs;
}
}; 162. 寻找峰值
峰值元素是指其值严格大于左右相邻值的元素。
给你一个整数数组 nums,找到峰值元素并返回其索引。数组可能包含多个峰值,在这种情况下,返回 任何一个峰值 所在位置即可。
你可以假设 nums[-1] = nums[n] = -∞ 。
你必须实现时间复杂度为 O(log n) 的算法来解决此问题。
代码如下:
class Solution {
public:
int findPeakElement(vector& nums) {
if(nums.size()<2){
return 0;
}
int left = 0,right = nums.size()-1;
int mid;
while(left < right){
mid = left+(right-left)/2;
if(nums[mid] 875. 爱吃香蕉的珂珂
珂珂喜欢吃香蕉。这里有 n 堆香蕉,第 i 堆中有 piles[i] 根香蕉。警卫已经离开了,将在 h 小时后回来。
珂珂可以决定她吃香蕉的速度 k (单位:根/小时)。每个小时,她将会选择一堆香蕉,从中吃掉 k 根。如果这堆香蕉少于 k 根,她将吃掉这堆的所有香蕉,然后这一小时内不会再吃更多的香蕉。
珂珂喜欢慢慢吃,但仍然想在警卫回来前吃掉所有的香蕉。
返回她可以在 h 小时内吃掉所有香蕉的最小速度 k(k 为整数)。
代码如下:
class Solution {
public:
int minEatingSpeed(vector& piles, int h) {
int l = 1;
int r = *max_element(piles.begin(), piles.end());
auto check = [&](int mid)
{
int t = 0;
for(auto &p : piles)
{
t += p / mid + (p % mid != 0);
}
return t <= h;
};
while(l < r)
{
int mid = (l + r) / 2;
(check(mid) ? (r = mid) : (l = mid + 1));
}
return r;
}
};