链表经典OJ题（链表回文结构，链表带环，链表的深拷贝）

目录

前言

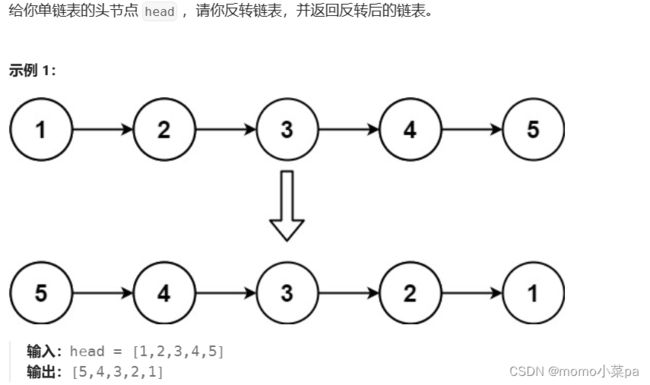
1.反转一个单链表。 

2.   给定一个带有头结点 head 的非空单链表，返回链表的中间结点。

3.链表的回文结构。

 4.链表带环问题（*****）

4.1是否带环

4.2 入环的节点

5.随机链表的复制（链表的深拷贝）

---

前言

        前面我们学习了链表，现在我们来手撕几道经典链表OJ题目吧！！！

---

1.反转一个单链表。 

题目链接206. 反转链表 - 力扣（LeetCode）

题解：

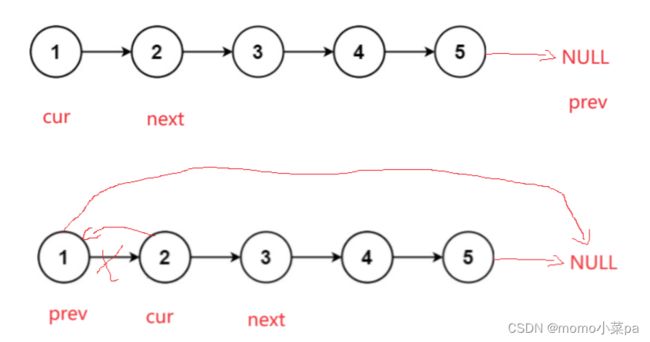
        在这一题，我们定义了三个指针变量，首先让prev指向NULL，prev的作用是保存cur的前面的一个节点，next是保存cur后面的节点。

        每一次循环迭代，都让cur指向前面的节点，也就是指向prev；

        再让prev去到cur的位置，cur去到next位置，最后再让next去到cur->next的位置，这样就完成了一次循环迭代。直到cur为NULL；
 

struct ListNode* reverseList(struct ListNode* head) {
    struct ListNode*prev = NULL;
    struct ListNode*cur = head;
    struct ListNode*next =head;
    while(cur)
    {
        next = cur->next;
        cur->next = prev;
        prev =cur;
        cur = next;
    }
    return prev;
}

        这样就通过了！

      

---

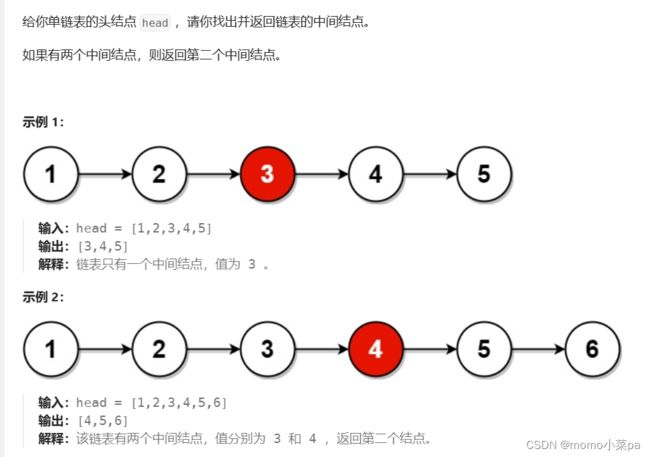
2.   给定一个带有头结点 head 的非空单链表，返回链表的中间结点。

题目链接：876. 链表的中间结点 - 力扣（LeetCode）

 

题解：​

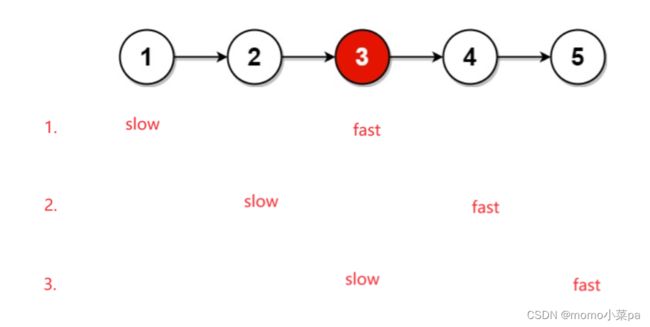
        这题思想其实非常简单，既然让返回中间节点，那么我们就定义两个指针，fast和slow，让fast走两步，slow走一步，这样fast走完全程之后，slow就只走了一半。

        需要注意的是，节点总数为奇数时，fast走到最后一个节点就结束，而节点总数为偶数时，fast节点就要走到NULL。因此结束条件就要写成（fast&&fast->next）。

struct ListNode* middleNode(struct ListNode* head){
    struct ListNode* slow = head,*fast = head;
    while(fast&&fast->next)
    {
        slow = slow->next;
        fast = fast->next->next;
    }

    return slow;
}

---

3.链表的回文结构。

题目链接：链表的回文结构_牛客题霸_牛客网 (nowcoder.com)

​
 题解：​

        这一题看似复杂，实际不难。我们只需要找到中间节点，然后从中间节点反转链表 ，再分别从两个头开始遍历，若每个节点都相等，则为回文结构。

        如果是奇数个，两条链表节点数量会不会不想等呢？

        不会！因为A链表的最后一个并没有与B链表的最后一个节点断开，所以两链表有一个 公共节点，因此在奇数个节点下，两链表节点个数也相同，结束条件显而易见为：（head&&rhead）。

class PalindromeList {
public:
struct ListNode* reverseList(struct ListNode* head) {//反转链表
    struct ListNode*prv = NULL;
    struct ListNode*cur = head;
    struct ListNode*n =head;
    while(n)
    {
        n = cur->next;
        cur->next = prv;
        prv =cur;
        cur = n;
    }
    return prv;
}
struct ListNode* middleNode(struct ListNode* head){//找中间节点
    struct ListNode* slow = head,*fast = head;
    while(fast&&fast->next)
    {
        slow = slow->next;
        fast = fast->next->next;
    }

    return slow;
}
    bool chkPalindrome(ListNode* A) {
        ListNode* mid = middleNode(A);
        ListNode*rhead = reverseList(mid);
        while(A&&rhead)
        {
            if(A->val!=rhead->val)
                return false;
            A=A->next;
            rhead=rhead->next;
        }
        return true;
    }    
};

---

 4.链表带环问题（*****）

        链表带环问题是链表中非常重要的一类问题，在企业面试中也会经常遇到。此类问题有两种，第一种是判断链表是否带环，第二种是判断链表开始入环的节点是哪个。

---

4.1是否带环

题目链接：141. 环形链表 - 力扣（LeetCode）

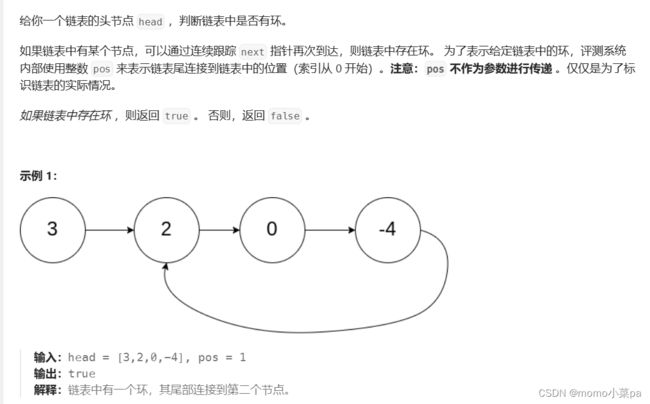
题解：我们不禁思索，该如何判断链表是否带环呢？

        在这里我们可以定义两个指针fast和slow，让fast先走，如果到最后还能与slow相遇，那就证明该链表是带环的。在此就引出了一个问题，fast要比slow快多少？

        1.slow一次走一步fast一次走两步一定会相遇吗？

        答案是一定会相遇，因为fast和slow的距离每次都缩减1，到最后一定会减到0。

        2.slow一次走一步fast一次走三步一定会相遇吗？

        答案是不一定，如果N为偶数，fast和slow的距离每次都缩减2，最后一定会减到0。如果为奇数，最后会减到-1，这样就又开始新一轮的追击了，而且永远不会相遇。

        3.slow一次走n步fast一次走m步一定会相遇吗？（m>n>1）

        最后我们得到2L = n*C-N最后一定得到的是一个奇数，所以最后一定能追上。

bool hasCycle(struct ListNode *head) {
    struct ListNode* fast = head,*slow =head;
    while(fast&&fast->next)
    {
        fast =fast->next->next;
        slow =slow ->next;
        if(fast ==slow)
            return fast;
    }
    return NULL;
}

---

4.2 入环的节点

题目链接：142. 环形链表 II - 力扣（LeetCode） 、

题解：这一题与上一题是不一样的，这一题是要找到入环的节点，从哪个节点开始入环，这题难度相较于上一题显然是上升了。

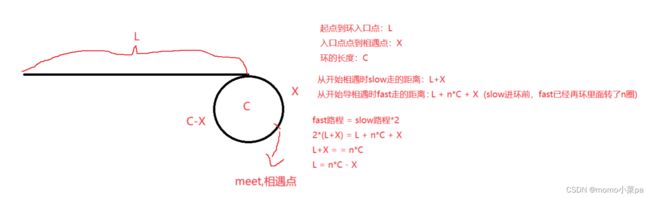
        假设，fast和slow在meet点相遇，那么slow就走了（L+X）的距离，fast就走了（L+X+n*C）的距离，最后由图上等式可得，L=n*C-X，那也就是说，如果相同速度的指针，一个从相遇点开始走，另一个从入口点开始走，他们到入口与点的距离是一样的，所以一定会在入口点相遇。

        因此本题思路就出来了：1.找到相遇点 2.让相同速度的指针，一个从相遇点开始走，另一个从入口点开始走。最终就一定会相遇。

struct ListNode *detectCycle(struct ListNode *head) {
    struct ListNode *slow = head,*fast =head;
    while(fast&&fast->next)
    {
        slow = slow->next;
        fast= fast->next->next;
        if(slow == fast)
        {
            struct ListNode* meet= slow;
            while(head!=meet)
            {
                head = head->next;
                meet =meet->next;

            }
            return meet;
        }
    }
    return NULL;
}

---

5.随机链表的复制（链表的深拷贝）

题目链接：138. 随机链表的复制 - 力扣（LeetCode）

题解：链表的深拷贝，是链表中较难的问题，但如果把思路理清，问题也就迎刃而解了。

        我们的第一思路可能就是将每个节点的信息先拷贝下来，然后我们来处理random的指向的时候，可能就是用嵌套循环将每个节点的random进行比较，来确定指向，这样一来就造成时间复杂度到达O(N^2)了，这就不符合题目要求了。

        那么我这里就提供一种可行的思路：

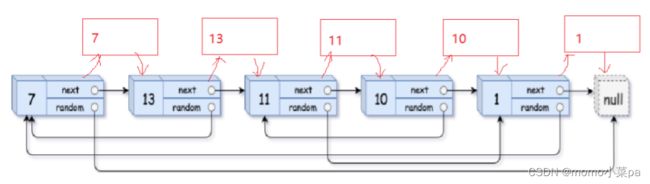
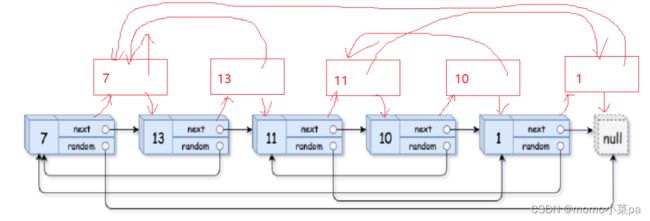
                1.拷贝的节点都插入在原来节点的后面（如图）

                2.处理random的指向

        我们可以清楚的看到，原节点的下一个节点就是我们所拷贝的节点，那么让本来指向原节点random，指向原节点的下一个是不是就可以让拷贝节点的random完成正确的指向，这就解决了然random指向的问题了。如图（我们已经得到所有的拷贝节点了。）

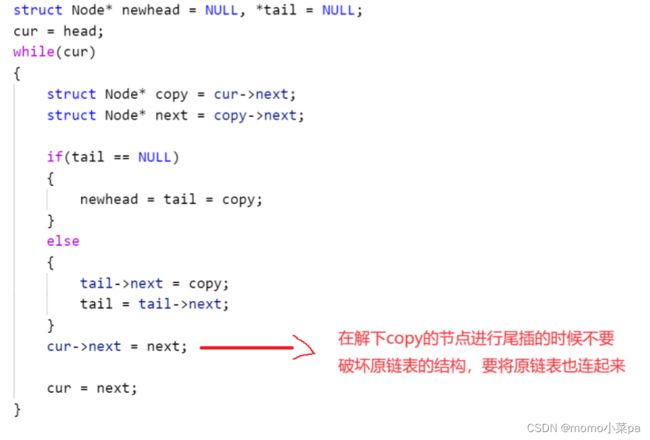
                3.copy的节点一个一个的解下来尾插就可以得到我们想要的深拷贝出来的链表了。

完整代码：

truct Node* copyRandomList(struct Node* head) {
	struct Node* cur =head;
    while(cur)
    {
        struct Node*copy= (struct Node*)malloc(sizeof(struct Node));
        copy->val =cur->val;
        copy->next = cur->next;
        cur->next = copy;
        cur=cur->next->next;
    }
    cur =head;
    while(cur)
    {
        struct Node*copy= cur->next;
        if(cur->random ==NULL)
            copy->random =NULL;
        else
            copy->random = cur->random->next;
        cur = cur->next->next; 
    }
    struct Node* newhead = NULL,*fail=NULL;
    cur =head;
    while(cur)
    {
        struct Node*copy = cur->next;
        struct Node*next =copy->next;
        if(newhead==NULL)
        {
            newhead = fail = copy;
        }
        else
        {
            fail->next = copy;
            fail=fail->next;
        }
            
        cur->next = next;
        cur = next;
    }
    return newhead;
}

这里都是链表比较经典的题目，希望对你有所帮助！！！