数据分析实战 | 泊松回归——航班数据分析

目录

一、数据及分析对象

二、目的及分析任务

三、方法及工具

四、数据读入

五、数据理解

六、数据准备

七、模型训练

八、模型评价

---

一、数据及分析对象

CSV文件：o-ring-erosion-only.csv

数据集链接：https://download.csdn.net/download/m0_70452407/88524654

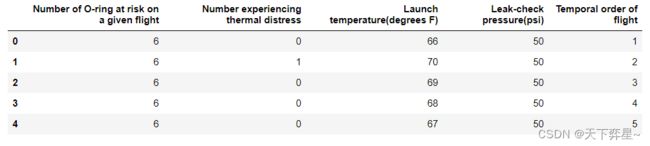
该数据集给出了挑战者航天飞机的O型圈（O-Ring）数据，主要属性如下：

（1）Number of O-ring at risk on a given flight：航班上存在潜在风险的O形环数量。

（2）Number experiencing thermal distress：出现热损伤的O形环数量。

（3）Launch temperature(degrees F)：发射温度（华氏度）。

（4）Leak-check pressure(psi)：捡漏压力（psi）。

（5）Temporal order of flight：航班时序。

二、目的及分析任务

理解机器学习方法在数据分析中的应用——采用泊松回归方法进行回归分析。

（1）以全部记录为训练集进行泊松回归建模。

（2）对模型进行假设检验和可视化处理，验证泊松回归建模的有效性。

三、方法及工具

Python语言及其第三方包pandas、NumPy和statsmodels

四、数据读入

由于原数据没有表头，因此在读取CSV文件时通过names参数手动生成表头。

import pandas as pd
df_erosion=pd.read_csv("D:\\Download\\JDK\\数据分析理论与实践by朝乐门_机械工业出版社\\第3章 回归分析\\o-ring-erosion-only.csv",
                      names=['Number of O-ring at risk on a given flight','Number experiencing thermal distress',
                            'Launch temperature(degrees F)','Leak-check pressure(psi)','Temporal order of flight'])

df_erosion.head()

五、数据理解

对数据框df_erosion进行探索性分析：

df_erosion.describe()

其中，预测变量"Number experiencing thermal distress"的最大值为2，最小值为0，平均热损伤O形环数为0.391。

除了describe()方法，还可以调用shape属性和columns属性对数据框进行探索性分析。

df_erosion.shape

(23, 5)

df_erosion.columns

Index(['Number of O-ring at risk on a given flight',
       'Number experiencing thermal distress', 'Launch temperature(degrees F)',
       'Leak-check pressure(psi)', 'Temporal order of flight'],
      dtype='object')

绘制直方图来查看因变量“Number experiencing thermal distress”数据的连续性，通过调用mayplotlib.pyplot包中数据框（DataFrame）的hist()方法创建频数直方图。

import matplotlib.pyplot as plt
plt.rcParams['font.family']="simHei"   #汉字显示 字体设置
plt.hist(df_erosion['Number experiencing thermal distress'],
        bins=10,
        facecolor="blue",
        edgecolor="black",
        alpha=0.7)
plt.xlabel('区间')
plt.ylabel('频数')
plt.title("因变量‘Number experiencing thermal distress’频数分布直方图")

通过调用NumPy包中数据框（DataFrame)的mean()方法和var()方法查看因变量“Number experiencing thermal distress”的均值和方差。

import numpy as np
print(np.mean(df_erosion['Number experiencing thermal distress']))
print(np.var(df_erosion['Number experiencing thermal distress']))

0.391304347826087
0.41209829867674863

可以看到方差约等于平均值，避免了在泊松分布中发生过度分散或分散不足的情况。泊松分布的一个重要特征是均值和方差相等，称为分散均衡。只有分散均衡的数据才能使用泊松分布模型。均值小于方差称为分散过度，所有分布向左侧倾斜，数值较小的数据出现概率较高。均值大于方差的称为分散不足。

六、数据准备

进行泊松回归分析前，应准备好模型所需的特征矩阵（X）和目标向量（y）。这里采用Python的统计分析包statsmodels进行自动你类型转换，数据对象y即可使用。若采用其他包（如scikit-learn等需要采用np.ravel()方法对y进行转换）。

原始数据集中列名过长，需要对其重新命名。同时遵从习惯调整特征顺序，将因变量调至最后一列。

df_erosion.rename(columns={'Number of O-ring at risk on a given flight':'num_rings',
                          'Launch temperature(degrees F)':'temperature',
                          'Leak-check pressure(psi)':'pressure',
                          'Number experiencing thermal distress':'num_distress',
                          'Temporal order of flight':'order'},inplace=True)
order=['num_rings','temperature','pressure','order','num_distress']
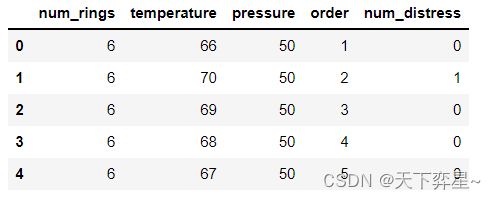
df_erosion=df_erosion[order]

df_erosion.head()

七、模型训练

以航班上存在潜在风险的O形环数量num_rings、发射温度temperature、捡漏压力pressure和航班时许order作为自变量，飞行中热损伤O形环的数量num_distress作为因变量对数据进行泊松回归建模。这里采用的实现方式为调用Python的统计分析包statsmodels中的GLM()方法进行建模分析。

import statsmodels.formula.api as smf

statsmodels.GLM()方法的输入有3个，第一个形参为formula,具体形式为y~x,在这里即为“num_distress~num_rings+temperature+pressure+order"。第二个参数是模型训练所用的数据集df_erosion。最后一个参数为创建GLM模型所用的Poisson()模型。这里通过调用NumPy库的column_stack()方法对各自变量矩阵按列合并创建特征矩阵X。

x=np.column_stack((df_erosion['num_rings'],df_erosion['temperature']
                   ,df_erosion['pressure'],df_erosion['order']))

在自变量x和因变量y上使用GLM()方法进行泊松回归。

import statsmodels.api as sm
glm=smf.glm('num_distress~num_rings+temperature+pressure+order'
            ,df_erosion,family=sm.families.Poisson())

然后获取拟合结果，并将回归拟合的摘要全部打印出来。

results=glm.fit()
print(results.summary())

   Generalized Linear Model Regression Results                  
==============================================================================
Dep. Variable:           num_distress   No. Observations:                   23
Model:                            GLM   Df Residuals:                       19
Model Family:                 Poisson   Df Model:                            3
Link Function:                    Log   Scale:                          1.0000
Method:                          IRLS   Log-Likelihood:                -15.317
Date:                Sat, 11 Nov 2023   Deviance:                       15.407
Time:                        12:45:43   Pearson chi2:                     23.4
No. Iterations:                     5   Pseudo R-squ. (CS):             0.2633
Covariance Type:            nonrobust                                         
===============================================================================
                  coef    std err          z      P>|z|      [0.025      0.975]
-------------------------------------------------------------------------------
Intercept       0.0984      0.090      1.094      0.274      -0.078       0.275
num_rings       0.5905      0.540      1.094      0.274      -0.468       1.649
temperature    -0.0883      0.042     -2.092      0.036      -0.171      -0.006
pressure        0.0070      0.010      0.708      0.479      -0.012       0.026
order           0.0115      0.077      0.150      0.881      -0.138       0.161
===============================================================================

第二部分的coef列所对应的Intercept、num_rings、temperature、pressure和order就是计算出的回归模型中各自变量的系数。

除了读取回归摘要外，还可以调用params属性查看拟合结果。

results.params

Intercept      0.098418
num_rings      0.590510
temperature   -0.088329
pressure       0.007007
order          0.011480
dtype: float64

八、模型评价

通过模型摘要可以看到，只有自变量temperature的p值小于0.05，通过了T检验。这意味着其他解释变量在控制temperature的前提下，对因变量的影响不显著。

建立的泊松回归模型如下：

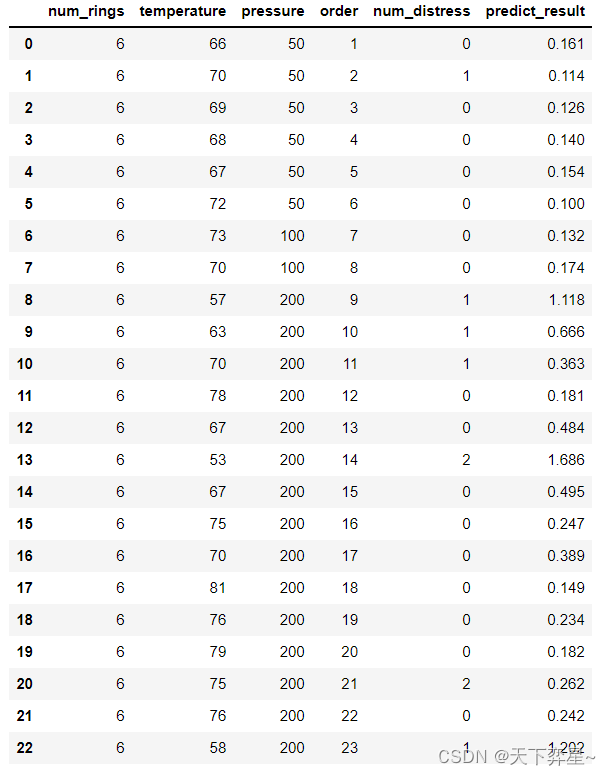
模型的预测结果如下：

df_erosion['predict_result']=results.predict(df_erosion)
df_erosion['predict_result']=df_erosion['predict_result'].apply(lambda x:round(x,3))

df_erosion

最后采用均方根误差（RMSE）来评估模型预测结果。

from sklearn.metrics import mean_squared_error
print("RMSE:",np.sqrt(mean_squared_error(df_erosion.predict_result,df_erosion.num_distress)))

RMSE: 0.4895481057323038

 此结果说明该模型的均方根误差为0.490，表明该模型有一定的预测能力。