MIT算法导论（一）——算法分析和引论

1 算法分析及引论

1.1 算法

算法是一门关注性能的学科，也就是说，我们致力于让我们要做的事变得更快。让我们提出一个问题，在程序设计中，什么比性能更重要？

成本（程序员的时间成本），可维护性，稳定性（健壮性，是否老崩溃），功能性，安全，可扩展性。

既然这么多因素都比性能更重要，那我们为何还要研究算法，到底是性能重要还是用户的体验更重要呢？

可以肯定的是，很多时候性能和用户体验是紧密联系在一起的，很多时候没有什么东西比干等着更难受了。

我们研究算法的缘由是：很多时候性能的好坏决定其是否可行，如我们对实时的要求，如果算法性能不快，那么就会导致无法追求实时的效果，实时当然就不可行了。或者说，如果它占用过多的内存，它也是不可行的，因为硬件需求跟不上。总的来说：算法走在所有因素的最前沿

第二个关键是，算法是一种解释性语言。其通用让几乎所有程序员都接收，它是一种让程序最为简洁的思考方式。我们有一个很好说明的例子：我们把算法比作货币，那么货币作为社会最底层的东西，如果你想要买吃的，买住的，都离不开货币。

第三个关键是，算法决定了一个程序的安全和用户体验的好坏。虽然C比Java快很多，java编程性能会损失三倍左右，但是人们还是喜欢用java来编写程序，因为java的面向对象机制以及异常机制值得人们为之付出。这也是为什么我们要提高性能，因为我们总是把性能分摊给其他的要素。

第四个关键是，我们对此乐此不疲。人们总是喜欢快的东西，比如火箭、滑雪，我们总喜欢这些快速的东西。

在某种意义上，上述这些简单的问题是我们研究下列问题的指路明灯。

1.2 排序

让我们来看看一个非常古老的问题，排序。排序包含了许多基本的算法。让我们举一个排序的例子：我们输入一组序列$a_1,a_2...a_n$，按照需求排列后作为输出。排列一般是使得如$a_1<=a_2...<=a_n$一般。按一定顺序排序。

1.2.1 插入排序

1.2.1.1 插入排序原理

这里我们介绍第一个算法，即插入排序。通常我们描述算法用的是伪代码而不是编程语言。伪代码中包含有一些解释性语言如英语或者中文，其能够让我们更清楚该算法包含的思想。

值得一提的是，用伪代码描述算法时，我们通常会使用缩进，其相当于大多数语言中标注开始和结束的分隔符。好比Java和C中的大括号。事实上，历史上还真有一些语言（例如python）是用缩进代表分隔，但是不是一种好的主义，因为在换页的时候，你很难知道自己在哪一个嵌套的层级，而是用大括号就能够很好的表示。

让我们缔造一个数组，如下所示：

这个数组通常是无序的，然而我们通过从从左到右指定一个变量，这个变量我们称为键，他会从数组中提取数据，然后和前面已经排好的序列做比较，然后插入前面的序列，这也是为这么这个算法叫做插入排序的原因。

比较经典的例子我认为是斗地主，在发牌时，我们时常会事先排好手中的牌，我们是一张一张拿起来的，然后将乱序的牌提取出来，然后插入前面已经排序好的位置中。无论什么时候，左手的牌都是排好序的，而右手拿的牌都是即将要插入到排好序的牌中，并且插入位置符合其自身顺序。

我们来看一下插入排序的伪代码实现：

INSERTION-SORT(A)
	for j←2 to length[A]
		do key←A[j]
			Insert A[j] into the sorted sequence A[1..j-1]
			i←j-1
			while i>0 and A[i]>key
				do A[i+1]←A[i]
					i←i-1
				A[i+1]←key

看上面的伪代码似乎有些费劲，可事实上，它与我们上面讲述的别无二致。让我们引入一个具体的例子来体会这个算法。

我们有一个序列：8 2 4 9 3 6

当我们执行插入排序时，我们的首要任务是从第二个元素开始，依次提取键key，然后和前面排序好的序列做对比再插入。题意来看首先提取的是2，然后插入8之前。原序列则变为2 8 4 9 3 6。接着我们找到4，4和2 8进行比对，然后插入2和8之间，原序列变为2 4 8 9 3 6，以此类推按照排序规则循环移动。

让我们借助数学工具来解剖该算法。如果输入序列之前就有序，那么已排序序列后的排序工作量就大大减少。因为每次遍历，它都是做上面循环往复的事。最坏的情况是该序列刚好是逆序，那么每个元素都将进行插入排序。

对应在这道题上，这个例子总共有6个数据，我们将其输入的规模扩大到100000，那么一旦发生逆序，其时间开销很大。为此在进行算法分析时，我们通常使用渐进时间复杂度，即假设输入的规模为n，趋于无限，则运行时间可以看做是以n为映射的函数。

1.2.1.2 时间复杂度

上述引入的时间复杂度中，显然有最好最坏的情况，最坏对应算法时间的上限，其代表着对用户的一种承诺，（是的尊贵的用户我的程序是不会超过这个时间的）。而最好的情况对应着算法时间的下限。我们通常关注算法的最坏时间复杂度。即我们要给出用户保证，我们的程序总能做到这样，而不是有时能这样，我们通常会把输入考虑成最坏的情况，对应上面插入排序的例子，我们最坏的情况是逆序。

当然有时我们也会讨论平均时间复杂度，这个时候T(n)就成了我们算法的时间期望值。那不禁有人会问，期望值是啥？

我们希望听到一些比较数学味道的回答，所谓的期望实际上就是每种输入的运行时间，乘以那种输入出现的概率。这是一种连续型的思考方式，我们可以理解为加权平均。

那我们如何知道特定输入在给定情况下的概率是多少？有时候我们并不知道，所以我们需要给出一个假设了，一个有关输入的统计分布的假设，否则期望时间无从谈起。

最常见的假设是均匀分布，即所有规模为n的输入情况都是等可能地出现。

最后我们想讲讲最好时间复杂度，我们称之为假象！~bogus（我在大声地笑哈哈），没啥用！因为最好的情况不可能出现。如果一个序列已经排好序，我们还有必要去排序吗，哈哈哈。除非你想要cheat！欺骗！在你得到一个特定输入下，然后你得到一个比较满意的结果后欺骗自己，对！这就是我想要的效果，那你就可以考虑它。

1.2.1.3 渐进时间复杂度

回到这个算法，我们不禁发问，插入排序的最坏情况时间是多少？

最简单的回答是，这取决于你的计算机。你用的是超级计算机还是腕表那么大的计算机，算力会大相径庭。但是通常来说，我们都是比对两个算法在同一台机器上的表现，即相对速度。当然也有人关注绝对速度，我们猜想真有某种算法能无论在什么机器上运行都表现得更好吗？

以上的回答实际上会对我们最开始的问题造成混淆，这不得不提到我们的大局观（big idea）了，这也是为什么算法涉猎如此广泛的原因。我们应该使用抽象的眼光来看待事物，从复杂的情况中提取关键的因素对其分析。这就是所谓的渐进分析。渐进分析的基本思路是：忽略掉依赖于机器的常量，不去检查其因素，而是关注算法本身时间的增长。

使用渐进分析，自然要引入相应的数学符号。这里我们使用的是theta$\Theta$来表示渐进时间复杂度。实际上theta写起来很简单，你需要做的是，弃去它的低阶项，并忽略前面的常数因子。

比如一个算法花费时间是：$3n^3+90n^2-5n+6046$，那我们就要使用高数中采取的抓大头准则，使的$3n^3$后面的项全部抛弃，然后再把3抛弃掉即可。所得为$\Theta (n^3)$。

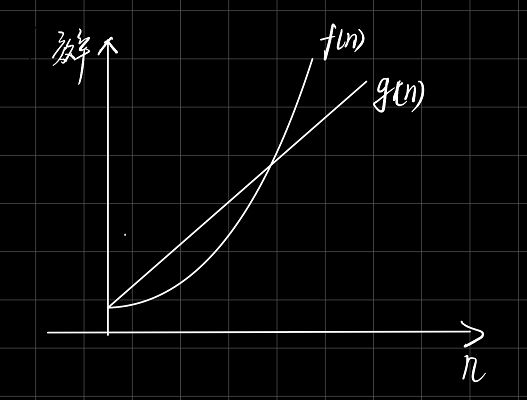
上述情况需要知道的是，假设有一个算法的时间复杂度是$\Theta (n^2)$，那么它迟早比$\Theta (n^3)$速度要快。因为当n逐渐增大时，指数会造成指数爆炸，使得比最大项还小的常数项无法动摇这个最终的结果。这对应到计算机的优劣上，即使你的$\Theta (n^2)$算法是在慢速计算机上运行，总有一天它也会超越在快速计算机上运行的$\Theta (n^3)$算法。

当然，站在工程角度上看，n有时候太大没有节制是不行的，这会导致我们的计算机无法运行该算法，这也是为什么有时候我们对一些慢速算法比较感兴趣，因为它们在n较少的时候能够保持较高的速度。所以仅仅会做算法分析并不能使你成为高手，你需要保持每天编程，并且在实际编程中运用，知道其什么时候相关什么时候不相关。

1.2.1.4 回到算法

这时候我们可以来分析一些刚才的插入排序算法了。就像我们说的我们关注其最坏时间复杂度。即输入为逆序。

INSERTION-SORT(A)
	for j←2 to length[A]
		do key←A[j]
			Insert A[j] into the sorted sequence A[1..j-1]
			i←j-1
			while i>0 and A[i]>key
				do A[i+1]←A[i]
					i←i-1
				A[i+1]←key

在这其中明显有嵌套循环，我们实际上关注循环，因为其他常数操作无关紧要，我们是对其渐进分析。第一个循环中是2到j，而内部循环是从无需的抽出元素对前面的有序序列做插入操作，实际上是由2到j次比对。也就是说，时间复杂度是θ($n^2$)。

那这个时间复杂度到底快不快呢？对于小的n它确实挺快，但是对于巨大的n它就不是那么回事了，所以在下面我会给你一个更快的算法。

1.2.2 归并排序

1.2.2.1 归并排序原理

让我们还是用抽象逐步讲到具体。我们给出一个对于A[1…n]的归并排序。

• 如果给定序列是1，自然不用排序，因为序列中只有一个元素。
• 否则进行递归，递归的每一层都会将序列一分为二，直到分出一个元素为止，然后对其一对一排序。
• 最后将排序后的序列全部重组。

这里我们出现一个新名词——递归，这个知识点实际上有点小难，我推荐你去看一下我写的博客数据结构杂谈番外篇——搞懂递归的小文章_弄鹊-CSDN博客。

上述归并算法关键的部分在于归并。归并实际上是使用了分治法的思想，先将大问题分解成小问题，然后再将小问题求解后合并结果。

假设我现在有这么一个数组 8 4 5 7 1 3 6 2，如果采用归并算法，我们是这么做的：

在我们使用递归进入最深层次（即不可再分的第三层）时，我们开始进行治，我们治的方式是用两根数组指针分别指向分开的两个序列，如下图所示：

这个操作的时间复杂度是θ(n)，因为我们所花时间都是在合并n次上。实际上分解并不耗费时间，因为每次递归分解都是分解一次。而每次合并要移动指针。

1.2.2.2 归并排序时间复杂度

让我们来看看整个归并排序的时间复杂度是多少。实际上归并排序总时间=子序列排好序时间+合并时间。

现在我们提前使用递归树方法来解决这里的问题，关于详细我们会在下一小节叙述：

假设我们有n个数的序列，那么第一次分就可以分为两个n/2的序列。

$T(n)=2\ast T(n/2)+合并时间$。又由于合并的时候按照我们上面所说是循环比较两个指针指向值的大小，所以复杂度为n。则我们可以改写$T(n)=2\ast T(n/2)+\theta (n)$。当然了，对于n = 1的情况，T(n) = 1，这个情况我们一般忽略，因为他对递归解没有影响。我们用显式的$c\ast n$来替换隐式的θ(n)，然后把其写出树状结构如下所示：

c* n指的是多个常数阶步骤所消耗的时间复杂度。常数阶的时间复杂度在进行渐进表示时通常省略，所以我们说他是隐式的，而我们用显式的c*n来表示这些步骤。因为我们在这个时候是要计算T(n)而不是$\Theta (n)$。

也就是说，这个递归树的每一层实际上都是cn。如第二层cn = T(n/2)+T(n/2)。那我们要计算递归树中所有结点所消耗的时间复杂度，即全部相加，用cn乘上树的高度即可。树的高度为lgn，所以在递归树中归并算法花费的时间复杂度为$cn\ast lgn$。这时候我们如果要求渐进时间复杂度，只需忽略常数项，所以由此可得归并排序时间复杂度为$\Theta (nlgn)$。

在计算机这一块领域中，lgn就是$lo{g}_{2}n$。我们设n除2分了一次，除2除了x次，那么最终$n/2^x$ = 1，通过指对互换进行反解，即$x=lo{g}_{2}n$。也就是说树的高度是$lo{g}_{2}n$。而lgn只不过是$lo{g}_{2}n$的常数倍，由渐进表示可知这个不影响。所以你要拿lgn表示$lo{g}_3、lo{g}_{4}n$也是可以的。