Python — 函数进阶(3)
文章目录
- 函数进阶(3)
-
- 递归
-
- 什么是递归
-
- 递归的优势
- 递归的风险
- 怎样实现递归
-
- 阶乘
- 斐波那契数列
-
- 缓存器对重复计算的优化
函数进阶(3)
本编是函数进阶的最后一篇文章,意在介绍函数中尤为重要的递归(recursion)。
这不仅仅是所有编程中的一种套路模板、算法,更是尤为重要的编程思想。
而这篇文章将通过详细讲解阶乘以及斐波那契数列(Fibonacci)来介绍递归。
递归
什么是递归
递归的定义
递归就是语句、表达式、函数自指的现象。
这里用到了一词语,“自指”;
说到“自指”就不得不提及吃自己尾巴的衔尾蛇了(如下图);

而对于编程而言,“自指”即是当一个语句、表达式、函数自己调用自己的时候便可以称为递归。
让我们来看一下最简单的递归是如何构成的,
def a():
print('我在调用我自己') # 打印输出任意字符便于观察运行状况
a() # 在函数代码体最后重新调用自己
a() # 正式调用
以上便形成了一个递归;
递归的优势
1)递归能够很大程度的减少书写地代码量;
2)能够完成复杂的算法操作;
3)递归是一种尤为重要地编程思想,对于任何一种语言都是通用的。
递归的风险
1)递归使用不恰当可能会对内存造成损伤(但是人性化的Python对于此早已就做出了限制);
2)盲目使用递归。
Python这款语言对于递归最多可以自指的次数做出了限制,在正常情况下最多只能够调用自己1000次。
而现在我就要介绍,怎么让这个限制解除,
import sys
sys.setrecursionlimit(1000000)
def a():
print('我在调用我自己')
a()
a()
'友情提示:做出危险操作前记得即时 ctrl+F2'
怎样实现递归
如果使用函数的话,递归的本质就是关于函数返回值的使用理解,
只有当对返回值这一概念理解到位才能够顺利编写出正确的递归使用方式。
阶乘
写一个阶乘函数:
1)对于正整数而言,输入参数是5的时候,给出的结果将会是54321
让我来试着通过函数来写一下,
def recursion(num,sum=1): # 定义一个recursion函数
if num>1: # 当传入的数大于1才会执行if中的代码体
sum *= num
return recursion(num-1,sum) # 重新调用recursion函数计算sum
return sum # 当传入的num不大于1的时候就代表着阶乘结束,返回结果
recursion(5)
# 第一次:判断出num>1,执行5*1,继续调用recursion(4,5)
# 第二次:判断出num>1,执行5*4,继续调用recursion(3,20)
# 第三次:判断出num>1,执行20*3,继续调用recursion(2,60)
# 第四次:判断出num>1,执行60*2,继续调用recursion(1,120)
# 第五次:……
如果说以上代码是一个刚刚接触递归这个概念读者写出来,那是相当不错的,
因为已经做到自己调用自己,并且出口明确(如果num不大于1则会返回结果);
但这个代码并不能够算是真正的递归,只能说是形似,
递归其实是分为两步,第一步是回推,第二步是递推;
def recursion(num):
if num == 1:
return 1
return num*recursion(num-1)
recursion(5) # 120
这才是最正确的递归,
让我们来拆解一下这个流程,并且介绍一下什么是回推和递推;
回推:
5*recursion(4)
5*4*recursion(3)
5*4*3*recursion(2)
5*4*3*2recursion(1)
5*4*3*21
递推:
5*4*3*2
5*4*6
5*24
120
回推是算式拆解的过程,而递推则是计算的过程,
在阶乘中这并不明显,稍后的斐波那契数列各位读者对于递归的认识又会有更深的理解。
斐波那契数列
写一个斐波那契数列:
1、1、2、3、5、8、13、21、34……
从以上数列中不难发现,除了第一个和第二个外,后一项都是前两项之和
好那么请使用递归将其编写出来
def fibonacci(num): # 定义一个fibonacci数列,传入的参数是数字索引位置(从1开始的)
if num ==1 or num ==2: # 当传入的数位于第1个或者第2个返回1
return 1
return fibonacci(num - 1) + fibonacci(num - 2)
fibonacci(8) # 21
fibonacci数列的回推、递推过程:
回推过程:
fibonacci(6)
fibonacci(5) + fibonacci(4)
fibonacci(4) + fibonacci(3) + fibonacci(4)
fibonacci(3) + fibonacci(2) + fibonacci(3) + fibonacci(4)
fibonacci(2) + fibonacci(1) + fibonacci(2) + fibonacci(3) + fibonacci(4)
fibonacci(2) + fibonacci(1) + fibonacci(2) + fibonacci(2) + fibonacci(1) + fibonacci(4)
fibonacci(2) + fibonacci(1) + fibonacci(2) + fibonacci(2) + fibonacci(1) + fibonacci(3) + fibonacci(2)
fibonacci(2) + fibonacci(1) + fibonacci(2) + fibonacci(2) + fibonacci(1) + fibonacci(2) + fibonacci(1) + fibonacci(2)
这就是点给我们调用了fibonacci(6)时候发生的回推过程,将斐波那契数量不断拆分成最细小的组成单元,
fibonacci(2)和fibonaaci(1)就是最小的单元,因为可以直接得到结果;
请好好注意一下过程,我们先把fibonacci(5)拆分最小的fibonacci(2) + fibonacci(1) + fibonacci(2) + fibonacci(2) + fibonacci(1)
然后再去拆解fibonacci(4),这很符合程序运行过程(后续讲解中会给出如何优化这个重复的步骤);
递推过程:
fibonacci(2) + fibonacci(1) + fibonacci(2) + fibonacci(2) + fibonacci(1) + fibonacci(2) + fibonacci(1) + fibonacci(2)
fibonacci(2) + fibonacci(1) + fibonacci(2) + fibonacci(2) + fibonacci(1) + fibonacci(2) + 2
fibonacci(2) + fibonacci(1) + fibonacci(2) + fibonacci(2) + fibonacci(1) + 3
fibonacci(2) + fibonacci(1) + fibonacci(2) + fibonacci(2) + 4
fibonacci(2) + fibonacci(1) + fibonacci(2) + 5
fibonacci(2) + fibonacci(1) + 6
fibonacci(2) + 7
8
在完成了最小单元的拆分之后便开始了计算,得到了最终结果8。
缓存器对重复计算的优化
在斐波那契数列回推的过程中,你会发现很多重复的步骤,
比如说:
fibonacci(6)
fibonacci(5) + fibonacci(4)
fibonacci(4) + fibonacci(3) + fibonacci(4)
你可以发现fibonacci(4)是重复计算了的,我们先拆解了第一个,然后又拆解了一遍第三个,
这种重复的事情对于计算机内存的占用是十分严重的,
但好在有一种方法可以优化这种内存占用的情况 —— 缓存器。
缓存器其实就是字典,可以通过字典来保存一下计算结果,并且用于下次计算,
请看看一下以下代码:
def fibonacci(num):
cache = {} # 定义一个空字典当作缓存器
if num == 1 or num == 2: # 找到1或者2位置的数就会返回1
return 1
if cache.get(num) is None: # 尝试着用cache.get(num)获取对应位置上的值(结果很想然是没有的)
cache[num] = fibonacci(num - 1) + fibonacci(num - 2) # 没有值我们就用递归赋值一个
else:
return cache[num]
程序运行拆解:
假设我们调用fibonacci(4)
1)判断5是否与1或者2相等,判断
cache.get(4)是否为None,执行赋值操作,发生递归调用cache[4] = fibonacci(3) + fibonacci(2);
2)判断3是否与1或者2相等,判断cache.get(3)是否为None,执行赋值操作,发生递归调用cache[3] = fibonacci(2) + fibonacci(1);
3)找到fibonacci(2),返回1;
4)找到fibonacci(1),返回1;
5)cache[3]得到结果;
6)计算fibonacci(2),返回1;
7)整合fibonacci(3) + fibonacci(2),给出结果。
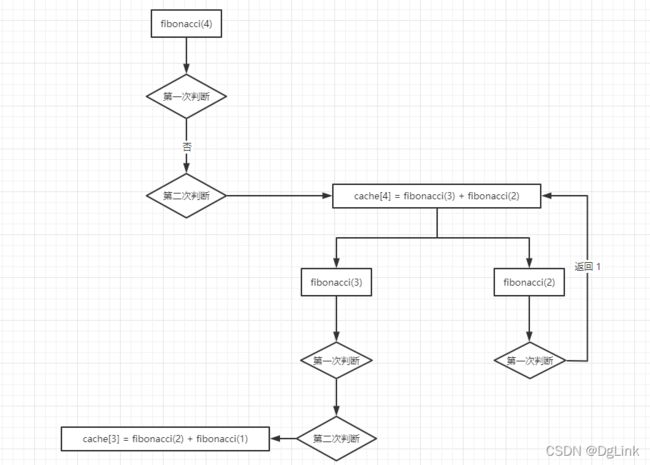
这就这个程序的工作原理;
然后我们满心欢喜的去运行这个程序,
却得到了一个报错,

类型错误,并不支持None类型的数据和int类型的数据进行相加减,
并且报错的地方就是 cache[num] = fibonacci(num - 1) + fibonacci(num - 2);
其实错误的地方很明显(没错,我故意的),
就是缺少一个返回值,
在流程图中其实我们就已经知道了,
在执行cache[3] = fibonacci(2) + fibonacci(1)我们没有将这个结果返回给cache[4] = fibonacci(3) + fibonacci(2)
所以我们稍微更改一下代码:
def fibonacci(num):
cache = {}
if num == 1 or num == 2:
return 1
if cache.get(num) is None:
cache[num] = fibonacci(num - 1) + fibonacci(num - 2)
return cache[num]
else:
return cache[num]
以上就是函数进阶(3)的全部内容,
觉得笔者写的不错的可以点赞支持,后续会更新Python面向对象的编程方法。
若是对本篇内容感兴趣的可以尝试着取用普通循环完成阶乘和斐波那契数列。
