算法刷题记录(Day 56)

复旦大学计算机学院2021夏令营机试

第一题

题目描述:给定一颗二叉树，树的每个节点的值为一个正整数。如果从根节点到节点 N 的路径上不存在比节点 N 的值大的节点，那么节点 N 被认为是树上的关键节点。求树上所有的关键节点的个数。请写出程序，并解释解题思路。

输入:

3, 1, 4, 3, null, 1, 5

解题思路:
dfs遍历一遍树上的所有节点，注意维护一个当前路径上最大值的变量max，当遍历到节点i，时，便和这个值进行比较，若大于该值，则节点数加上1，并更新变量max。否则，直接向下传递即可。时间复杂度为O(N)。

代码实现:

#include
using namespace std;
#define NMAX 10000
int tree[NMAX];
int N = 0;
char c;
int res = 0;
void dfs(int lot, int mmax) {
	if (tree[lot] >= mmax) {
		//printf("%d %d %d\n", lot, tree[lot], mmax);
		res++;
		mmax = tree[lot];
	}
	if (tree[2 * lot + 1]) dfs(2 * lot + 1, mmax);
	if (tree[2 * lot + 2]) dfs(2 * lot + 2, mmax);
}
int main() {
	FILE* stream;
	freopen_s(&stream, "C:\\Users\\芙茗\\\Desktop\\保研相关\\test.in", "r", stdin);
	while (scanf_s("%c", &c)==1 ) {
		if (c >= '1' && c <= '9') tree[N++] = c - '0';
		else if (c == 'n') tree[N++] = 0;
	}
	dfs(0, 0);
	printf("%d\n", res);
}

测试过程:

In:3, 1, 4, 3, null, 1, 5
Out:4

In:3， 4，7， 5，2，8，9，null, null, 3, 9
Out:7

第二题

题目描述:训练场上有一个台阶，总共有 n 级。一个运动员可以跳 1 级，也可以跳 2 级。求运动员有多少种跳法。请写出程序，并解释解题思路。

解题思路:动态规划，假设dp[i]代表的是跳i级台阶的跳法，那么dp[i]=dp[i-1]+dp[i-2]，因此时间复杂度为O(n)。
如果n很大的话，可能会超时，所以转化为如下所示的矩阵方式进行处理。a的初始值为dp[1]=1,b的初始值为dp[2]=1，假设需要跳的步数为n，则需要方阵需要n-2次幂，最后再乘上[1,1]。时间复杂度为O(logn)，空间复杂度为O(1)。

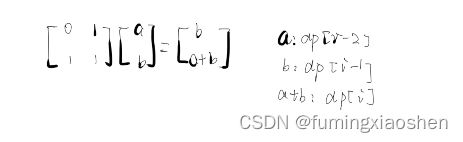
代码实现:

#include
using namespace std;
#define dimension 2
int n;
long long G[dimension][dimension] = { {0,1},{1,1} };
long long O[dimension][dimension] = { {1,0},{0,1} };
long long res[dimension][dimension] = { {0,0},{1,0} };
void mul(long long a[][dimension], long long b[][dimension], long long c[][dimension]) {
	long long tmp[dimension][dimension];
	for (int i = 0; i < dimension; i++) {
		for (int j = 0; j < dimension; j++) {
			tmp[i][j] = 0;
			for (int k = 0; k < dimension; k++) {
				tmp[i][j] += b[i][k] * c[k][j];
			}
		}
	}

	memcpy(a, tmp, sizeof(tmp));
}
int main() {
	scanf_s("%d", &n);
	while (n) {
		if (n % 2) {
			mul(O, O, G);
		}
		mul(G, G, G);
		n /= 2;
	}
	mul(res, O, res);
	printf("%lld\n", res[1][0]);
}

tip: 矩阵乘法的最后一定是memcpy(a, tmp, sizeof(tmp));，不能是memcpy(a, tmp,sizeof(a));
可以观察到,a仅仅只是被解析为了一个指针。

第三题

题目描述:

解题思路:暴力枚举的范围会达到O(2ⁿ)。转化为动态规划，dp[E][n][2]用于动态规划过程中的数组，dp[e][i][0]代表的是第i个取正数时，和为e的取法个数，dp[e][i][1]则代表的时取负数时的取法个数
i从小到大进行遍历，e从小到大，双层循环，时间复杂度为O(e*n)。(注意遍历的顺序)
递推关系为dp[e][i][0]=dp[e-cost[i]][i-1][0],dp[e-cost[i]][i-1][1] dp[e][i][1]=dp[e+cost[i]][i-1][1]+dp[e+cost[i]][i][0]

#include
using namespace std;
#define NMAX 1000
#define EMAX 1000
int n = 0, E;
int num[NMAX];
long long sum;
long long dp[EMAX][NMAX][2];
int main() {
	FILE* stream;
	freopen_s(&stream, "C:\\Users\\芙茗\\\Desktop\\保研相关\\test.in", "r", stdin);
	while (scanf_s("%d", &num[n++]) == 1) sum += num[n - 1];
	E = num[n - 2];//注意没有读取成功后n会加一
	n-=2;
	memset(dp, 0, sizeof(dp));
	dp[sum+num[0]][0][0] = 1;
	dp[sum -num[0]][0][0] = 1;
	for (int i = 1; i < n; i++) {
		for (int e = 0; e <= 2*sum; e++) {
			if(e-num[i]>=0 )dp[e][i][0] = dp[e - num[i]][i - 1][0] + dp[e - num[i]][i - 1][1]; 
			dp[e][i][1] = dp[e + num[i]][i - 1][1] + dp[e + num[i]][i - 1][0];
		}
	}
	printf("%lld", dp[E+sum][n - 1][0] + dp[E+sum][n - 1][1]);
}

tip: 注意该题可能会有负数，因此首先需要计算出所有元素的和以确定边界，然后再加上一个基准sum,即可实现