数据结构之二叉树先序后续中序遍历

二叉树的遍历：

二叉树的遍历（traversing binary tree）是指从根结点出发，按照某种次序依次访问二叉树中所有结点，使得每个结点被访问一次且仅被访问一次。（二叉树的遍历方式可以很多，如果限制从左到右的方式，那么主要分为四种）

先序遍历（根左右）：（也称为前序遍历）

若二叉树为空，则空操作返回，否则先访问根结点，然后前序遍历左子树，再前序遍历右子树，即以“根左右”的顺序进行遍历。
下图中的二叉树前序遍历（假设遍历即为输出该结点数据）：
1、整棵树的根结点为A，由于前序遍历顺序为“根->左子树->右子树”，故先输出A
2、遍历左子树，其根结点为B，故输出B，此时已经得到了：AB
3、遍历左子树的左子树，其根结点为D，故输出D，此时得到：ABD
4、由于结点D没有左子树和右子树，故根结点B的左子树已经遍历完，接下来遍历其右子树
5、根结点B的右子树的根结点为E，输出E，此时得到：ABDE
6、遍历根结点E的左子树，其根结点为G，输出G，得到：ABDEG
7、遍历根结点E的右子树，其根结点为H，输出H，得到：ABDEGH
8、此时整棵子树的左子树已经遍历完成，开始遍历右子树
9、根结点A的右子树的根结点为C，故输出C，得到：ABDEGHC
10、再遍历其左子树，其根结点为F，输出F，得到：ABDEGHCF，遍历完成。
注：时刻以“根->左->右”的顺序遍历，由于根在最前，故称为前序遍历

中序遍历（左根右）：

若二叉树为空，则空操作返回，否则从根结点开始（注意并不是先访问根结点）， 中序遍历根结点的左子树，然后是访问根结点，最后中序遍历右子树。上图中的二叉树中序遍历结果为：DBGEHAFC

后序遍历（左右根）：

若二叉树为空，则空操作返回，否则从左到右先叶子后结点的方式遍历访问左右子树，最后访问根结点。上图中的二叉树后序遍历结果为：DGHEBFCA

层序遍历：

若树为空，则空操作返回，否则从树的第一层，也就是根结点开始访问，从上而下逐层遍历，在同一层中，按从左到右的顺序对结点逐个访问。上图中的二叉树层序遍历结果为：ABCDEFGH

已知先序和中序求后序，例如若二叉树的先序遍历序列为ABDECF，中序遍历序列为DBEAFC，则其后序遍历序列为（）。 A．DEBAFC         B．DEFBCA         C．DEBCFA         D．DEBFCA

答案选D

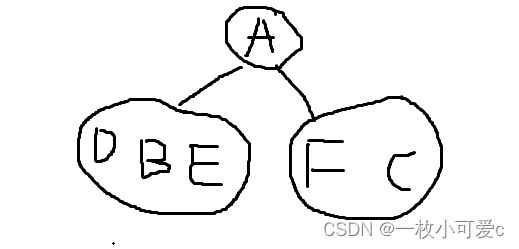
分析：先构建出二叉树，先看先序，由于先序是根左右而且A在第一个位置，所以A是根节点，再看中序，由于中序是左根右，所以在中序里面，A左边（DBE）的位于根节点的左面，A右面（FC）的位于跟节点的右面也就是现在可以确定的二叉树的大致结构为

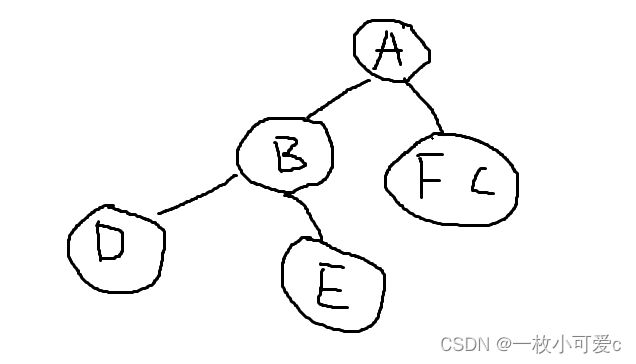
再对DBE进行分析，在先序里B处于BDE的第一个位置，所以B是中间节点，再看中序D位于B的左面，所以B是D的左孩子，同理E是B的右孩子，因此可以得出进一步的二叉树的结构

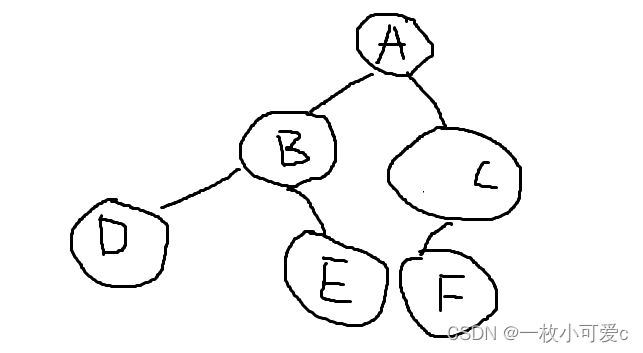
依次迭代后可以确定二叉树的结构为

最后通过上面的讲解可以看出后序为DEBFCA

关于二叉树定义，先序遍历，中序遍历，后序遍历，翻转二叉树，求二叉树最大最小深度，有序数组转成二叉树的Java代码

import java.util.List;

public class Solution {

    //定义二叉树
    static class TreeNode {
        int val;//根节点
        TreeNode left;//左节点
        TreeNode right;//右节点
        public TreeNode(int key) {
            left = null;
            right = null;
            this.val = key;
        }
    }

    //先序遍历
    public void preorder(TreeNode root, List res) {
        if (root == null) {
            return;
        }
        res.add(root.val);
        preorder(root.left, res);
        preorder(root.right, res);
    }

    //中序遍历
    public void inorder(TreeNode root, List res) {
        if (root == null) {
            return;
        }
        inorder(root.left, res);
        res.add(root.val);
        inorder(root.right, res);
    }
    
    //后序遍历
    public void postorder(TreeNode root, List res) {
        if (root == null) {
            return;
        }
        postorder(root.left, res);
        postorder(root.right, res);
        res.add(root.val);
    }
    
    //翻转二叉树
    public TreeNode invertTree(TreeNode root) {
        if (root == null) {
            return null;
        }
        TreeNode left = invertTree(root.left);
        TreeNode right = invertTree(root.right);
        root.left = right;
        root.right = left;
        return root;
    }
    
    //二叉树的最大深度
    public int maxDepth(TreeNode root) {
        if (root == null) {
            return 0;
        } else {
            int leftHeight = maxDepth(root.left);
            int rightHeight = maxDepth(root.right);
            return Math.max(leftHeight, rightHeight) + 1;
        }
    }
    
    //二叉树的最小深度
    public int minDepth(TreeNode root) {
        if (root == null) {
            return 0;
        }

        if (root.left == null && root.right == null) {
            return 1;
        }

        int min_depth = Integer.MAX_VALUE;
        if (root.left != null) {
            min_depth = Math.min(minDepth(root.left), min_depth);
        }
        if (root.right != null) {
            min_depth = Math.min(minDepth(root.right), min_depth);
        }

        return min_depth + 1;
    }

    //将有序数组转成二叉树   //第一次迭代时left=0，right=nums.length-1
    public TreeNode helper(int[] nums, int left, int right) {
        if (left > right) {
            return null;
        }
        // 总是选择中间位置左边的数字作为根节点
        int mid = (left + right) / 2;
        TreeNode root = new TreeNode(nums[mid]);
        root.left = helper(nums, left, mid - 1);
        root.right = helper(nums, mid + 1, right);
        return root;
    }

}