软件设计师考试笔记--------数据结构基础2:KMP算法
软件设计师考试笔记--------数据结构基础2:KMP算法
重点:必须学会部分匹配表的计算方式以及最后考试例题的解法,几乎必考!
1.1 KMP算法
*KMP算法是一种改进的字符串匹配算法。
*KMP算法的关键是利用匹配失败后的信息,尽量减少模式串与主串的匹配次数以达到快速匹配的目的。具体实现就是实现一个next()函数,函数本身包含了模式串的局部匹配信息。
*KMP算法的想法是,利用已经知道的前面六个字符“ABCDAB”,不要把“搜索位置”移回已经比较过的位置,继续把它向后移,这样就提高了效率。
*学会计算《部分匹配表》:
首先了解两个概念:“前缀”和“后缀”。
*”前缀”指除了最后一个字符以外,一个字符串的全部头 部组合;
*”后缀”指除了第一个字符以外,一个字符串的全部尾部组合。
*匹配时移动的步数是用当前已匹配字符串的长度减去已匹配字符串中的最后一位在部分匹配表中对应的值所得出的。
“部分匹配值”就是“前缀”和“后缀”的最长的共有元素的长度。以“ABCDABD”为例:
-“A”的前缀和后缀都为空集,共有元素的长度为0;
-“AB”的前缀为[A],后缀为[B],共有元素的长度为0;
-“ABC”的前缀为[A,AB],后缀为[BC,C],共有元素的长度为0;
-“ABCD”的前缀为[A,AB,ABC,],后缀为[BCD,CD,D],共有元素长度为0;
-“ABCDA”的前缀为[A,AB,ABC,ABCD],后缀为[BCDA,CDA,DA,A],最长共有元素为”A”,长度为1;
-“ABCDAB”的前缀为[A,AB,ABC,ABCD,ABCDA],后缀为[BCDAB,CDAB,DAB,AB,B],最长共有元素为“AB”,长度为2;
-“ABCDABD”的前缀为[A,AB,ABC,ABCD,ABCDA,ABCDAB],后缀为[BCDABD,CDABD,DABD,ABD,BD,D],共有元素的长度为0。
得出:

考试例题:
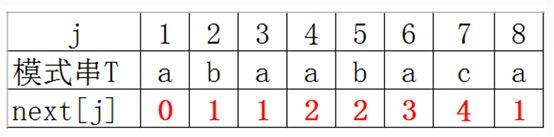
在字符串的KMP模式匹配算法中,需先求解模式串p的 next函数值,其定义如下。若模式串p为“abaabaca”,则其 next函数值为(B)

A.01111111 B.01122341 C.01234567 D.01122334
解: 给定的字符串叫做模式串T。j表示next函数的参数,其值是从 1到n,n是模式串T的长度。而k则表示一种情况下的next函数值。p表示其中的某 个字符,下标从1开始。看等式左右对应的字符是否相等。


式子思路:前面的式子计算时p1开头,pk-1结尾,后面的式子同理。k以前所有符合条件的k,就是式子的长度,k值从符合条件的最大值开始依次递减进行计算。
按照上述思路和公式具体计算如下:
1、j=1时,next[1]=0;
2、j=2时,k的取值为(1,j)的开区间,所以整数k是不存在的, 那就是第三种情况,next[2]=1;
3、j=3时,k的取值为(1,3)的开区间,k从最大的开始取值, 然后带入含p的式子中验证等式是否
成立,不成立k取第二大 的值。现在是k=2,将k导入p的式子中得,p1=p2,即 “a”=“b”,显然不成立,舍去。k再取值就超出范围了,所以 next[3]不属于第二种情况,那就是第三种了,即next[3]=1;
4、j=4时,k的取值为(1,4)的开区间,先取k=3,将k导入p 的式子中得,p1p2=p2p3,不成立。 再取k=2,得p1=p3,成 立。所以next[4]=2;
5、j=5时,k的取值为(1,5)的开区间,先取k=4,将k导入p 的式子中得,p1p2p3=p2p3p4,不成立。 再取k=3,得 p1p2=p3p4,不成立。 再取k=2,得p1=p4,成立。所以 next[5]=2;
6、j=6时,k的取值为(1,6)的开区间,先取k=5,将k导入p 的式子中得,p1p2p3p4=p2p3p4p5,不成立。 取k=4,得 p1p2p3=p3p4p5,不成立。再取k=3,将k导入p的式子中得, p1p2=p4p5,成立。所以next[6]=3;
7、j=7时,k的取值为(1,7)的开区间,先取k=6,将k导入p 的式子中得,p1p2p3p4p5=p2p3p4p5p6,不成立。 再取k=5, 得 p1p2p3p4=p3p4p5p6 ,不成立。 再取k=4,得 p1p2p3=p4p5p6 ,成立。所以next[7]=4;
8、j=8时,k的取值为(1,8)的开区间, 先取k=7,将k导入 p的式子中得,p1p2p3p4p5p6=p2p3p4p5p6p7,不成立。 再 取k=6,得p1p2p3p4p5=p3p4p5p6p7,不成立。… 再取k=2, 得p1=p7,不成立。k再取值就超出范围了,所以next[8]不属 于第二种情况,那就是第三种了,即next[8]=1;结果如下: