算法：根据二叉树的中序遍历以及前/后序遍历，求出后/前序遍历（中间包含二叉树的生成算法）

经常我们会看到这样的问题，那就是给出二叉树的前序遍历和中序遍历，求后序遍历。或者给出二叉树的后序遍历和中序遍历，求前序遍历。正所谓是难者不会，会者不难，今天我就实现这个算法，并分享给大家

二叉树的三种遍历，知道其中两个，便可得到剩下的一个。中序遍历是必须知道的，然后前后序再知道一个，其实就可以得到这个二叉树了。得到了二叉树，也就得到了三种遍历顺序了

所以，我的算法思路也就如下：
1、先根据两种已知的遍历顺序，构建出二叉树
2、再将二叉树以所求的顺序进行遍历，便可得到结果

下面是我们验证程序的示例二叉树：

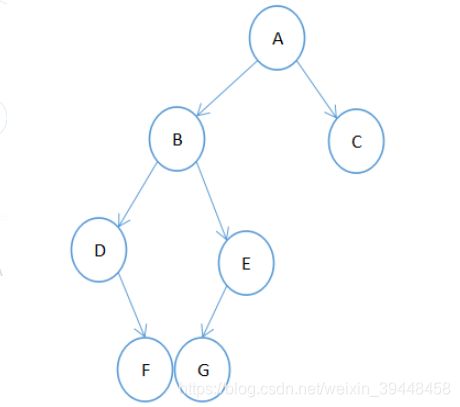
遍历二叉树的方法分别有前序遍历、中序遍历、后序遍历：
前序遍历：先遍历根节点，然后是左子树，最后是右子树；根节点 -> 左子树 -> 右子树
中序遍历：先遍历左子树，然后是根节点、最后是右子树；左子树 -> 根节点 -> 右子树
后序遍历：先遍历左子树，然后是右子树，最后是根节点；左子树 -> 右子树 -> 根节点

所以，我们可以得到，上面示例二叉树的三种遍历顺序为：
前序遍历：ABDFEGC
中序遍历：DFBGEAC
后序遍历：FDGEBCA

接下来是我实现 “先序 + 中序 -> 后序” 和 “后序 + 中序 -> 先序” 的Java代码，算法的精髓都在代码和其间的详细注释中，读者可以复制到IDE里面去运行，然后DEBUG模式研究算法的详细步骤，也可以直接阅读算法实现代码：

Node.java：二叉树的结点类，数据我们用String：

import java.util.List;

/**
 * 二叉树的节点类
 * @Author: LiYang
 * @Date: 2019/10/27 1:15
 */
public class Node {

    //二叉树的内容（本例用String内容）
    public String data;

    //左节点
    public Node lChild;

    //右节点
    public Node rChild;

    /**
     * 如果打印的话，就打印节点的数据字符串
     * @return
     */
    @Override
    public String toString() {
        return this.data;
    }

    /**
     * 二叉树的前序遍历
     * @param root 二叉树根节点
     * @param orderList 前序遍历的结果集合
     */
    public static void preOrderTraversal(Node root, List<Node> orderList){
        if(root != null){
            //先遍历根（装结果集合）
            orderList.add(root);

            //再遍历左子树
            preOrderTraversal(root.lChild, orderList);

            //最后遍历右子树
            preOrderTraversal(root.rChild, orderList);
        }
    }

    /**
     * 二叉树的中序遍历
     * @param root 二叉树根节点
     * @param orderList 中序遍历的结果集合
     */
    public static void midOrderTraversal(Node root, List<Node> orderList){
        if(root != null){
            //先遍历左子树
            midOrderTraversal(root.lChild, orderList);

            //再遍历根（装结果集合）
            orderList.add(root);

            //最后遍历右子树
            midOrderTraversal(root.rChild, orderList);
        }
    }

    /**
     * 二叉树的后序遍历
     * @param root 二叉树根节点
     * @param orderList 后序遍历的结果集合
     */
    public static void postOrderTraversal(Node root, List<Node> orderList){
        if(root != null){
            //先遍历左子树
            postOrderTraversal(root.lChild, orderList);

            //再遍历右子树
            postOrderTraversal(root.rChild, orderList);

            //最后遍历根（装结果集合）
            orderList.add(root);
        }
    }

}

BinaryTreeOrder.java：二叉树遍历顺序解答类，实现两种求顺序的算法：

import java.util.ArrayList;
import java.util.List;

/**
 * 二叉树遍历顺序解答类：
 * 已知中序遍历和前/后序遍历，求后/前序遍历
 * @Author: LiYang
 * @Date: 2019/10/27 1:17
 */
public class BinaryTreeOrder {

    /**
     * 根据三种遍历顺序，生成对应的二叉树
     * 注意，必须存在中序遍历，前后序需要其中之一
     * @param pre 前序遍历结果
     * @param mid 中序遍历结果
     * @param post 后续遍历结果
     * @return 生成二叉树的根节点
     */
    public static Node generateBinaryTree(List<String> pre, List<String> mid, List<String> post){
        //根节点
        Node root = new Node();

        //如果后序List为空，则是根据前中序求后序
        if (post == null){
            parsePostOrder(root, pre, mid);
        }

        //如果前序List为空，则是根据中后序求前序
        if (pre == null){
            parsePreOrder(root, mid, post);
        }

        //返回最后生成的二叉树的根节点
        return root;
    }

    /**
     * 已知前序中序的遍历结果，生成以传入节点为根的二叉树
     * @param root 生成的二叉树的根
     * @param pre 前序遍历结果
     * @param mid 中序遍历结果
     */
    public static void parsePostOrder(Node root, List<String> pre, List<String> mid){
        //获得根节点的数据
        String rootData = pre.get(0);

        //赋值根节点的数据
        root.data = rootData;

        //求中序遍历的根节点左右的两个子集合
        boolean meetMid = false;
        //中序遍历的左集合
        List<String> midLeftSub = new ArrayList<String>();
        //中序遍历的右集合
        List<String> midRightSub = new ArrayList<String>();

        //遍历求中序遍历的两个子集合
        for (String item : mid){
            if (item.equals(rootData)){
                meetMid = true;
                continue;
            }

            if (!meetMid){
                midLeftSub.add(item);
            } else {
                midRightSub.add(item);
            }
        }

        //求前序遍历的左子集合
        List<String> preLeftSub = pre.subList(1, midLeftSub.size() + 1);
        //求前序遍历的右子集合
        List<String> preRightSub = pre.subList(midLeftSub.size() + 1, pre.size());

        //如果前序和中序的左子集合都有内容
        if (preLeftSub.size() > 0 && midLeftSub.size() > 0){
            //实例化左子树的根
            root.lChild = new Node();

            //递归调用，解析左子集合
            parsePostOrder(root.lChild, preLeftSub, midLeftSub);
        }

        //如果前序和中序的右子集合都有内容
        if (preRightSub.size() > 0 && midRightSub.size() > 0){
            //实例化右子树的根
            root.rChild = new Node();

            //递归调用，解析右子集合
            parsePostOrder(root.rChild, preRightSub, midRightSub);
        }
    }

    /**
     * 已知中序后序的遍历结果，生成以传入节点为根的二叉树
     * @param root 生成的二叉树的根
     * @param mid 中序遍历的结果
     * @param post 后序遍历的结果
     */
    public static void parsePreOrder(Node root, List<String> mid, List<String> post){
        //获得根节点的数据
        String rootData = post.get(post.size() - 1);

        //赋值根节点的数据
        root.data = rootData;

        //求中序遍历的根节点左右的两个子集合
        boolean meetMid = false;
        //中序遍历的左集合
        List<String> midLeftSub = new ArrayList<String>();
        //中序遍历的右集合
        List<String> midRightSub = new ArrayList<String>();

        //遍历求中序遍历的两个子集合
        for (String item : mid){
            if (item.equals(rootData)){
                meetMid = true;
                continue;
            }

            if (!meetMid){
                midLeftSub.add(item);
            } else {
                midRightSub.add(item);
            }
        }

        //求后序遍历的左子集合
        List<String> postLeftSub = post.subList(0, midLeftSub.size());
        //求后序遍历的右子集合
        List<String> postRightSub = post.subList(midLeftSub.size(), post.size() - 1);

        //如果中序和后序的左子集合都有内容
        if (postLeftSub.size() > 0 && midLeftSub.size() > 0){
            //实例化左子树的根
            root.lChild = new Node();

            //递归调用，解析左子集合
            parsePreOrder(root.lChild, midLeftSub, postLeftSub);
        }

        //如果中序和后序的右子集合都有内容
        if (postRightSub.size() > 0 && midRightSub.size() > 0){
            //实例化右子树的根
            root.rChild = new Node();

            //递归调用，解析右子集合
            parsePreOrder(root.rChild, midRightSub, postRightSub);
        }
    }

    /**
     * 最终调用的方法（重要）：根据前序和中序，求后序
     * @param pre 前序遍历
     * @param mid 中序遍历
     * @return 后序遍历
     */
    public static List<Node> calculatePostOrder(List<String> pre, List<String> mid){
        //先根据前序和中序遍历，生成二叉树，返回根节点
        Node nodePost = generateBinaryTree(pre, mid, null);

        //后序遍历的集合
        List<Node> postOrderList = new ArrayList<Node>();

        //对二叉树进行后序遍历，结果装在上面的集合中
        Node.postOrderTraversal(nodePost, postOrderList);

        //返回后序遍历的结果集合（也可以转化List为List）
        return postOrderList;
    }

    /**
     * 最终调用的方法（重要）：根据中序和后序，求前序
     * @param mid 中序遍历
     * @param post 后序遍历
     * @return 前序遍历
     */
    public static List<Node> calculatePreOrder(List<String> mid, List<String> post){
        //先根据中序和后序遍历，生成二叉树，返回根节点
        Node nodePre = generateBinaryTree(null, mid, post);

        //前序遍历的集合
        List<Node> preOrderList = new ArrayList<Node>();

        //对二叉树进行前序遍历，结果装在上的集合中
        Node.preOrderTraversal(nodePre, preOrderList);

        //返回前序遍历的结果集合（也可以转化List为List）
        return preOrderList;
    }

    /**
     * 测试二叉树遍历的求解程序
     * @param args
     */
    public static void main(String[] args) {
        //示例二叉树的前序遍历：ABDFEGC
        List<String> pre = new ArrayList<String>();
        pre.add("A");
        pre.add("B");
        pre.add("D");
        pre.add("F");
        pre.add("E");
        pre.add("G");
        pre.add("C");

        //示例二叉树的中序遍历：DFBGEAC
        List<String> mid = new ArrayList<String>();
        mid.add("D");
        mid.add("F");
        mid.add("B");
        mid.add("G");
        mid.add("E");
        mid.add("A");
        mid.add("C");

        //示例二叉树的后续遍历：FDGEBCA
        List<String> post = new ArrayList<String>();
        post.add("F");
        post.add("D");
        post.add("G");
        post.add("E");
        post.add("B");
        post.add("C");
        post.add("A");

        /**
         * 测试根据前序和中序遍历，求后序遍历
         */
        List<Node> postOrderList = calculatePostOrder(pre, mid);

        //打印后序遍历的结果，并进行验证
        System.out.println("已知前序中序，求后序：" + postOrderList);

        /**
         * 测试根据中序和后序遍历，求前序遍历
         */
        List<Node> preOrderList = calculatePreOrder(mid, post);

        //打印前序遍历的结果，并进行验证
        System.out.print("已知中序后序，求前序：" + preOrderList);
    }

}

运行BinaryTreeOrder类的main方法测试算法，控制台输出：

已知前序中序，求后序：[F, D, G, E, B, C, A]
已知中序后序，求前序：[A, B, D, F, E, G, C]

输出的结果与预想的顺序一模一样，测试通过！这下读者们就不用怕这类问题了。如果不知道这类问题的答案，就把main方法的pre(前序遍历集合)、mid(中序遍历集合)、post(后序遍历集合)改为已知条件的顺序，然后运行程序，就可以得到答案了