统计学_蒙特卡罗方法

1、蒙特卡罗方法的基本思想

蒙特卡罗方法(Monte Carlo method)是由冯诺依曼和乌拉姆等人发明的，“蒙特卡罗”这个名字是出自摩纳哥的蒙特卡罗赌场，这个方法是一类基于概率的方法的统称，不是特指一种方法。

蒙特卡罗方法也成统计模拟方法，是指使用随机数（或者更常见的伪随机数）来解决很多计算问题的方法。他的工作原理就是两件事：不断抽样、逐渐逼近。下面用两个例子[1]来理解一下这个方法的思想。

（1）圆周率π值求解

如图所示，有一个半径为r=1的圆和边长为1的正方形，圆的面积为，则正方形内部的相切圆的面积为整个圆的1/4，也就是 π/4 ，正方形的面积为1。然后我们向正方形中随机打点，就会有一定的概率落在圆中：

这样我们就可以得到落在圆中的概率就是=圆的面积/正方形面积= π/4，那么就可以推出圆周率的计算公式：

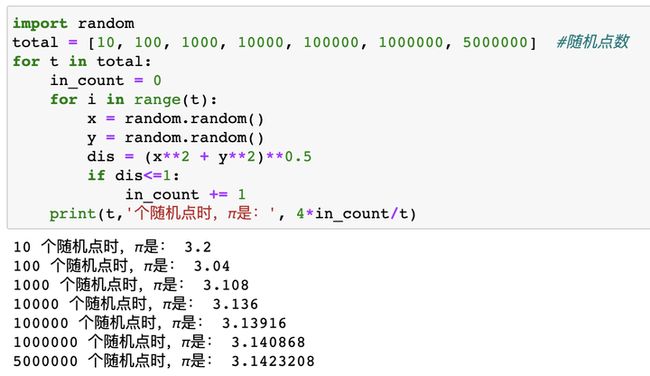
其中红色点可以定义为距离圆点距离小于1的点，可以通过python实现来看一下：

import random
total = [10, 100, 1000, 10000, 100000, 1000000, 5000000]  #随机点数
for t in total:
    in_count = 0
    for i in range(t):
        x = random.random()
        y = random.random()
        dis = (x**2 + y**2)**0.5
        if dis<=1:
            in_count += 1
    print(t,'个随机点时，π是：', 4*in_count/t)

可以看出随着随机点数的增加，近似度逐渐增大。

（2）计算不规则图形面积

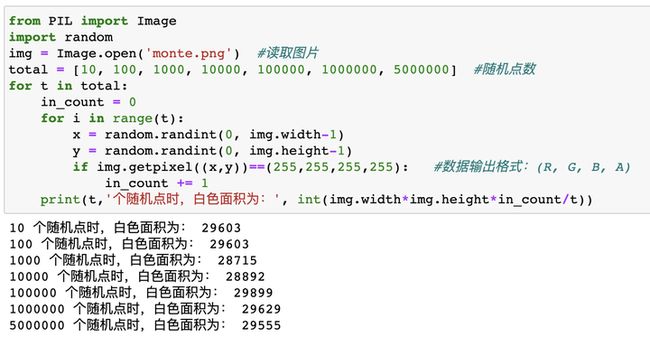
比如下面这张黑底图片，想要计算图中白色图形的面积，其中图形都是不规则图形，我们没办法通过边长公式等进行计算，其中一种方法就是可以通过蒙特卡罗方法，向图上随机打点，然后获取像素点所在的颜色，白色面积=白色点数/总点数*图片总面积（当然其实可以用计算机遍历所有像素点也可以求，但这里主要用来说明蒙特卡罗思想的方法）

下面还是通过python进行实现：

from PIL import Image
import random
img = Image.open('monte.png')  #读取图片
total = [10, 100, 1000, 10000, 100000, 1000000, 5000000]  #随机点数
for t in total:
    in_count = 0
    for i in range(t):
        x = random.randint(0, img.width-1)
        y = random.randint(0, img.height-1)
        if img.getpixel((x,y))==(255,255,255,255):   #数据输出格式：(R, G, B, A)
            in_count += 1
    print(t,'个随机点时，白色面积为：', int(img.width*img.height*in_count/t))

通过上面两个例子我们可以理解蒙特卡罗算法的一个基本思想，其实就是通过随机点来模拟实际的情况，不断抽样以逼近真实值。

由蒙特卡洛法得出的值并不是一个精确值，而是一个近似值，而且当投点的数量越来越大时，这个近似值也越接近真实值。

2、蒙特卡罗方法的应用

通常蒙特卡罗方法可以粗略地分成两类[2]：

一类是所求解的问题本身具有内在的随机性，借助计算机的运算能力可以直接模拟这种随机的过程。例如在核物理研究中，分析中子在反应堆中的传输过程。中子与原子核作用受到量子力学规律的制约，人们只能知道它们相互作用发生的概率，却无法准确获得中子与原子核作用时的位置以及裂变产生的新中子的行进速率和方向。科学家依据其概率进行随机抽样得到裂变位置、速度和方向，这样模拟大量中子的行为后，经过统计就能获得中子传输的范围，作为反应堆设计的依据。

另一种类型是所求解问题可以转化为某种随机分布的特征数，比如随机事件出现的概率，或者随机变量的期望值。通过随机抽样的方法，以随机事件出现的频率估计其概率，或者以抽样的数字特征估算随机变量的数字特征，并将其作为问题的解。这种方法多用于求解复杂的多维积分问题。

3、蒙特卡罗方法求定积分

比如积分，如果f(x)的原函数很难求解，那么这个积分也会很难求解。

那么我们如何通过蒙特卡罗方法对其进行模拟求解呢？

这时可以用一个比较容易算得面积的矩型罩在函数的积分区间上（假设其面积为Area），然后随机地向这个矩形框里面投点，其中落在函数f(x)下方的点为绿色，其它点为红色，然后统计绿色点的数量占所有点（红色+绿色）数量的比例为r，那么就可以据此估算出函数f(x)从 a 到 b 的定积分为 Area × r。

（2）平均值法（期望法）

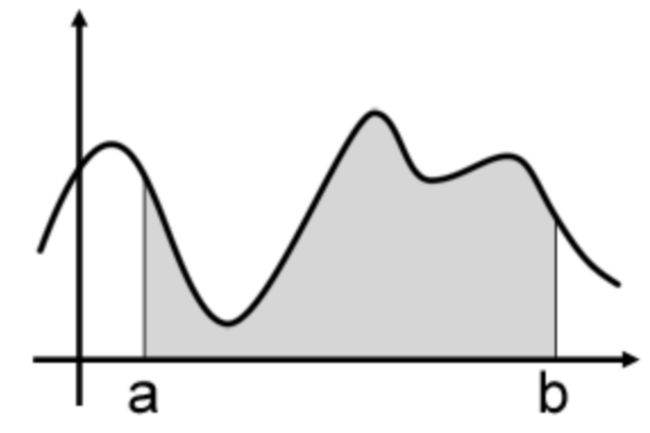
如下图所示，在[a,b]之间随机取一点x时，它对应的函数值就是f(x)，我们要计算，就是图中阴影部分的面积。

一个简单的近似求解方法就是用 来粗略估计曲线下方的面积，在[a,b]之间随机取点x，用f(x)代表在[a,b]上所有f(x)的值，如下图所示：

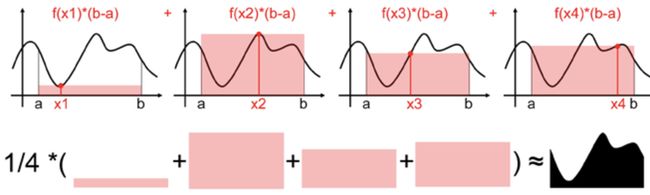
用一个值代表[a,b]区间上所有的 ( )的值太粗糙了，我们可以进一步抽样更多的点，比如下图抽样了四个随机样本 （满足均匀分布），每个样本都能求出一个近似面积值 ，然后计算他们的数学期望，就是蒙特卡罗计算积分的平均值法了。

 

参考：蒙特卡罗方法详解 - 知乎