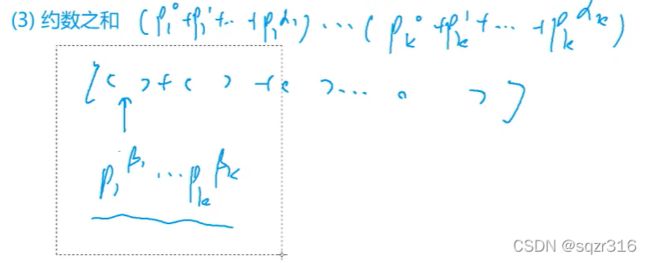【Acwing算法基础】数学知识01笔记
1.质数
- 质数:在大于1的整数中,如果只包含1和本身两个约数,就被称为质数,或者叫素数。
1.1 质数的判定——试除法
时间复杂度:O(sqrt(n))
package acwing;
import java.io.IOException;
import java.util.Scanner;
public class 判断质数_试除法 {
public static void main(String[] args) throws IOException {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
System.out.println(is_prime(n));
}
static boolean is_prime(int n) {
if (n < 2) return false;
// 这里 i < n可以优化
// 如果n % d == 0, 那么一定有 n / d = x,可以整除,所以n / d也可以整除n
// 那么只需要枚举小的数就可以了,大的可以不枚举,就可以判断了
// 所以 d <= n/d 取等号是因为 d可能会等于 n / d 即是同一个数
// 写成 i < n / i, 不推荐写成 i < sqrt(n)比较慢,i * i < n, 可能会溢出
for (int i = 2; i < n / i; i++) {
if (n % i == 0) return false;
}
return true;
}
}
1.2 分解质因数——试除法
时间复杂度:O(sqrt(n)) 当n = 2^k时,最小可以达到log(n) 。
思路:从小到达尝试所有数。
package acwing;
import java.util.Scanner;
public class 分解质因数_试除法 {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
while (n > 0) {
n--;
int x = sc.nextInt();
divid(x);
}
}
static void divid(int n) {
/**
n中最多只包含一个大于sqrt(n)的质因子,如果有2个大于sqrt(n)的质因子
乘在一起,那就大于n了。
基于此,i枚举到 n / i就可以了也就是,枚举到sqrt(n)
*/
for (int i = 2; i <= n / i; i++) {
// 分解质因数
/**
从小到大枚举,此时n中不包含2 ~ i-1之间的质因子
那么如果i是一个合数,并且n % i == 0, 那么n一定会包含i的质因子(2~i-1) 与上面矛盾
所以i一定是质数。
也可以理解为:大的合数,并且可以整除n的数字,一定会被小的可以整除n的质数筛掉
*/
if (n % i == 0) {
// 求一下i的次数
int s = 0;
while (n % i == 0) {
n /= i;
s++;
}
System.out.printf("%d %d\n", i, s);
}
}
// 由于枚举到sqrt(n),那么这时候n > 1,剩下的那个就是比较大的质因子
if (n > 1) System.out.printf("%d %d\n", n, 1);
}
}
1.3 筛质数
1.3.1 埃氏筛法
使用小的质数筛掉大的合数
时间复杂度:O(nloglogn)
package acwing;
import java.util.Scanner;
public class 筛质数_普通法 {
/**
n(1+1/2+1/3+...+1/n)即循环*每一个数可能计算到概率
普通筛法O(nlgn):就是使用前面小的数,筛掉后面是它倍数的数,这样可以筛掉所有的合数,留下质数。
稍微改进后就是:埃氏筛法 O(nloglogn)约为O(n),仅使用质数筛后面的合数。这样可以保证筛掉所有的合数。
为什么是nloglogn:质数定理,一个数n,从1-n中有n/ln(n)个质数
n(1+1/2+1/3+...+1/n)即循环*每一个数可能计算到概率
n(循环次数)ln(n)(调和级数当n->无穷大时为ln(n) + C) / ln(n)少了ln(n)倍 = O(n)
*/
static int cnt = 0, N = 1000010;
static int[] primes = new int[N];
// 用于判断是否筛过
static boolean[] st = new boolean[N];
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
get_primes(n);
System.out.println(cnt);
}
private static void get_primes(int n) {
for (int i = 2; i <= n; i++) {
if (!st[i]) {
primes[cnt++] = n;
st[i] = true;
for (int j = i + i; j <= n; j = j + i) {
st[j] = true;
}
}
}
}
}
1.3.2 线性筛法
在数量比较大的时候,线性筛法比埃氏筛法快一倍
一般使用线性筛法来筛质数,但是埃氏筛法的思想比较重要,经常用来解决其他问题。
package acwing;
import java.util.Scanner;
public class 筛质数_线性筛法 {
/**
线性筛法:保证所有的合数使用它的最小质因子筛掉
为什么是线性的:每个数只有一个最小质因子,所以每个数只会被筛一次,
所以是线性的
*/
static int cnt = 0, N = 1000010;
static int[] primes = new int[N];
// 用于判断是否筛过
static boolean[] st = new boolean[N];
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
get_primes(n);
System.out.println(cnt);
}
private static void get_primes(int n) {
for (int i = 2; i <= n; i++) {
if (!st[i]) primes[cnt++] = i;
// 为什么质数>n/i的时候跳出:i是合数,会从break跳出。要保证,primes[j] * i <= n -> i除过来
for (int j = 0; primes[j] <= n / i; j++) {
/**
从小到大枚举质数
i % primes[j] == 0 primes[j]是i的最小质因子 也是primes[j] * i的最小质因子
i % primes[j] != 0 primes[j]小于i的最小质因子,也是primes[j] * i的最小质因子
无论如何,primes[j]都会是primes[j] * i的最小质因子
*/
st[primes[j] * i] = true;
if (i % primes[j] == 0) break;
}
}
}
}
2. 约数
2.1 试除法求一个数的所有约数
package acwing;
import java.util.Arrays;
import java.util.Collections;
import java.util.Scanner;
import java.util.Vector;
public class 求约数_试除法 {
public static void main(String[] args) {
/**
一个数的约数是成对出现的 n / d = x 那么d和x都是n的约数
枚举小的哪一个约数就好了
d <= n/d -> d<=sqrt(n) 时间复杂度:O(sqrt(n))
*/
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
while (n > 0) {
n--;
int x = sc.nextInt();
Vector<Integer> res = get_divisors(x);
for (int t: res) {
System.out.print(t + " ");
}
}
}
static Vector<Integer> get_divisors(int n) {
Vector<Integer> res = new Vector<>();
for (int i = 1; i <= n / i; i++) {
if (n % i == 0) {
res.add(i);
if (i != n / i) res.add(n / i);
}
}
Collections.sort(res);
return res;
}
}
2.2 约数个数
package acwing;
import java.util.HashMap;
import java.util.Map;
import java.util.Scanner;
public class 约数个数 {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
// 存储质约数和它出现的次数
Map<Integer, Integer> map = new HashMap<>();
while (n > 0) {
n--;
int x = sc.nextInt();
// 分解质因数
for (int i = 2; i <= x / i; i++) {
while (x % i == 0) {
x /= i;
if (map.containsKey(i)) {
map.put(i, map.get(i) + 1);
} else {
map.put(i, 1);
}
}
}
if (x > 1)
if (map.containsKey(x)) {
map.put(x, map.get(x) + 1);
} else {
map.put(x, 1);
}
}
double mod = 1e9 + 7;
long res = 1;
for (int t: map.keySet()) {
res = res * (map.get(t) + 1);
}
System.out.println((int) (res % mod));
}
}
2.3 约数之和
package acwing;
import java.util.HashMap;
import java.util.Map;
import java.util.Scanner;
public class 约数之和 {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
Map<Integer, Integer> map = new HashMap<>();
while (n > 0) {
n--;
int x = sc.nextInt();
for (int i = 2; i <= x / i; i++) {
while (x % i == 0) {
x /= i;
if (map.containsKey(i)) {
map.put(i, map.get(i) + 1);
} else {
map.put(i, 1);
}
}
}
if (x > 1)
if (map.containsKey(x)) {
map.put(x, map.get(x) + 1);
} else {
map.put(x, 1);
}
}
long res = 1;
double mod = 1e9 + 7;
for (int x : map.keySet()) {
int k = map.get(x);
long t = 1;
// x0-xk t = t * p + 1 -> t = (p + 1) * p + 1
while (k > 0) {
k--;
t = (long) ((t * x + 1) % mod);
}
res = (long) ((res * t) % mod);
}
System.out.println(res);
}
}
2.4 欧几里得算法(辗转相除法)
求最大公约数
package acwing;
import java.util.Scanner;
public class gcd {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
while (n > 0) {
n--;
int a, b;
a = sc.nextInt();
b = sc.nextInt();
System.out.println(gcd(a, b));
}
}
static int gcd(int a, int b) {
return b > 0 ? gcd(b, a % b) : a;
}
}