停更阶段学习算法题的一些总结
目录
- 一星题
-
- 快速排序
- 归并排序
- 高精度加法
- 高精度乘法
- 前缀和
- 子矩阵的和（二维数组的前缀和）
- 移除元素
- 二分查找
- 回文数
- 二星题目
-
- 单链表（数组模拟实现）
- 双链表(数组实现）
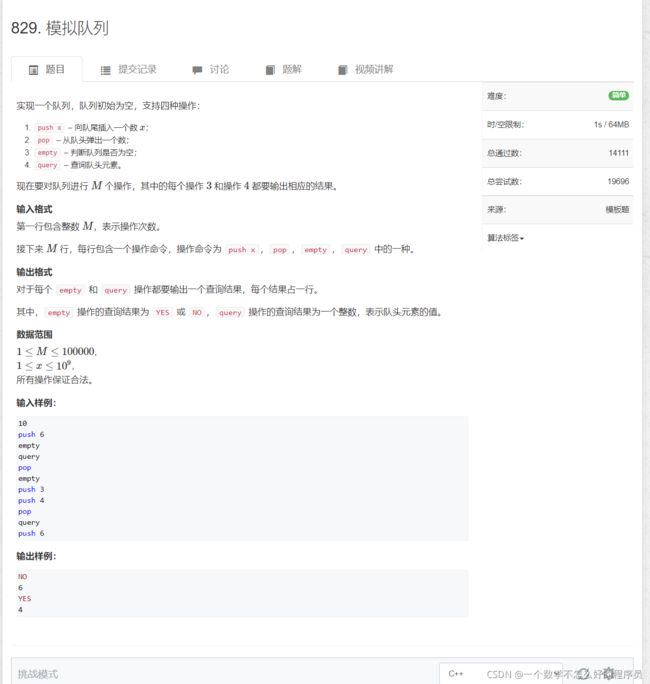
- 模拟栈
- 模拟队列
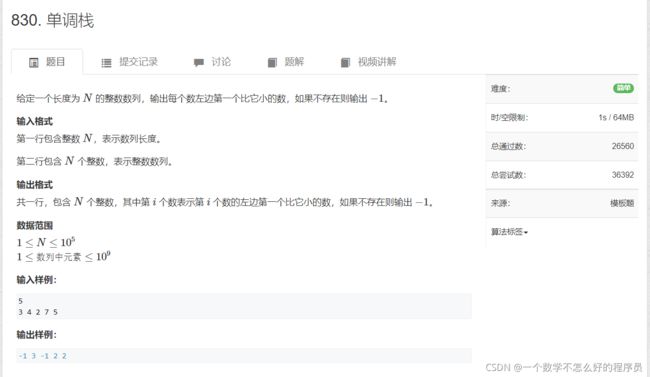
- 单调栈
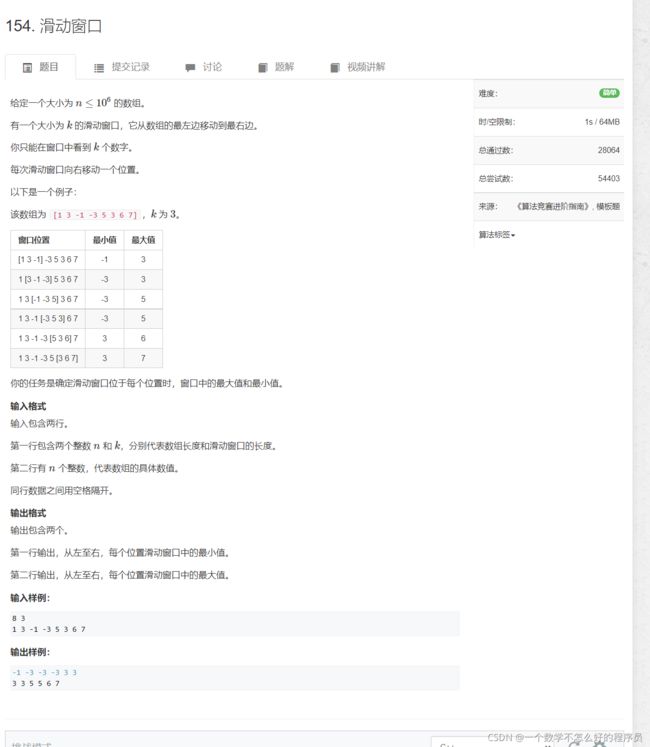
- 滑动窗口（单调队列）
- KMP算法
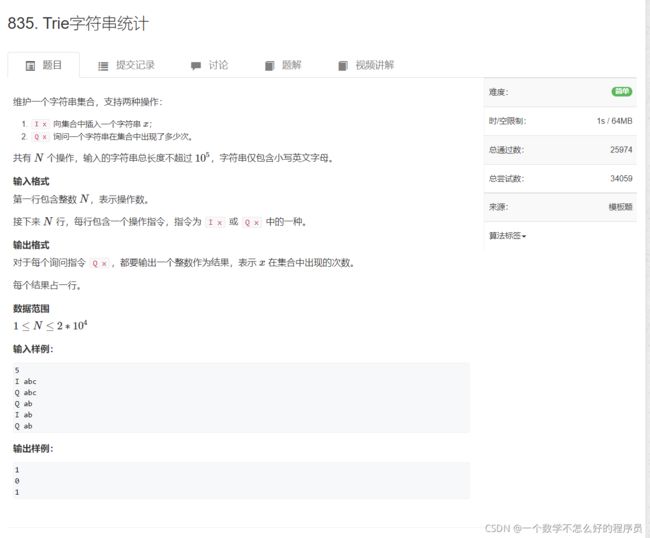
- Trie字符串统计
- 最大异或对
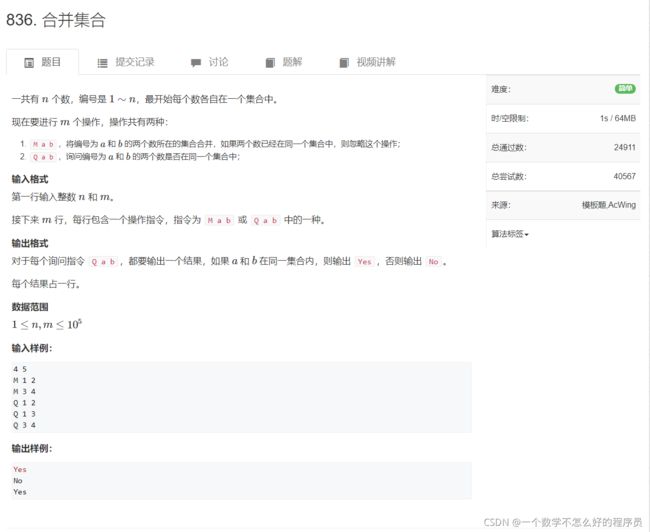
- 并查集
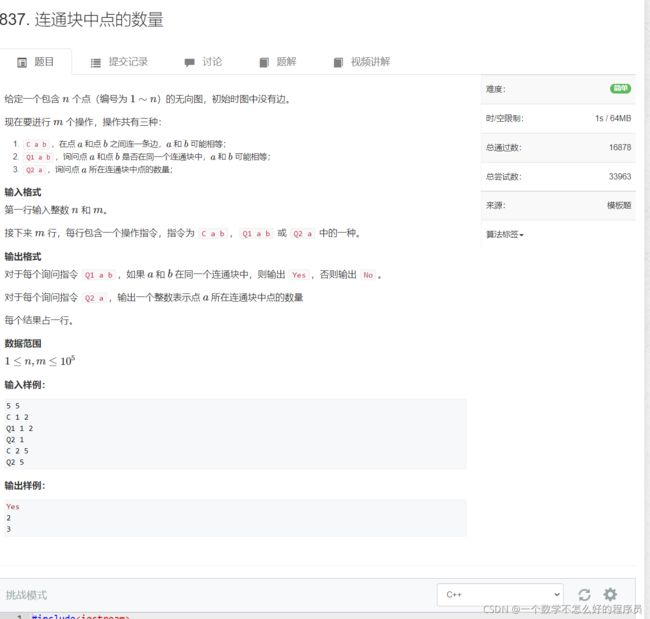
- 连通块中点的数量（并查集的应用）
- 堆排序
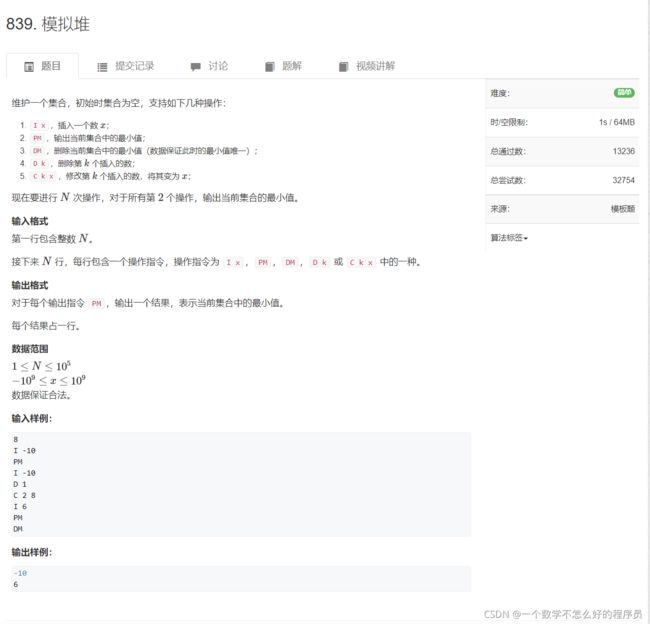
- 模拟堆
- BFS
-
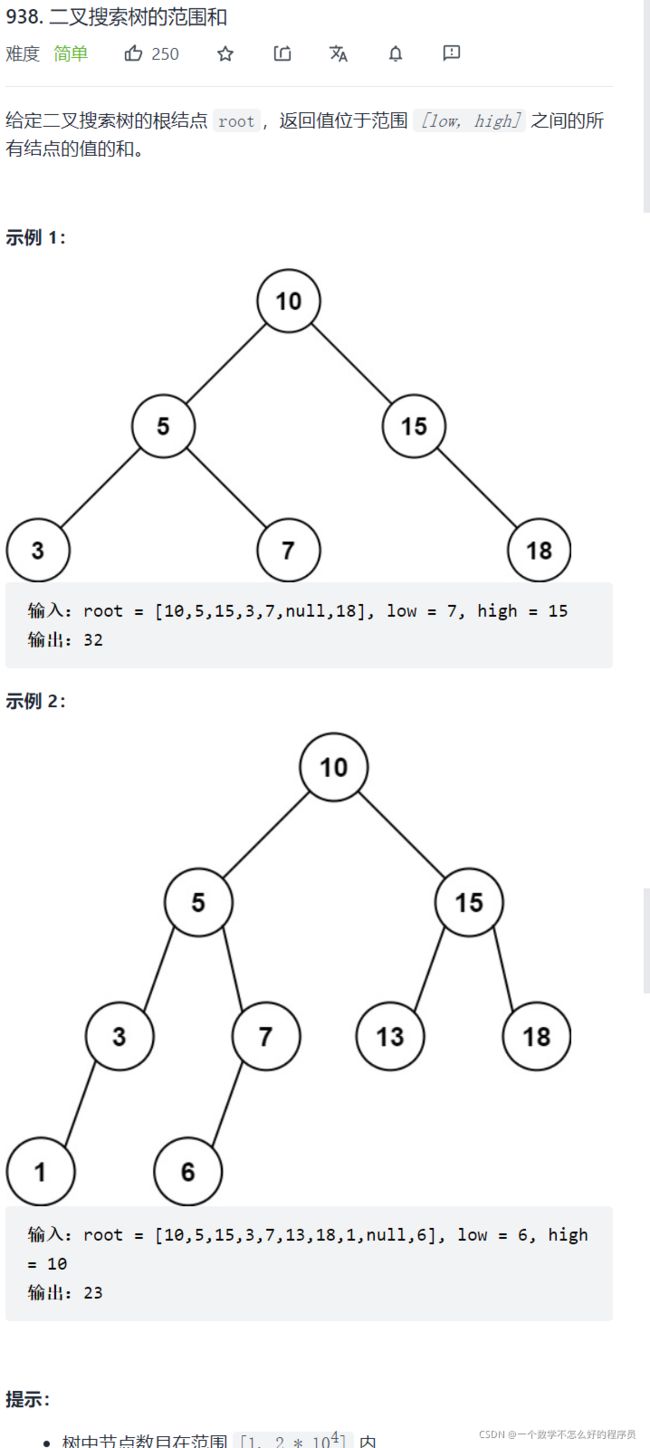
- 二叉树的范围和
- 二叉树的层序遍历II
- 岛屿数量（在下面的DFS中有出现）
- 二叉树的层序遍历
- DFS
-
- 二叉树的范围和（在上面的BFS中出现过，不再重复）
- 二叉树的层序遍历（在BFS中出现过，不再重复）
- 二叉树的中序遍历
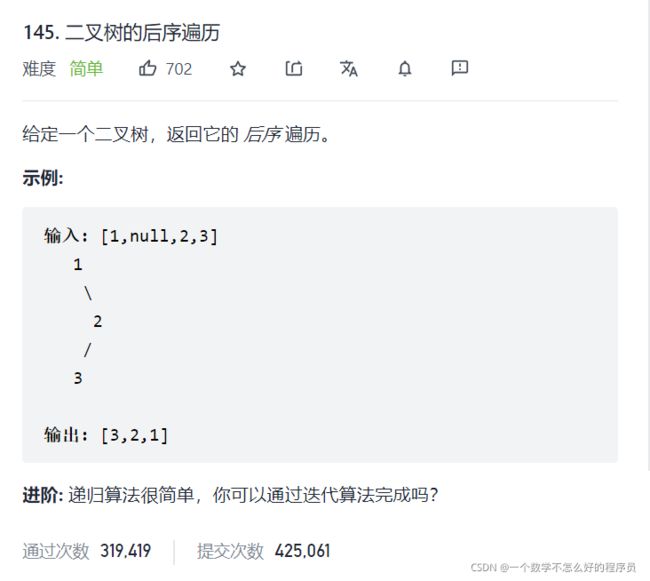
- 二叉树的后序遍历
- 括号生成
- 子集
- 全排列
- 岛屿数量
- 贪心
-
- 分发饼干
- 回溯
-
- 子集（在上面的DFS中出现过，不再重复）
- 括号生成（在上面的DFS中出现过，不再重复）
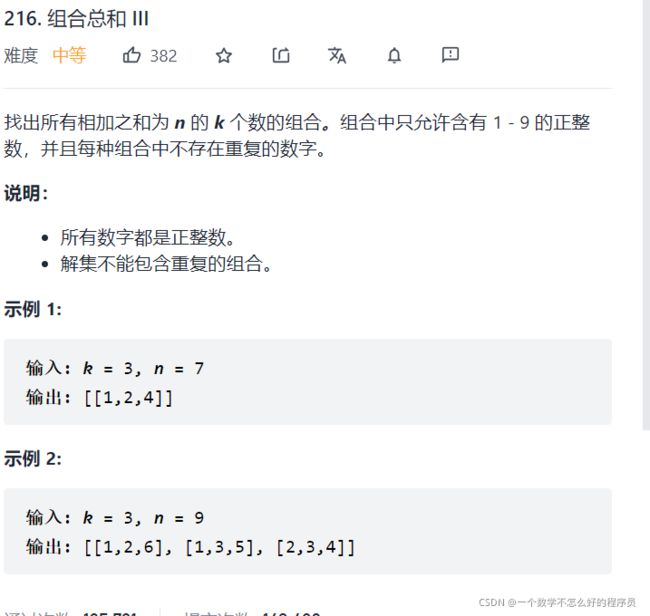
- 组合总和III
- 组合
- 哈希
-
- 快乐数（set）
- 两个数组的交集（set）
- 有效的字母异位词（数组）
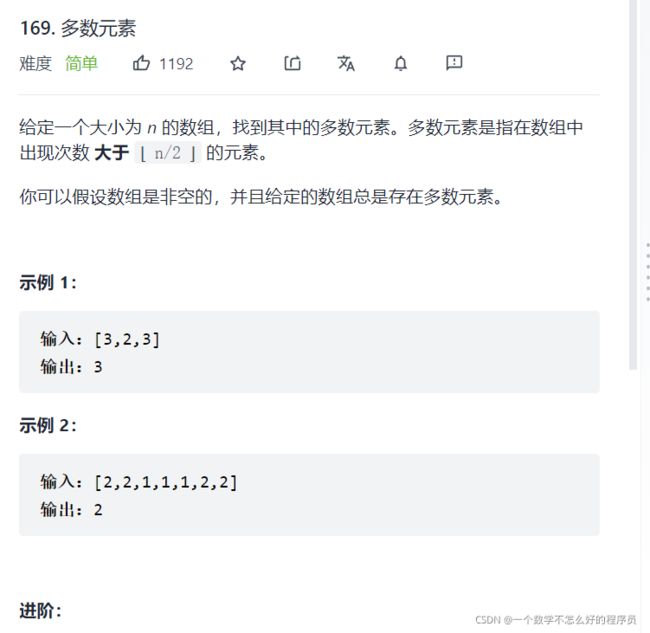
- 多数元素（数组）
- 动态规划
-
- 最大子序和
- 三级目录
一星题
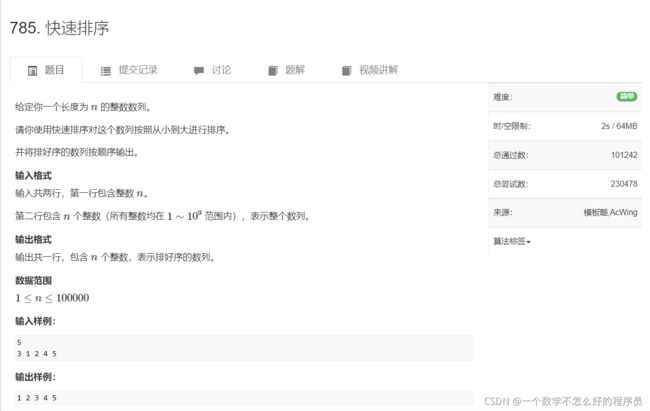
快速排序
题目链接：快速排序
其实这道题在停更之前的八大排序中已经涉及过了，下面来看看y总的代码。
#include y总的代码其实是很简便和优雅的，但由于我比较习惯之前的实现方式，所以遇到快速排序时一直都是用的我自己的那套写法。
void QuickSort1(int* a, int left, int right)
{
if (left >= right)//当只有一个数据或是序列不存在时，不需要进行操作
return;
int begin = left;//L
int end = right;//R
int key = left;//key的下标
while (left < right)
{
//right先走，找小
while (left < right&&a[right] >= a[key])
{
right--;
}
//left后走，找大
while (left < right&&a[left] <= a[key])
{
left++;
}
if (left < right)
{
swap(&a[left], &a[right]);
}
}
int meet = left;//L和R的相遇点
swap(&a[key], &a[meet]);//交换key和相遇点的值
QuickSort1(a, begin, meet - 1);//key的左序列进行此操作
QuickSort1(a, meet + 1, end);//key的右序列进行此操作
}
这只是快速排序的一种实现方法：Hoare法。其他的方法可以看这篇文章：八大排序
归并排序
题目链接：归并排序
这里也不多结束了，之前的那篇八大排序中也涉及到了此排序。
y总的代码：
#include 自己平常写的：
void MergeSort(int* a, int left, int right,int* temp)
{
if (left >= right)
return;
int mid = left + (right - left) / 2;
int begin1 = left, end1 = mid;
int begin2 = mid+1, end2 = right;
int i = left,j=0; //i一定要写成left不能写成0，如果是递归左序列还可以适用，但是递归到右序列时就不行了
MergeSort(a, left, mid, temp); //这里要注意区间的划分，不然可能出现死递归
MergeSort(a, mid + 1, right, temp);
while (begin1 <= end1&&begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
temp[i++] = a[begin1++];
}
else
{
temp[i++] = a[begin2++];
}
}
while (begin1 <= end1)
{
temp[i++] = a[begin1++];
}
while (begin2 <= end2)
{
temp[i++] = a[begin2++];
}
for (j = left; j < right + 1; j++)
{
a[j] = temp[j];
}
}
高精度加法
其实这就是一道模拟题，并不涉及什么算法，注意到细节也就相对容易了。
题目链接：高精度加法
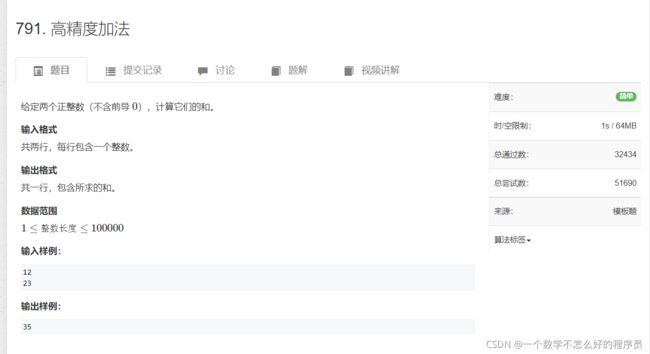
代码实现：
#include 注意：这里写代码时要时刻想清楚哪个时候vector里面存放的是正向排序，什么时候是逆序的。
由于减法其实就是加上一个负数，其实如果你愿意，也可以把减速的运算过程模拟出来，因为之前已经介绍了加法，所以减法这里就不过多介绍了。
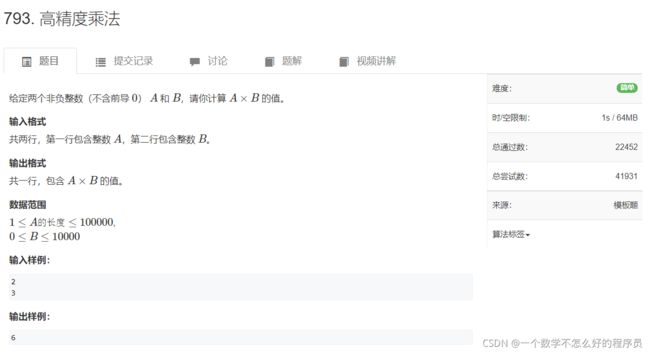
高精度乘法
题目链接：高精度乘法
代码实现：
#include 注意：乘法前导0的问题。
前缀和
题目链接：前缀和
这道题如果用暴力解法的话，时间可能会超时。但是用了前缀和的话，从O（n）的复杂度可以变为O（1）的复杂度。下面我们先来了解一下前缀和是什么，其实这和高中学的数列的知识有些关系，前缀和其实是一个S[N]的数组，其中N为元素的个数，S[1]表示a1，S[2]表示a1+a2，S[3]表示a1+a2+a3，也就是说i是几，S[i]就是前几项的和，这里我们第一个元素在数组中下标并不是从0开始的，而是从1开始的。
代码实现：
#include 如果你一开始并不能怎么看懂这段代码，其实你举一个示例，然后对着代码看，其实很容易理解。下面我们来提升一下难度，这里是一维数组的前缀和，下面看看二维数组的前缀和。
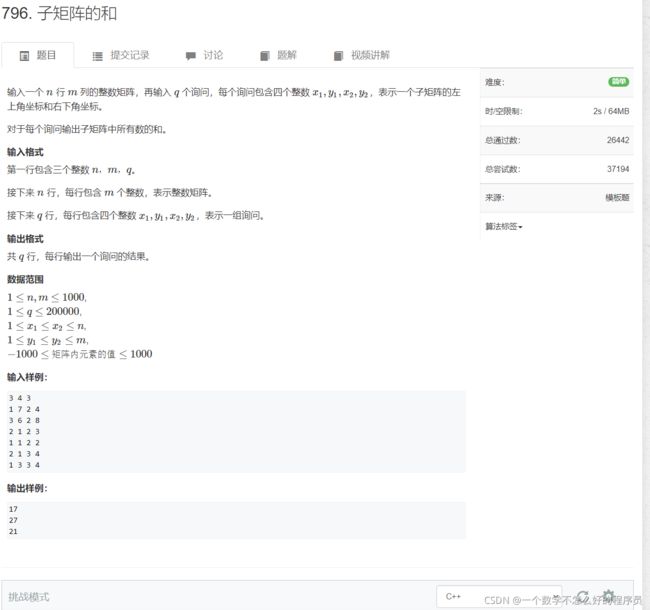
子矩阵的和（二维数组的前缀和）
题目链接：子矩阵的和
代码实现：
#include 这段代码想比前面的一维数组前缀和，难度又提升了，不过大致的思路还是一样的。这里博主就不具体介绍了，因为这只是一篇用于个人总结的博客。下面附上一张我分析时的图片。
移除元素
题目链接：移除元素
代码实现：
class Solution {
public:
int removeElement(vector<int>& nums, int val)
{
if(nums.size()==0)
{
return 0;
}
vector<int>::iterator begin=nums.begin();
vector<int>::iterator end=nums.end()-1;
while(begin<end)
{
while(begin<end&&(*begin)!=val)
{
begin++;
}
while(begin<end&&(*end)==val)
{
end--;
}
swap((*begin),(*end));
}
int sum=0;
for(vector<int>::iterator i=nums.begin();i!=nums.end();i++)
{
if((*i)!=val)
{
++sum;
}
}
return sum;
}
};
更优的做法（双指针法）：
// 时间复杂度：O(n)
// 空间复杂度：O(1)
class Solution {
public:
int removeElement(vector<int>& nums, int val) {
int slowIndex = 0;
for (int fastIndex = 0; fastIndex < nums.size(); fastIndex++) {
if (val != nums[fastIndex]) {
nums[slowIndex++] = nums[fastIndex];
}
}
return slowIndex;
}
};
二分查找
题目链接：二分查找
代码实现：
class Solution {
public:
int search(vector<int>& nums, int target)
{
int right=nums.size()-1;
int left=0;
while(left<=right)
{
int mid=left+(right-left)/2;
if(nums[mid]>target)
{
right=mid-1;
}
else if(nums[mid]<target)
{
left=mid+1;
}
else
{
return mid;
}
}
return -1;
}
};
第二种写法：
// 版本二
class Solution {
public:
int search(vector<int>& nums, int target) {
int left = 0;
int right = nums.size(); // 定义target在左闭右开的区间里，即：[left, right)
while (left < right) { // 因为left == right的时候，在[left, right)是无效的空间，所以使用 <
int middle = left + ((right - left) >> 1);
if (nums[middle] > target) {
right = middle; // target 在左区间，在[left, middle)中
} else if (nums[middle] < target) {
left = middle + 1; // target 在右区间，在[middle + 1, right)中
} else { // nums[middle] == target
return middle; // 数组中找到目标值，直接返回下标
}
}
// 未找到目标值
return -1;
}
};
回文数
题目链接：回文数
bool isPalindrome(int x){
if(x<0|(x%10==0&&x!=0))
{
return false;
}
if(x==0)
{
return true;
}
int temp=0;
int nums=0;
while(x>temp)
{
temp=temp*10+x%10;
x/=10;
}
if(temp/10==x||temp==x)
{
return true;
}
else
{
return false;
}
}
二星题目
二星题目里面的算法题基本都涉及到一些数据结构了或者是一些比较难理解的题目。
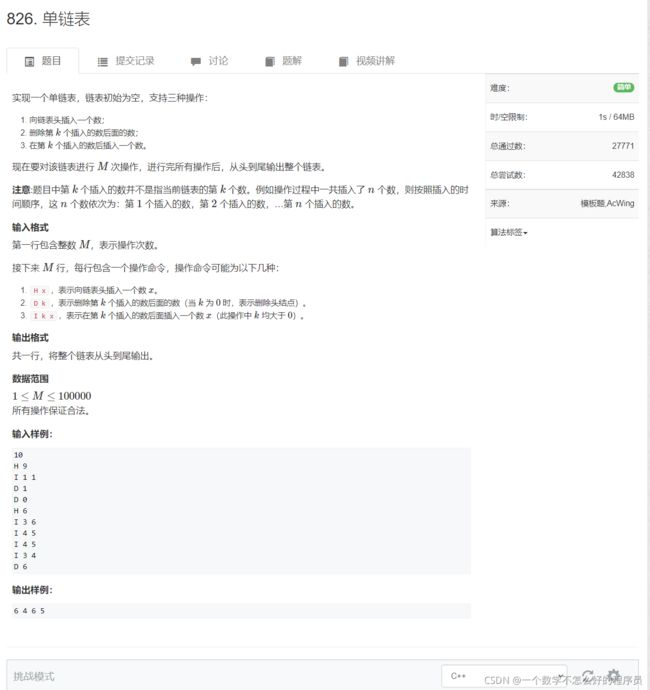
单链表（数组模拟实现）
题目链接：单链表
代码实现：
y总的代码实现：
#include 自己的代码实现：
#include如果你还是不怎么理解单链表，可以去看看博主之前关于单链表的文章。单链表的实现
双链表(数组实现）
题目链接：双链表
代码实现:
y总的：
#include 自己做时：
#include对双向带头循环不怎么了解的小伙伴可以去看看博主之前的这篇文章。双向带头循环链表的实现
模拟栈
题目链接：模拟栈
代码实现：
y总的：
#include 自己写时：
#include如果对栈不怎么熟悉的小伙伴可以去看看博主之前的这篇文章。栈的多种实现
模拟队列
题目链接：模拟队列
代码实现：
y总的：
#include 自己写时：
#include其实队列和栈的实现很像，都是用一个数组，然后用一个类似于头指针和尾指针的控制量来解决问题。
如果对队列不怎么理解的小伙伴可以去看看博主之前的这篇文章：队列的实现
单调栈
题目链接：单调栈
代码实现：
y总的：
#include 自己写时：
#include 滑动窗口（单调队列）
题目链接：滑动窗口（单调队列）
代码实现：
y总的：
#include 自己写时：
#includeKMP算法
题目链接：KMP字符串
关于KMP算法，博主之前专门写了一篇文章来介绍。KMP算法
如果看文章还不怎么懂的小伙伴可以去看看B站的这个教学视频，将的真的很清楚。KMP算法视频讲解
Trie字符串统计
题目链接：Trie字符串统计
代码实现：
y总的：
#include 自己写时：
#include
for(int i=0;str[i];i++)
{
//将a~z这些字母映射为0~26，注意是'a'而不是“a”，不然减的就不是阿斯克码了
int u=str[i]-'a';
//s这个数组表示以p为根节点的第u号儿子是否存在，如果不存在的话，则++idx，存在的话则，则迭代，此时
//让之前的儿子节点变为父亲节点。
if(!s[p][u])
{
s[p][u]=++idx;
}
p=s[p][u];
}
//cnt用于记录字符串出现的次数的，当for循环结束时，则以p根节点结束的那个分支的字符串的cnt++
cnt[p]++;
}
int query(char* str)
{
int p=0;
for(int i=0;str[i];i++)
{
int u=str[i]-'a';
if(!s[p][u])
{
return 0;
}
p=s[p][u];
}
return cnt[p];
}
int main()
{
int n;
scanf("%d",&n);
while(n--)
{
char op[2];
scanf("%s%s",op,str);
if(op[0]=='I')
{
Insert(str);
}
else
{
printf("%d\n",query(str));
}
}
return 0;
}
下面这张是我分析这段代码时画的图，如果读者不怎么看的懂这段代码，也可以举几个例子来结合代码理解。
最大异或对
题目链接：最大异或对
代码实现：
y总的：
#include 自己写时：
#include写这题时很难直接想到这个思路，所以一开始我们可以用暴力的解法去尝试一下，但时间上可能会过不去，这个时候我们想办法去优化它就行了，发现第一层for循环肯定是无法在优化了，只能想办法去优化第二层for循环了。
并查集
题目链接：并查集
代码实现：
y总的：
#include 自己写时：
#include连通块中点的数量（并查集的应用）
题目链接：连通块中点的数量
代码实现：
y总的：
#include 自己写时：
#include堆排序
关于堆排序，之前博主详细写了一篇介绍的文章。有兴趣的小伙伴可以去看看。堆排序
模拟堆
题目链接：模拟堆
代码实现：
y总的：
#include 自己写时：
#include说实话模拟堆的意思并不是很大，所以看不懂也没有太大的问题。
BFS
注意：往往BFS能做的题，DFS也能做出来，反之亦然，所以下面的题目可能在DFS或者BFS有重复的情况
二叉树的范围和
题目链接：二叉树的范围和
代码实现：
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
/*
//用前序遍历的方法，遍历过程中如果满足条件就加到sum上（这个其实也能看成是dfs）
class Solution {
public:
int rangeSumBST(TreeNode* root, int low, int high)
{
int sum=0;
BinaryPrev(root,low,high,sum);
return sum;
}
void BinaryPrev(TreeNode* n1, int low, int high,int& sum)
{
if(n1==NULL)
{
return;
}
if (n1!=NULL&&n1->val>=low&&n1->val<=high)
{
sum+=n1->val;
}
if(n1!=NULL)
{
BinaryPrev(n1->left,low,high,sum);
BinaryPrev(n1->right,low,high,sum);
}
}
};*/
/*
//递归法（其实就是dfs）：整个树满足要求的节点和==左子树满足要求的节点和+右子树满足要求的节点和+根节点是否满足
class Solution {
public:
int rangeSumBST(TreeNode* root, int low, int high)
{
int sum=func(root,low,high);
return sum;
}
int func(TreeNode* root, int low, int high)
{
int sum=0;
/*if(root==NULL)
{
return 0;
}
else
{
//计算左子树所有满足要求的节点和
int leftsum=func(root->left,low,high);
//计算右子树所有满足要求的节点和
int rightsum=func(root->right,low,high);
//最后看根节点是否满足要求，满足则加
if(root->val>=low&&root->val<=high)
{
sum=leftsum+rightsum+root->val;
}
else
{
sum=leftsum+rightsum;
}
}*/
/*
//换种写法
if(root==NULL)
{
return 0;
}
int leftsum=func(root->left,low,high);
int rightsum=func(root->right,low,high);
sum=leftsum+rightsum;
if(root->val>=low&&root->val<=high)
{
sum=leftsum+rightsum+root->val;
}
return sum;
}
};
*/
//bfs算法解决 广度优先遍历，一层一层的看，满足则加。一般bfs算法都要结合队列解决问题
class Solution {
public:
int rangeSumBST(TreeNode* root, int low, int high)
{
queue<TreeNode*> q;
int sum=func(root,low,high,q);
return sum;
}
int func(TreeNode* root, int low, int high,queue<TreeNode*>& q)
{
int sum=0;
if(root!=NULL)
{
q.push(root);
}
/*while(q.size()>0)
{
//这个里面的while循环是用来处理当前这一层的节点的
while(q.size()>0)
{
TreeNode* cur=q.front();
if(cur->val>=low&&cur->val<=high)
{
sum+=cur->val;
}
if(cur->left!=NULL)
{
q.push(cur->left);
}
if(cur->right!=NULL)
{
q.push(cur->right);
}
//你这人pop时其实size就已经减过了，所以没有必要再size--了
q.pop();
//--q.size();
}
}*/
//更加好的写法
while(!q.empty())
{
int count=q.size();
for(int i=0;i<count;i++)
{
TreeNode* cur=q.front();
if(cur->val>=low&&cur->val<=high)
{
sum+=cur->val;
}
if(cur->left!=NULL)
{
q.push(cur->left);
}
if(cur->right!=NULL)
{
q.push(cur->right);
}
q.pop();
}
}
return sum;
}
};
二叉树的层序遍历II
题目链接：二叉树的层序遍历II
代码实现：
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
//bfs算法
class Solution {
public:
int Max(int a, int b)
{
return a > b ? a : b;
}
int maxDepth(struct TreeNode* root)
{
if (root == NULL)
{
return 0;
}
return 1 + Max( maxDepth(root->left), maxDepth(root->right));
}
vector<vector<int>> levelOrderBottom(TreeNode* root)
{
vector<vector<int>> res;
int depth=maxDepth(root);
res.resize(depth);
queue<TreeNode*> q;
if(root==NULL)
{
return res;
}
q.push(root);
while(!q.empty())
{
int size=q.size();
vector<int> cur;
for(int i=0;i<size;i++)
{
TreeNode* temp=q.front();
q.pop();
cur.push_back(temp->val);
if(temp->left!=NULL)
{
q.push(temp->left);
}
if(temp->right!=NULL)
{
q.push(temp->right);
}
}
res[depth-1]=cur;
depth--;
}
return res;
}
};
岛屿数量（在下面的DFS中有出现）
二叉树的层序遍历
题目链接：二叉树的层序遍历
代码实现：
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
//bfs算法
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root)
{
vector<vector<int>> res;
queue<TreeNode*> q;
if(root==NULL)
{
return res;
}
q.push(root);
/*
while(!q.empty())
{
vector cur;
int count=q.size();
while(count>0)
{
TreeNode* node=q.front();
//q.pop();
cur.push_back(node->val);
if(node->left!=NULL)
{
q.push(root->left);
}
if(node->right!=NULL)
{
q.push(root->right);
}
count--;
}
res.push_back(cur);
}*/
//这样写不容易写出bug来，而且代码更加的优美好理解
while(!q.empty())
{
int size=q.size();
vector<int> cur;
for(int i=0;i<size;i++)
{
TreeNode* temp=q.front();
q.pop();
cur.push_back(temp->val);
if(temp->left!=NULL)
{
q.push(temp->left);
}
if(temp->right!=NULL)
{
q.push(temp->right);
}
}
res.push_back(cur);
}
return res;
}
};
//dfs的方法，其实就是用先序遍历来做这一题
/*class Solution {
public:
vector> levelOrder(TreeNode* root)
{
vector> res;
if(root==NULL)
{
return res;
}
else
{
dfs(res,root,0);
}
return res;
}
void dfs(vector>& res,TreeNode* root,int level)
{
if(root==NULL)
{
return;
}
//如果res中不够用，就插入一个数组
if(level>=res.size())
{
//注意这儿往里面插入括号的写法
res.push_back(vector ());
}
res[level].push_back(root->val);
if(root->left!=NULL)
{
dfs(res,root->left,level+1);
}
if(root->right!=NULL)
{
dfs(res,root->right,level+1);
}
}
};*/
DFS
二叉树的范围和（在上面的BFS中出现过，不再重复）
二叉树的层序遍历（在BFS中出现过，不再重复）
二叉树的中序遍历
题目链接：二叉树的中序遍历
代码实现：
typedef struct TreeNode BT;
int BinarySize(BT* root)
{
return root==NULL ? 0:BinarySize(root->left)+BinarySize(root->right)+1;
}
void MiddleOrder(BT* root,int* arr,int* pi)
{
if(root)
{
MiddleOrder(root->left,arr,pi);
arr[(*pi)++]=root->val;
MiddleOrder(root->right,arr,pi);
}
}
int* inorderTraversal(struct TreeNode* root, int* returnSize){
int size=BinarySize(root);
int i=0;
int *arr=(int*)malloc(sizeof(int)*size);
MiddleOrder(root,arr,&i);
*returnSize=size;
return arr;
}
二叉树的后序遍历
题目链接：二叉树的后序遍历
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
/**
* Note: The returned array must be malloced, assume caller calls free().
*/
int BinarySize(struct TreeNode* root)
{
if(root==NULL)
{
return 0;
}
else
{
return BinarySize(root->left)+BinarySize(root->right)+1;
}
}
void AfterOrder(struct TreeNode* root,int *arr,int* pi)
{
if (root == NULL)
{
return;
}
AfterOrder(root->left,arr,pi);
AfterOrder(root->right,arr,pi);
arr[(*pi)++]=root->val;
}
int* postorderTraversal(struct TreeNode* root, int* returnSize){
int size=BinarySize(root);
int *arr=(int *)malloc(sizeof(int)*size);
int i=0;
AfterOrder(root,arr,&i);
*returnSize=size;
return arr;
}
括号生成
题目链接：括号生成
代码实现：
class Solution {
public:
vector<string> generateParenthesis(int n)
{
vector<string> res;
backtracking(n,res,0,0,"");
return res;
}
void backtracking(int n,vector<string>& res,int leftnums,int rightnums,string str)
{
if(rightnums>leftnums)
{
return ;
}
if(leftnums<n)
{
//str.add('(');
backtracking(n,res,leftnums+1,rightnums,str+"(");
//str.pop_back();
}
if(rightnums<leftnums)
{
backtracking(n,res,leftnums,rightnums+1,str+")");
}
if(leftnums==n&&rightnums==n)
{
res.push_back(str);
return;
}
}
};
/*
// DFS深度优先搜索算法来解决
class Solution {
public:
vector res; //记录答案
vector generateParenthesis(int n) {
dfs(n , 0 , 0, "");
return res;
}
void dfs(int n ,int lc, int rc ,string str)
{
if( lc == n && rc == n)
{
res.push_back(str); //递归边界
return ;
}
else
{
if(lc < n) dfs(n, lc + 1, rc, str + "("); //拼接左括号
if(rc < n && lc > rc) dfs(n, lc, rc + 1, str + ")"); //拼接右括号
}
}
};
*/
子集
题目链接：子集
代码实现：
//回溯算法
/*class Solution {
public:
vector> subsets(vector& nums)
{
vector> res;
vector sub;
//注意这儿集合的写法，必须要写成{}
res.push_back({});
//for循环每次子集的长度
for(int length=1;length<=nums.size();length++)
{
//传res是因为back这个函数是void返回类型的，所以我们要将其传入，在函数里面改变它
//length是用来记录这个子集的长度的
//0这个位置的参数表示我们下一次要访问的元素
//sub这个数组存储这个子集
backtracking(nums,res,length,0,sub);
}
return res;
}
void backtracking(vector& nums,vector>& res,int length,int idx,vector& sub)
{
//当sub这个数组的长度达到要求的长度时就将这个子集插入到结果集中
if(sub.size()==length)
{
res.push_back(sub);
return ;
}
for(int i=idx;i
//dfs算法
class Solution {
public:
vector<vector<int>> subsets(vector<int>& nums)
{
vector<vector<int>> res;
vector<int> sub;
dfs(nums,res,0,sub);
return res;
}
void dfs(vector<int>& nums,vector<vector<int>>& res,int idx,vector<int>& sub)
{
//注意这个要每次写在dfs的最开头，这个和回溯算法看起来很像，但还是有区别的，因为你去画树形图
//时，他每一个节点其实就是一个集合。所以这句话要写在一开头，具体可以看图解。
res.push_back(sub);
if(idx==nums.size())
{
//res.push_back(sub);
return ;
}
for(int i=idx;i<nums.size();i++)
{
sub.push_back(nums[i]);
dfs(nums,res,i+1,sub);
sub.pop_back();
}
}
};
全排列
题目链接：全排列
代码实现：
class Solution {
public:
vector<vector<int>> permute(vector<int>& nums)
{
vector<vector<int>> ans;
vector<int> array;
vector<bool> st=vector<bool>(nums.size());
dfs(ans,array,nums,st);
return ans;
}
void dfs(vector<vector<int>>& ans,vector<int>& array,vector<int> nums,vector<bool>& st)
{
if(array.size()==nums.size())
{
ans.push_back(array);
return;
}
for(int i=0;i<nums.size();i++)
{
if(!st[i])
{
array.push_back(nums[i]);
st[i]=true;
dfs(ans,array,nums,st);
array.pop_back();
st[i]=false;
}
}
}
};
y那儿写的：
#include回溯的写法：
class Solution {
public:
vector<vector<int>> result;
vector<int> path;
void backtracking (vector<int>& nums, vector<bool>& used) {
// 此时说明找到了一组
if (path.size() == nums.size()) {
result.push_back(path);
return;
}
for (int i = 0; i < nums.size(); i++) {
if (used[i] == true) continue; // path里已经收录的元素，直接跳过
used[i] = true;
path.push_back(nums[i]);
backtracking(nums, used);
path.pop_back();
used[i] = false;
}
}
vector<vector<int>> permute(vector<int>& nums) {
result.clear();
path.clear();
vector<bool> used(nums.size(), false);
backtracking(nums, used);
return result;
}
};
岛屿数量
题目链接：岛屿数量
代码实现：
/*
//dfs同化方法
class Solution {
public:
int numIslands(vector>& grid)
{
int res=func(grid);
return res;
}
int func(vector>& grid)
{
if(grid.size()==0)
{
return 0;
}
int sum=0;
//注意c++中二维数组行和列的计算
int row=grid.size();
int col=grid[0].size();
int i=0,j=0;
for(i=0;i>& grid,int x,int y,int row,int col)
{
//首先写出递归的结束条件
if(x<0||y<0||x>=row||y>=col||grid[x][y]=='0')
{
return ;
}
//首先把当前位置弄成0
grid[x][y]='0';
//接下来dfs他的前后左右
dfs(grid,x+1,y,row,col);
dfs(grid,x-1,y,row,col);
dfs(grid,x,y+1,row,col);
dfs(grid,x,y-1,row,col);
}
};
*/
//bfs算法
/*
class Solution {
public:
int numIslands(vector>& grid)
{
int res=func(grid);
return res;
}
int func(vector>& grid)
{
if(grid.size()==0)
{
return 0;
}
queue> q;
int sum=0;
//注意c++中二维数组行和列的计算
int ROW=grid.size();
int COL=grid[0].size();
int i=0,j=0;
for(i=0;i0)
{
auto cur=q.front();
q.pop();
int x=cur.first,y=cur.second;
//检查此元素上面一个元素
if(x-1>=0&&grid[x-1][y]=='1')
{
grid[x-1][y]='0';
q.push({x-1,y});
}
//检查下面一个元素
if(x+1=0&&grid[x][y-1]=='1')
{
grid[x][y-1]='0';
q.push({x,y-1});
}
//检查右边一个元素
if(y+1
//并查集的写法
class UnionFind
{
public:
vector<int> root;
//用来记录合并的次数的
int count=0;
//构造函数
UnionFind(vector<vector<char>>& grid)
{
int row=grid.size();
int col=grid[0].size();
//总共的个数
count=row*col;
for(int i=0;i<row*col;i++)
{
root.push_back(i);
}
}
int find(int x)
{
if(x!=root[x])
{
root[x]=find(root[x]);
}
return root[x];
}
void unite(int x,int y)
{
int rootx=find(x);
int rooty=find(y);
if(rootx!=rooty)
{
root[rootx]=rooty;
//此时合并了一个，总的count就减一
count--;
}
}
int getCount()
{
return count;
}
};
class Solution {
public:
int numIslands(vector<vector<char>>& grid)
{
//4个方向的方向向量
int dx[4] = {-1,1,0,0};
int dy[4] = {0,0,-1,1};
if(grid.size()==0)
{
return 0;
}
int row=grid.size();
int col=grid[0].size();
//记录有多少个水域
int water=0;
//将二维数组grid传入并查集这个类中，构成并查集
UnionFind uf(grid);
for(int i=0;i<row;i++)
{
for(int j=0;j<col;j++)
{
if(grid[i][j]=='0')
{
water++;
}
else
{
//检查4个方向，能同化则同化
for(int k=0;k<4;k++)
{
int x=i+dx[k];
int y=j+dy[k];
if(x>=0&&y>=0&&x<row&&y<col&&grid[x][y]=='1')
{
//这里面有一个二维数组下标转化成一维数组下标的问题
uf.unite(x*col+y,i*col+j);
}
}
}
}
}
//最终答案=总的个数-0（水域的个数）-联通的次数
return uf.getCount()-water;
}
};
贪心
分发饼干
题目链接：分发饼干
代码实现：
class Solution {
public:
/*int findContentChildren(vector& g, vector& s)
{
sort(g.begin(),g.end());
sort(s.begin(),s.end());
int cnt=0;
vector flags;
flags.resize(s.size(),false);
for(int i=0;i=g[i]&&flags[j]==false)
{
++cnt;
flags[j]=true;
break;
}
}
}
return cnt;
}*/
//贪心算法
int findContentChildren(vector<int>& g, vector<int>& s)
{
sort(g.begin(),g.end());
sort(s.begin(),s.end());
int cnt=0;
int tempj=s.size()-1;
/*for(int i=g.size()-1;i>=0;i--)
{
for(int j=tempj;j>=0;j--)
{
if(s[j]>=g[i])
{
++cnt;
tempj=j-1;
break;
}
}
}*/
//一个for循环的写法
int indexs=s.size()-1;
for(int i=g.size()-1;i>=0;i--)
{
if(indexs>=0&&s[indexs]>=g[i])
{
++cnt;
--indexs;
}
}
return cnt;
}
};
回溯
子集（在上面的DFS中出现过，不再重复）
括号生成（在上面的DFS中出现过，不再重复）
组合总和III
题目链接：组合总和III
代码实现：
class Solution {
public:
vector<vector<int>> res;
vector<int> path;
vector<vector<int>> combinationSum3(int k, int n)
{
int sum=0;
backtracking(sum,n,k,1);
return res;
}
void backtracking(int sum,int n,int k,int c)
{
if(path.size()==k)
{
if(sum==n)
{
res.push_back(path);
}
return ;
}
for(int i=c;i<=9;i++)
{
sum+=i;
path.push_back(i);
backtracking(sum,n,k,i+1);
sum-=i;
path.pop_back();
}
}
};
组合
题目链接：组合
代码实现：
/*class Solution {
public:
vector> combine(int n, int k)
{
vector> res;
vector cur;
dfs(res,cur,n,k);
return res;
}
void dfs(vector>& res,vectorcur,int n,int k)
{
if(cur.size()==k)
{
res.push_back(cur);
return;
}
//这样倒着写在这题中是有好处的，可以少传一个参数进来，具体可以看此题图解。
for(int i=n;i>=1;i--)
{
cur.push_back(i);
//注意这边一定是i-1，因为你要的是这个元素的之前一个元素。
dfs(res,cur,i-1,k);
//同样回头时不要忘了pop
cur.pop_back();
}
}
};*/
/*
//for循环中正过来的写法
class Solution {
public:
vector> combine(int n, int k)
{
vector> res;
vector cur;
//这时要多传入一个变量，不然解决不了问题，具体看此题图解
int curn=1;
dfs(res,cur,n,k,curn);
return res;
}
void dfs(vector>& res,vectorcur,int n,int k,int curn)
{
if(cur.size()==k)
{
res.push_back(cur);
return;
}
for(int i=curn;i<=n;i++)
{
cur.push_back(i);
//注意这边一定是i+1，因为你要的是这个元素的之后一个元素。
dfs(res,cur,n,k,i+1);
//同样回头时不要忘了pop
cur.pop_back();
}
}
};*/
//回溯写法
class Solution {
public:
vector<vector<int>> res;
vector<int> path;
vector<vector<int>> combine(int n, int k)
{
backtracking(n,k,1);
return res;
}
void backtracking(int n,int k,int startindex)
{
if(path.size()==k)
{
res.push_back(path);
return;
}
for(int i=startindex;i<=n;i++)
{
path.push_back(i);
backtracking(n,k,i+1);
path.pop_back();
}
}
};
哈希
快乐数（set）
题目链接：快乐数
代码实现：
class Solution {
public:
// 取数值各个位上的单数之和
int getSum(int n) {
int sum = 0;
while (n) {
sum += (n % 10) * (n % 10);
n /= 10;
}
return sum;
}
bool isHappy(int n) {
unordered_set<int> set;
while(1) {
int sum = getSum(n);
if (sum == 1) {
return true;
}
// 如果这个sum曾经出现过，说明已经陷入了无限循环了，立刻return false
if (set.find(sum) != set.end()) {
return false;
} else {
set.insert(sum);
}
n = sum;
}
}
};
两个数组的交集（set）
题目链接：两个数组的交集
代码实现：
class Solution {
public:
vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {
unordered_set<int> result_set; // 存放结果
unordered_set<int> nums_set(nums1.begin(), nums1.end());
for (int num : nums2) {
// 发现nums2的元素 在nums_set里又出现过
if (nums_set.find(num) != nums_set.end()) {
result_set.insert(num);
}
}
return vector<int>(result_set.begin(), result_set.end());
}
};
有效的字母异位词（数组）
题目链接：有效的字母异位词
代码实现：
class Solution {
public:
bool isAnagram(string s, string t) {
int record[26] = {0};
for (int i = 0; i < s.size(); i++) {
// 并不需要记住字符a的ASCII，只要求出一个相对数值就可以了
record[s[i] - 'a']++;
}
for (int i = 0; i < t.size(); i++) {
record[t[i] - 'a']--;
}
for (int i = 0; i < 26; i++) {
if (record[i] != 0) {
// record数组如果有的元素不为零0，说明字符串s和t 一定是谁多了字符或者谁少了字符。
return false;
}
}
// record数组所有元素都为零0，说明字符串s和t是字母异位词
return true;
}
};
多数元素（数组）
题目链接：多数元素
代码实现：
/* 排序法
class Solution {
public:
int majorityElement(vector& nums)
{
sort(nums.begin(), nums.end());
return nums[nums.size() / 2];
}
};
*/
/*分治法
class Solution {
public:
int majorityElement(vector& nums)
{
return getmajor(nums,0,nums.size()-1);
}
int getmajor(vector& nums,int left,int right)
{
if (left == right)
{
return nums[left];
}
int mid = (left+right) / 2;
int left_majority = getmajor(nums, left, mid);
int right_majority = getmajor(nums, mid + 1, right);
if(left_majority==right_majority)
{
return left_majority;
}
int leftcount=0;
int rightcount=0;
for(int i=left;i<=right;i++)
{
if(nums[i]==left_majority)
{
leftcount++;
}
if(nums[i]==right_majority)
{
rightcount++;
}
}
return leftcount>=rightcount?left_majority:right_majority;
}
};
*/
/*哈希法
class Solution {
public:
int majorityElement(vector& nums)
{
unordered_map hash;
for(int i=0;inums.size()/2)
{
return it.first;
}
}
return 0;
}
};
*/
动态规划
最大子序和
题目链接：最大子序和
代码实现：
/*暴力法，时间上面是过不去
class Solution {
public:
int maxSubArray(vector& nums)
{
int n=nums.size();
int max=INT_MIN;
for(int i=0;imax)
{
max=sum;
}
}
}
return max;
}
};
*/
/*分治法
class Solution {
public:
int maxSubArray(vector& nums)
{
return getmax(nums,0,nums.size()-1);
}
int threemax(int a, int b, int c)
{
if (a>b)
{
if (c>a)
{
return c;
}
else
{
return a;
}
}
else
{
if (b > c)
{
return b;
}
else
{
return c;
}
}
}
int getmax(vector& nums,int left,int right)
{
if(left==right)
{
return nums[left];
}
int mid=left+(right-left)/2;
int leftmax=getmax(nums,left,mid);
int rightmax=getmax(nums,mid+1,right);
int crossmax=midmax(nums,left,right);
return threemax(leftmax,rightmax,crossmax);
}
int midmax(vector& nums,int left,int right)
{
if(left==right)
{
return nums[left];
}
int mid=left+(right-left)/2;
int maxleft=nums[mid];
int sumleft=nums[mid];
int maxright=nums[mid+1];
int sumright=nums[mid+1];
for(int i=mid-1;i>=left;i--)
{
sumleft+=nums[i];
if(sumleft>maxleft)
{
maxleft=sumleft;
}
}
for(int i=mid+2;i<=right;i++)
{
sumright+=nums[i];
if(sumright>maxright)
{
maxright=sumright;
}
}
return maxleft+maxright;
}
};*/
/*动态规划
class Solution {
public:
int max(int a,int b)
{
return a>b?a:b;
}
int maxSubArray(vector& nums)
{
int n=nums.size();
vector dp;
dp.resize(n,0);
dp[0]=nums[0];
int maxdp=nums[0];
for(int i=1;imaxdp)
{
maxdp=dp[i];
}
}
return maxdp;
}
};*/