算法学习记录～2023.5.16～贪心Day1～455.分发饼干 & 376. 摆动序列 & 53. 最大子序和

基础知识

1. 什么是贪心算法

贪心的本质是选择每一个阶段的局部最优，从而达到全局最优

需要满足的条件可以抽象为满足以下条件：

• 最优子结构：规模较大的问题的解由规模较小的子问题的解组成，规模较大的问题的解只由其中一个规模较小的子问题的解决定
• 无后效性：后面阶段的求解不会修改前面阶段已经计算好的结果
• 贪心选择性质：从局部最优解可以得到全局最优解

正例：
Q：有一堆钞票，可以拿走十张，如果想达到最大的金额，要怎么拿？
A：每次拿最大的，最终结果就是拿走最大数额的钱

反例（不符合应用场景）：
Q：如果是有一堆盒子，你有一个背包体积为n，如何把背包尽可能装满
A：如果还每次选最大的盒子，就不行了。涉及到下一章的动态规划。

2. 贪心的套路（什么时候用贪心）

并没有固定套路来判定就是要用贪心算法。

最好用的策略是举反例，如果想不到反例就可以试一试贪心算法。

刷题或者面试的时候，手动模拟一下感觉可以局部最优推出整体最优，而且想不到反例，那么就试一试贪心。
很多时候都很像靠常识。

3. 贪心一般解题步骤

一般分为如下四步：

1. 将问题分解为若干个子问题
2. 找出适合的贪心策略
3. 求解每一个子问题的最优解
4. 将局部最优解堆叠成全局最优解

其实做题时候没像回溯三步曲一样严格，只要想清楚局部最优是什么，如果推导出全局最优，其实就够了。

---

455.分发饼干

题目链接

力扣题目链接

思路

先将两个数组都排序，从小到大。

这里的局部最优就是小饼干喂给胃口小的，充分利用饼干尺寸喂饱一个，全局最优就是喂饱尽可能多的小孩

按需求从小到大依次遍历，针对每一个需求再从最小饼干开始遍历找符合要求的最小一个，接着把坐标移到该饼干之后（因为之后的需求只会更大，因此前面的肯定都不符合了）继续遍历。

代码

class Solution {
public:
    int findContentChildren(vector<int>& g, vector<int>& s) {
        sort(g.begin(), g.end());
        sort(s.begin(), s.end());
        //vector used(s.size(), 1);      //如果还有就是1，被分了就是0
        int result = 0;
        int cur = 0;            //记录当前饼干位置
        for (int i = 0; i < g.size(); i++){     //从最小需求开始，找符合要求的最小饼干
            for (int j = cur; j < s.size(); j++){
                if (s[j] >= g[i]){
                    result ++;
                    cur = j + 1;        //从符合要求的下一个开始
                    break;              //已经找到符合要求的最小饼干，不需要继续遍历
                }
            }
        }

        return result;
    }
};

总结

比较简单的思路，注意break位置的用法

---

376. 摆动序列

题目链接

力扣题目链接

思路1：直接遍历暴力求解（可能也算贪心）

一开始把题目理解成了寻找符合摆动序列的最长连续子序列，完全偏离了题意。
本题意思其实是要求从一整个序列中抽取符合摆动序列的元素组成的子序列的长度，并不需要连续。

因此直观思路就是从开头到结尾遍历，定义一个状态来记录子序列中前两个数的差的正负，如果后面遇到正负相反的数说明找到了下一个节点，依次累加即可。

这个其实很符合直觉。它没有记录具体的变化的点，也因此省去了很多思考和处理过程，因为只要数值的上升（下降）趋势发生变化那自然就是发生了摆动，记录下这个摆动即可。
如果需要记录具体的节点则需要像思路2一样具体考虑各种情况，以及取舍和删除等问题。

代码

class Solution {
public:
    int wiggleMaxLength(vector<int>& nums) {
        int state = 0;      //用于记录子序列中前两个节点的大小关系。1则说明之前差为正，-1说明差为负
        int result = 0;     //最终结果
        for (int i = 1; i < nums.size(); i++){      //需要 i - 1 所以从1开始而不是0
            if (nums[i] > nums[i - 1] && state != 1){   //当前差为正且前一个状态差为负。使用 ！= 可以兼容初始化的0
                result ++;
                state = 1;
            }
            else if (nums[i] < nums[i - 1] && state != -1){     //当前差为负且前一个状态差为正。使用 ！= 可以兼容初始化的0
                result ++;
                state = -1;
            }
        }
        return result + 1;      //result是两两比较出来的，因此实际个数要加一个边界值1
    }
};

思路2：正经贪心（其实只是考虑的更具体一点）

大致思路和1其实差不多，这个可能考虑的更细一点。

要考虑三种情况：

1. 上下坡中有平坡
2. 数组首尾两端
3. 单调坡中有平坡

处理好这三种情况即可，具体根据代码注释来看比较好。

情况1：上下坡中有平坡

比如下图所示，这种情况可以统一规则删除最左（最右也行）的 n - 1 个，这样 prediff = 0 && curdiff < 0 也就是平坡最右发生状态变化时也需要记录一个峰值。
所以记录峰值的条件是 (preDiff <= 0 && curDiff > 0) || (preDiff >= 0 && curDiff < 0)
（讲的是思维过程，其实这里还不完全能解决，还需要讨论完剩下两种情况）

情况2：数组首尾两端

当只有两个元素时可以写死，也可以像下面一样融入通用判断规则。

可以假设，数组最前面还有一个数字，那这个数字应该是什么呢？

之前我们在 讨论 情况1 的时候， prediff = 0 ，curdiff < 0 或者 >0 也记为波谷。
那么为了规则统一，针对序列[2,5]，可以假设为[2,2,5]，这样它就有坡度了即preDiff = 0，如图：

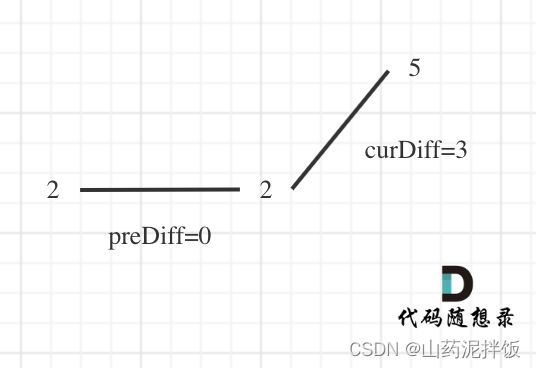
针对以上情形，result初始为1（默认最右面有一个峰值），此时curDiff > 0 && preDiff <= 0，那么result++（计算了左面的峰值），最后得到的result就是2（峰值个数为2即摆动序列长度为2）

由上面两种情况讨论可以得出下面代码（其实还欠缺了情况3的处理）

class Solution {
public:
    int wiggleMaxLength(vector<int>& nums) {
        if (nums.size() <= 1) return nums.size();
        int curDiff = 0; // 当前一对差值
        int preDiff = 0; // 前一对差值
        int result = 1;  // 记录峰值个数，序列默认序列最右边有一个峰值
        for (int i = 0; i < nums.size() - 1; i++) {
            curDiff = nums[i + 1] - nums[i];
            // 出现峰值
            if ((preDiff <= 0 && curDiff > 0) || (preDiff >= 0 && curDiff < 0)) {
                result++;
            }
            preDiff = curDiff;
        }
        return result;
    }
};

情况3：单调坡度有平坡

刚才版本代码忽略了单调坡度有平坡的情况

图中，我们可以看出，刚才的代码在三个地方记录峰值，但其实结果因为是2，因为 单调中的平坡 不能算峰值（即摆动）。

之所以会出问题，是因为我们实时更新了 prediff。

事实上，我们只需要在 这个坡度 摆动变化的时候，更新prediff就行，这样prediff在 单调区间有平坡的时候 就不会发生变化，造成我们的误判。

修改一下prediff更新的位置即可。

所以最终代码如下面的代码所示

代码

class Solution {
public:
    int wiggleMaxLength(vector<int>& nums) {
        if (nums.size() <= 1) return nums.size();
        int curDiff = 0; // 当前一对差值
        int preDiff = 0; // 前一对差值
        int result = 1;  // 记录峰值个数，序列默认序列最右边有一个峰值
        for (int i = 0; i < nums.size() - 1; i++) {
            curDiff = nums[i + 1] - nums[i];
            // 出现峰值
            if ((preDiff <= 0 && curDiff > 0) || (preDiff >= 0 && curDiff < 0)) {
                result++;
                preDiff = curDiff; // 注意这里，只在摆动变化的时候更新prediff 
            }
        }
        return result;
    }
};

思路3：动态规划

完成下一章节动态规划后再补

总结

不知道为什么感觉凭直觉做其实又快又准，一定要按照carl哥教程来反而觉得麻烦了很多…
不过就当考虑事情更周全的思维锻炼好了。

---

53. 最大子序和

题目链接

力扣题目链接

思路1：暴力for循环

暴力解法的思路，第一层 for 就是设置起始位置，第二层 for 循环遍历数组寻找最大值

时间复杂度：O(n^2)
空间复杂度：O(1)

当然这个作为medium的题目这么做在leetcode上是无法通过的，会超时

代码

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int result = INT32_MIN;
        int sum;                //初始和
        for (int i = 0; i < nums.size(); i++){
            sum = 0;            //针对每一个数为起点的初始和
            for (int j = i; j < nums.size(); j++){  //注意为i开始
                sum += nums[j];
                if (sum > result)
                    result = sum;
            }
        }
        return result；
    }
};

思路2：贪心

用一个sum来求当前的连续和。
基本思想在遍历求和时，如果当前的连续和为负数，那么后面无论加什么值都只会更小，因此为了求最大子序列和，连续和需要保持大于等于0，这样再继续加后面的才有可能继续增大。如果连续和已经为负数，那就清空连续和重新开始计算，因为这时候带上原来的元素只会更小，不如从新开始。
结合图解

具体实现结合下面代码来看

时间复杂度：O(n)
空间复杂度：O(1)

代码

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int sum = 0;                //当前连续和
        int result = INT_MIN;       //结果。初始化为最小值
        for (int i = 0; i < nums.size(); i++){
            sum += nums[i];
            result = sum > result ? sum : result;   //不断更新最大值
            if (sum < 0)            //连续和为负数时就重新开始计算
                sum = 0;
        }
        return result;
    }
};

思路3：动态规划

完成下一章节动态规划后再补

总结

一开始还想用回溯法做一下，有的用例可以过有的不可以，花了很久手动实操以后发现问题在于通过回溯方式做的话，并不是连续的序列，这就是错误原因。

---