【刷题日记】贪心算法

分配问题

leetcode 455 分发饼干

假设你是一位很棒的家长，想要给你的孩子们一些小饼干。但是，每个孩子最多只能给一块饼干。
对每个孩子 i，都有一个胃口值 g[i]，这是能让孩子们满足胃口的饼干的最小尺寸；并且每块饼干 j，都有一个尺寸 s[j] 。如果 s[j] >= g[i]，我们可以将这个饼干 j 分配给孩子 i ，这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子，并输出这个最大数值。

思路

每个孩子只有一块饼干。
饥饿度最小的孩子最容易满足，最节省饼干。
为了尽可能满足数量多的孩子，应优先满足最不饿的孩子。

代码

def findContentChildre(g,s):
	g = sorted(g)
	s = sorted(s)
	ch = 0, co =0 # 从左到右遍历
	while( g[ch]<len(g) and s[co]<len(s)):
		if (g[ch] <= s[co]): # ch号孩子可以被co号饼干满足
			ch+=1  # 可以被满足的孩子多一个
		co+=1 # 否则看下一块饼干能不能满足这个孩子
	return ch

leetcode 135 分发糖果

老师想给孩子们分发糖果，有 N 个孩子站成了一条直线，老师会根据每个孩子的表现，预先给他们评分。
你需要按照以下要求，帮助老师给这些孩子分发糖果：
每个孩子至少分配到 1 个糖果。
评分更高的孩子必须比他两侧的邻位孩子获得更多的糖果。
那么这样下来，老师至少需要准备多少颗糖果呢？

输入：一个数组，表示孩子的评分
输出：最少糖果的数量

思路

先让每个孩子的右边满足评分高的人得到多一个的糖果
再让每个孩子的左边满足多一个糖果的要求
一共进行两次遍历
贪心策略：每次遍历只考虑一侧最优，比较一侧的大小关系并根据要求更新

代码

def candy(ratings):
	size = lend(ratings)
	# 如果只有一个孩子，只需要一颗糖
	if size == 1:
		return size
	# 首先给每个人分一颗糖
	candies = [1 for i in range(size))
	# 从左往右遍历到倒数第二个人
	for i in range(size - 1):
		# 初始状态都是1，只需要比较得分不需要比较糖果数量
		if ratings[i+1]>ratings[i]:
			candies[i+1] = candies[i]+1 # 右边=左边+1
	i = size-1
	# 从右向左遍历到第二个人 i = size-1 ~ 1
	while(i>0):
		# 如果左边的人得分高，但糖果没有更多
		if (ratings[i-1]>ratings[i]) and candies[i-1] <=1 candies[i]):
		candies[i-1]=candies[i]+1
		i-=1
	'''
	# for循环长这样
	for i in range(size-1):
    	if(ratings[size-1-i] < ratings[size-1-i-1] and candy[size-1-i]>=candy[size-1-i-1] ):
    	candy[size-1-i-1] = candy[size-1-i]+1
	'''
	return sum(candies) # 返回糖果总数	

435 不重叠的区间

给定一个区间的集合，找到需要移除区间的最小数量，使剩余区间互不重叠。
注意:
可以认为区间的终点总是大于它的起点。
区间 [1,2] 和 [2,3] 的边界相互“接触”，但没有相互重叠

思路

因为要移除区间的最小数量，留下更多的区间
类似于如何排更多的课是按课程的结束时间排序，然后将重叠部分去掉

ps：那么如果要移除最多的区间呢？

代码

class Solution:
    def eraseOverlapIntervals(self, intervals: List[List[int]]) -> int:
        size = len(intervals) #对输入数组做一些统计：排序啊，个数，频率，第一次出现位置，最后一次出现位置等之类的通常都会用到
        # 边界测试
        if size == 0 or size == 1:
            return 0
		#用python内置sorted函数对嵌套的list根据元素list的第二个元素从小到大排序
        intervals = sorted(intervals,key = lambda p:p[1])
        
        total = 0 # 计数器
        # 首先比较第一个区间结尾和第二个区间开头
        head = 1  # 第二个区间开头
        tail = intervals[0][1] # 第一个区间结尾
        # 从第二个区间开始遍历区间头
        while head < size:
            if intervals[head][0] < tail: # 如果重叠
                total += 1 # 该区间需要被移除
            else:
                tail = intervals[head][1] # 否则保留该区间并将区间结尾指针移到当前区间
            head+=1
        return total

605 种花问题 easy？？

假设有一个很长的花坛，一部分地块种植了花，另一部分却没有。可是，花不能种植在相邻的地块上，它们会争夺水源，两者都会死去。
给你一个整数数组 flowerbed 表示花坛，由若干 0 和 1 组成，其中 0 表示没种植花，1 表示种植了花。另有一个数 n ，能否在不打破种植规则的情况下种入 n 朵花？能则返回 true ，不能则返回 false。
示例：
输入：flowerbed = [1,0,0,0,1], n = 1
输出：true

注意还有输入是
[0], 1;
[1], 0;
[1], 1
这种

最直接的思路

遍历
第一个位置：检查当前位置和下一个位置是不是0
最后一个位置：检查当前位置和前一个位置是不是0
中间的位置：检查当前位置和前后位置是不是0
满足条件则种花。
需要标记种花的位置

需要注意的是要检查边界：
只有一个位置的情况，不然数组索引就会越界

遍历完成则计算出种花总数，和要求n比较即可
也可以在种花过程中比较，当花种够了就返回True

class Solution:
    def canPlaceFlowers(self, flowerbed: List[int], n: int) -> bool:
        size = len(flowerbed)
        if size == 0 and n>0:
            return False
        if size == 1:
            if n ==0 :
                return True
            if n == 1 and flowerbed[0] ==0:
                return True
            return False
        '''
        num_0 = 0 
        for item in flowerbed:
            if item == 0 :
                num_0 +=1
        if n > num_0/2:
            return False
        '''
        num = 0 # 记录种花数
        # 开始种花花
        # 遍历数组
        for i in range(size):
        	# 头和尾
            if (i == 0 and flowerbed[i] == 0 and flowerbed[i+1] ==0) or (i == size-1 and flowerbed[i] == 0 and flowerbed[i-1] ==0):
                num+=1
                flowerbed[i] =1
            else:
            	# 中间位置
                if flowerbed[i]==0 and flowerbed[i-1]==0 and flowerbed[i+1]==0:
                    num+=1
                    flowerbed[i]= 1

        if n > num:
            return False
        else:
            return True

但是其实这样判断边界很麻烦，容易出错，最好让边界对这个问题没有影响。
因为首尾只需要判断一边，在首尾前后都加一个0（无效位置），则既不影响结果，而且原首尾判断条件可以跟其他位置相同：
判断每个有效位置两边是不是0，都是0则种花（置1）

class Solution:
    def canPlaceFlowers(self, flowerbed: List[int], n: int) -> bool:
    	size - len(flowerbed)
    	flowerbed = [0] + flowerbed +[0]
    	num = 0 
    	for i in range(1,size+1):
    		if flowerbed[i]==0 and flowerbed[i+1]==0 and flowerbed[i-1] ==0:
    			flowerbed[i] = 1
    			num+=1
    		if num>=n:
    			return True
    	return False

763 划分字母区间

字符串 S 由小写字母组成。我们要把这个字符串划分为尽可能多的片段，同一字母最多出现在一个片段中。返回一个表示每个字符串片段的长度的列表。

示例：
输入：S = “ababcbacadefegdehijhklij”
输出：[9,7,8]
解释：
划分结果为 “ababcbaca”, “defegde”, “hijhklij”。
每个字母最多出现在一个片段中。
像 “ababcbacadefegde”, “hijhklij” 的划分是错误的，因为划分的片段数较少。

思路

这个问题的关建是每个字母的最远索引。
leetcode题解里面的一张图解非常清楚：

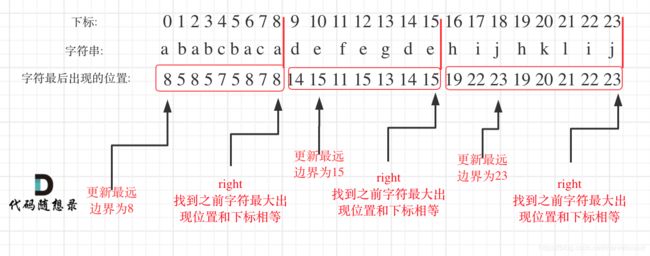
（1）记录每个字母的最远下标——用字典
（2）重新遍历字符串
a. 记住已遍历字符的最远下标
b. 如果遍历到当前字符的最远位置，且刚好是已遍历的字符的最远下标，则是分割点。

代码

class Solution:
    def partitionLabels(self, S: str) -> List[int]:
    	size = len(S)
    	# 记录每个字母最远位置
    	d= {} #一个空字典
    	for i in range(size):
    		d[S[i]] = i #根据遍历字母下标更新键值
    	
    	result = []
    	left = 0 # 切割字符串左边七点
    	right = d[S[0]]# 初始最远下标
		# 重新遍历数组
		for i in range(size):
			if d[S[i]]> right: # 如果遍历字母的最后下标大于当前最远，则更新最远下标
				right = d[S[i]}
			# 如果当前遍历是字母的最后下标且等于当前最远下标
			if i = d[S[i]] == right:
				result.append(right-left+1) #切割，字符串长度为right-left+1
				left = right+1 # 更新左端起点到切割点右方
		return result