二叉树遍历详解(递归遍历、非递归栈遍历,Morris遍历)
一、前言
《二叉查找树全面详细介绍》中讲解了二叉树操作:搜索(查找)、遍历、插入、删除。其中遍历深度优先遍历(DFS)按照实现方法可以分为:递归遍历实现、非递归遍历实现、Morris遍历实现,文中只给了代码,没有对实现过程进行讲解,本文将对递归遍历实现、非递归遍历栈实现、Morris遍历实现这三类实现方法进行讲解。
二、三类实现方法特点
递归实现
- 编码简单,易于理解;
- 隐式使用栈存储当前没有处理完的节点信息;
- 若树深度大,递归深度大可能会超过堆栈保留大小;
时间复杂度:O(n),空间复杂度:O(logn)
非递归栈实现
- 显示使用栈存储当前没有处理完的节点信息,需要花费额外时间来维护栈并为栈留出空间;
- 若树结构不是理想结构(呈线性)栈可能需要保存树中几乎所有节点信息,当树很大的时候这会是一个严重问题;
- 效率相对递归实现会高一些,实现起来会比递归实现复杂一些;
时间复杂度:O(n),空间复杂度:O(logn)
Morris遍历
- 占用空间少,不用额外花费时间维护栈和为栈留出空间;
- 利用了树中空节点;
- 实现复杂,理解有一定难度;
时间复杂度:O(n),空间复杂度:O(1)
三、递归遍历实现
递归深度遍历是最常见的写法,也最好理解,直接看代码。
// 前序遍历,递归实现
template
void BST::preorder(BSTNode* p)
{
if (p != 0)
{
visit(p);
preorder(p->m_left);
preorder(p->m_right);
}
}
// 中序遍历,递归实现
template
void BST::inorder(BSTNode* p)
{
if (p != 0)
{
inorder(p->m_left);
visit(p);
inorder(p->m_right);
}
}
// 后序遍历,递归实现
template
void BST::postorder(BSTNode* p)
{
if (p != 0)
{
postorder(p->m_left);
postorder(p->m_right);
visit(p);
}
} 四、非递归遍历实现
4.1 前序遍历,非递归栈实现
4.1.1 实现步骤
- 起始将树根节点添加到栈中;
- 栈弹出一个元素,访问该节点,并将该节点的右子节点和左子节点添加到栈中。说明,节点为空不用添加;
- 判断栈是否为空,为空树遍历结束,不为空继续步骤2。
4.1.2 实例演示
栈的变化过程
4.1.3 编码实现
// 前序遍历,非递归栈实现
template
void BST::iterativePreorder()
{
Stack*> travStack;
BSTNode* p = root;
if (p != 0)
{
travStack.push(p);
while (!travStack.empty())
{
p = travStack.pop();
visit(p);
if (p->m_right != 0)
travStack.push(p->m_right);
if (p->m_left != 0)
travStack.push(p->m_left);
}
}
} 4.2 中序遍历,非递归栈实现
4.2.1 实现步骤
中序遍历,非递归栈实现,提供了两种方法,思路差不多,做了一些改动,方法一iterativeInorder是《C++数据结构与算法》中提供的实现方法;方法二iterativeInorder_2,做了一些改动,思想是一样的,个人认为方法二更好一点点,这里实现步骤和思路演示用的是方法二。
- 将树根节点赋值给变量p;
- 循环判断p是否为空,非空执行循环;
- 循环中将p节点添加到栈中,访问p节点的左节点,非空就添加到栈中,继续访问p节点左节点的左节点非空就添加到栈中,直到左节点为空;
- 弹出栈顶元素将其赋值给p,并访问该元素;
- 栈不为空且弹出的栈顶元素没有右节点,继续弹出栈元素并访问它直到,栈为空或者弹出的节点有右节点;
- 将最后一个弹出的节点右节点赋值给p,回到步骤2,继续执行;
4.2.2 实例演示
栈的变化过程
4.2.3 编码实现
// 中序遍历,非递归栈实现
template
void BST::iterativeInorder()
{
Stack*> travStack;
BSTNode* p = root;
while (p != nullptr)
{
while (p != nullptr)
{
if (p->m_right)
travStack.push(p->m_right);
travStack.push(p);
p = p->m_left;
}
p = travStack.pop();
while (!travStack.empty() && p->m_right == nullptr)
{
visit(p);
p = travStack.pop();
}
visit(p);
if (!travStack.empty())
p = travStack.pop();
else
p = nullptr;
}
}
// 中序遍历,非递归栈实现
template
void BST::iterativeInorder_2()
{
Stack*> travStack;
BSTNode* p = root;
while (p != nullptr)
{
travStack.push(p);
for (; p != nullptr && p->m_left != nullptr; p = p->m_left)
travStack.push(p->m_left);
p = travStack.pop();
visit(p);
while (!travStack.empty() && p->m_right == nullptr)
{
p = travStack.pop();
visit(p);
}
p = p->m_right;
}
} 4.3 后序遍历,非递归栈实现
和中序遍历非递归栈实现有些类似,不同的是:
中序遍历弹出左节点之后,继续弹出父节点,然后判断父节点是否有右节点,没有继续弹出下一个节点;有则以这个右节点为节点进行下一次循环遍历。
后序遍历弹出左节点之后,继续弹出父节点,然后判断父节点是否有右节点,没有继续弹出下一个节点;有右节点且这个右节点之前已经访问过,继续弹出下一个节点;有右节点且这个右节点之前没有访问过,则以这个右节点为节点进行下一次循环遍历。
最主要的是需要理解当一个节点的右节点已经被访问了,则它的右节点不需要再被访问。
4.3.1 实现步骤
- 将树根节点赋值给变量p,定义一个标记变量guard将根节点赋值给它;
- 循环判断p是否为空,非空执行循环;
- 循环中将p节点添加到栈中,访问p节点的左节点,非空就添加到栈中,继续访问p节点左节点的左节点非空就添加到栈中,直到左节点为空;
- 将p赋值给guard,弹出栈顶元素将其赋值给p,并访问该元素;
- 栈不为空且弹出的栈顶元素没有右节点或者有右节点但该右节点和guard相等(也就是右节点刚刚被访问过),继续弹出栈元素并访问它直到,栈为空或者弹出的节点有右节点且没有被访问;
- 将最后一个弹出的节点右节点赋值给p,回到步骤2,继续执行
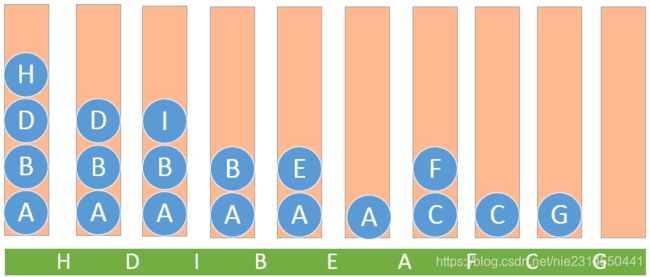
4.3.2 实例演示
栈的变化过程
说明:在栈变化过程中的第四个栈,栈顶是D,在对D节点右访问的时候,发现节点I已经被访问过,此时不需要再访问D的右节点,直接输出D节点并弹出D节点即可。
4.3.3 编码实现
// 后序遍历,非递归栈实现
template
void BST::iterativePostorder()
{
Stack*> travStack;
BSTNode* p = root, * guard = root;
while (p != nullptr)
{
for (; p->m_left != nullptr; p = p->m_left)
travStack.push(p);
while (p->m_right == nullptr || p->m_right == guard)
{
visit(p);
if (travStack.empty())
return;
guard = p;
p = travStack.pop();
}
travStack.push(p);
p = p->m_right;
}
}
五、Morris遍历
利用空闲节点找到回去的路,和避免走重复的路。
5.1 前序遍历,Morris遍历算法实现
5.1.1 实现步骤
- 将树根节点赋值给变量p;
- 若p节点没有左节点,输出p节点,并将p指向它的右节点
- 若p节点有左节点,找到p的左节点中最后访问节点(temp)
- 若temp节点右节点为空,temp的右节点指向p节点,输出p节点,并将p指向它的左节点
- 若temp节点右节点不为空,temp的右节点设置为空(恢复原始状态),输出p节点,并将p指向它的右节点
- 会到步骤2
5.1.2 实例演示
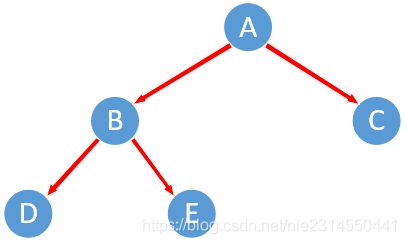
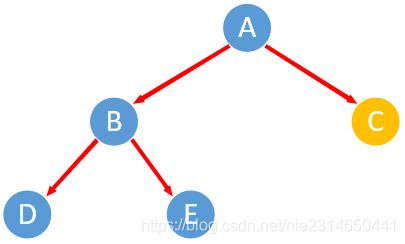
1) 树结构如下:
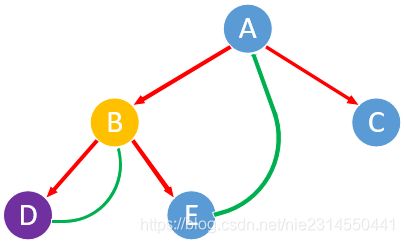
2)p指向节点A,A左节点中最后访问节点是E,将E的指向A,输出节点A。p指向A左节点B。
3)p指向节点B,B左节点中最后访问节点是D,将D的指向B,输出节点B。p指向B左节点D。
4)p指向节点D,D没左节点,输出节点D,p指向D右节点B。
5)p指向节点B,B左节点中最后访问节点是D,由于D的右节点指向B,说明D节点已经被访问了,不需要重复访问,恢复指针状态,将D的右指针设置为空。p指向B的右节点E。
6)p指向节点E,E没有左节点,输出节点E,p指向E的右节点A。
说明:这里E没有左右节点,如果有左右节点处理过程和A节点是一样的。
7)p指向节点A,A左节点中最后访问节点是E,由于E的右节点指向A,说明A节点已经被访问了,不需要重复访问,恢复指针状态,将E的右指针设置为空。p指向A的右节点C。过程同5。
8)p指向节点C,C有左节点,输出节点C,p指向C的右节点,p为空遍历结束。
5.1.3 编码实现
// 前序遍历,非递归Morris遍历算法实现
template
void BST::MorrisPreorder()
{
BSTNode* p = root, * tmp;
while (p != nullptr)
{
if (p->m_left == nullptr)
{
visit(p);
p = p->m_right;
}
else
{
tmp = p->m_left;
while (tmp->m_right != nullptr && tmp->m_right != p)
tmp = tmp->m_right;
if (tmp->m_right == nullptr)
{
visit(p);
tmp->m_right = p;
p = p->m_left;
}
else
{
tmp->m_right = nullptr;
p = p->m_right;
}
}
}
}
5.2 中序遍历,Morris遍历算法实现
5.2.1 实现步骤
和前序遍历,Morris遍历算法类似,只是输出节点顺序有一些变动。直接看代码
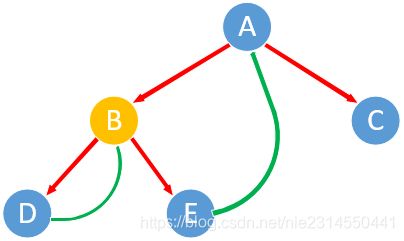
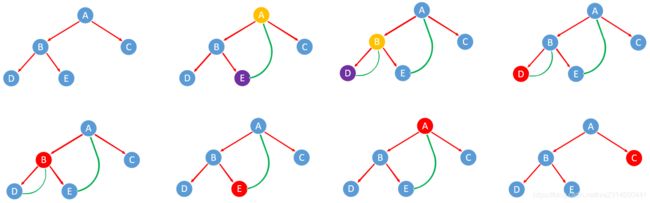
5.2.2 实例演示
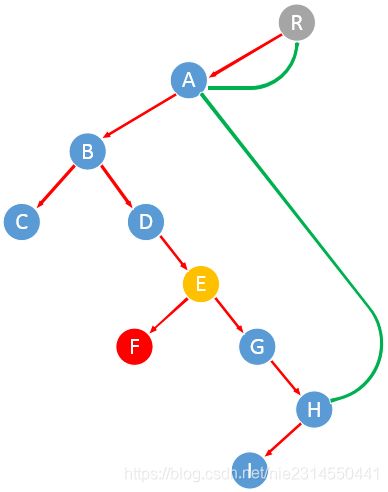
演示的图和前序是一样的,只是输出的节点顺序不一样,如下图红色点为输出的节点。
5.2.3 编码实现
// 中序遍历,非递归Morris遍历算法实现
template
void BST::MorrisInorder()
{
BSTNode* p = root, * tmp;
while (p != 0)
{
if (p->m_left == nullptr)
{
visit(p);
p = p->m_right;
}
else
{
tmp = p->m_left;
while (tmp->m_right != 0 && tmp->m_right != p)
tmp = tmp->m_right;
if (tmp->m_right == nullptr)
{
tmp->m_right = p;
p = p->m_left;
}
else
{
visit(p);
tmp->m_right = nullptr;
p = p->m_right;
}
}
}
} 5.3 中序遍历,Morris遍历算法实现
5.3.1 实现步骤
直接看演示图和代码吧,有点复杂,需要细看,图细解!
5.3.2 实例演示
约定:对于有左节点的父节点,我们需要找到父节点的左节点,并沿着这个左节点一直找它的右节点直到叶子节点为止,然后将右节点指向起始的父节点,这个最右节点查找等价于,查找一颗二叉搜索左节点中最大的一个节点。有点绕,后面需要用到,直接看下面图解就很容易理解。
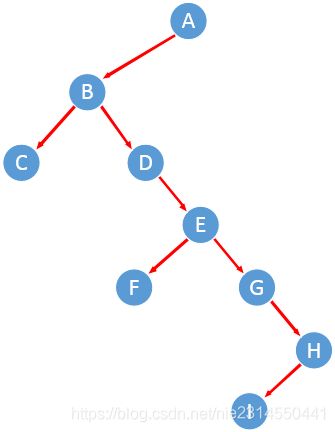
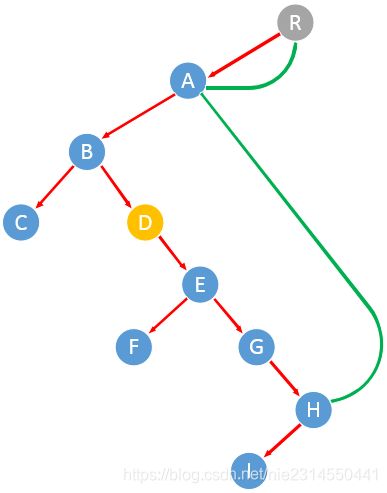
1)待遍历的树
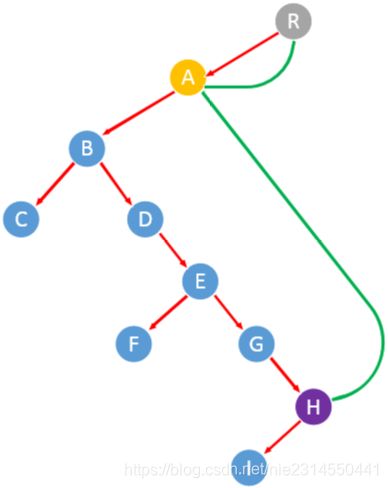
2)新加一个节点,它的左节点指向树的根节点。新加节点是为了能在遍历的规则下输出树根节点。
3)p指向节点R,p的左节点中最大的节点是A,将A的右节点指向R,p指向R节点的左节点A。
4)p指向节点A,A的左节点中最大的节点是H,将H的右节点指向A,p指向A节点的左节点B。
5)p指向节点B,B的左节点中最大的节点是C,将C的右节点指向B,p指向B节点的左节点C。
6) p指向节点C,C没有左节点,p指向C节点的右节点B。
7) p指向节点B,B节点的左节点是C,C右节点指向了B自己,输出节点C,p指向B节点的右节点D
8)p指向节点D,D没有左节点,P指向D的右节点E。
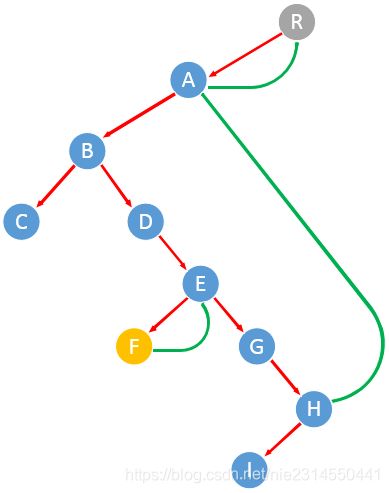
9)p指向节点E,E的左节点中最大的节点是F,将F的右节点指向E,p指向E节点的左节点F。
10)p指向节点F,F没有左节点,p指向F节点的右节点E。
11) p指向节点E,E节点的左节点是F,F右节点指向了E自己,输出节点F,p指向E节点的右节点G
12)p指向节点G,G没有左节点,P指向G的右节点H。
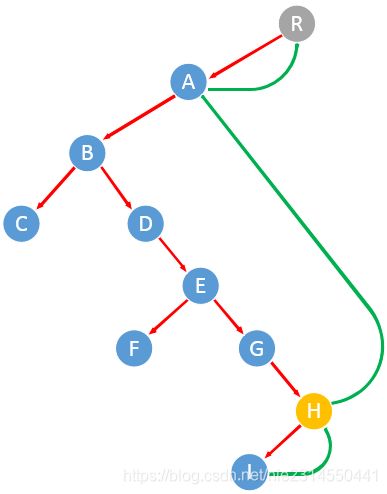
13)p指向节点H,H的左节点中最大的节点是I,将I的右节点指向H,p指向H节点的左节点I。
14)p指向节点I,I没有左节点,p指向I节点的右节点H。
15)p指向节点H,H节点的左节点是I,I右节点指向了H自己,输出节点I,p指向H节点的右节点A。
16)p指向节点A,p左节点最大节点是A,指向了自己,将A节点的右节点指向顺序进行翻转。在翻转过程中,q指向最后一个右节点,R指向了起始节点A,对S指针赋值为H的右节点G,通过这些条件,我们可以从下往上遍历起始的节点左节点的右节点。
输出节点的顺序是H、G、E、D、B,并恢复指针指向状态。p指向A节点的右节点R。
17)p指向节点R,R节点的左节点是A,A右节点指向了R自己,输出节点A。遍历完成。
总结一下:
最主要的是需要理解步骤16,先进行一次翻转,然后输出节点恢复指针状态。
5.3.3 编码实现
// 后序遍历,非递归Morris遍历算法实现
template
void BST::MorrisPostorder()
{
BSTNode* p = new BSTNode(), * tmp, * q, * r, * s;
p->m_left = root;
while (p != 0)
{
if (p->m_left == nullptr)
p = p->m_right;
else
{
tmp = p->m_left;
while (tmp->m_right != nullptr && tmp->m_right != p)
tmp = tmp->m_right;
if (tmp->m_right == nullptr)
{
tmp->m_right = p;
p = p->m_left;
}
else
{
for (q = p->m_left, r = q->m_right, s = r->m_right;
r != p; q = r, r = s, s = s->m_right)
r->m_right = q;
for (s = q->m_right; q != p->m_left;
q->m_right = r, r = q, q = s, s = s->m_right)
visit(q);
visit(p->m_left);
tmp->m_right = nullptr;
p = p->m_right;
}
}
}
}