【算法】学习笔记(三)----Morris前序遍历、中序遍历、后序遍历(C++代码)
Morris遍历
Morris遍历,也称为莫里斯遍历,是一种使用线索二叉树实现的二叉树遍历方法,可以在不使用栈或递归的情况下完成对二叉树的遍历。Morris遍历方法的核心思想是利用每个节点中存储的指向父节点的指针,将左子树中最右侧节点的指向父节点的指针指向当前节点,以便在访问完当前节点的左子树后,能够通过这个指向父节点的指针回到当前节点。这样就不需要额外的空间,实现了空间复杂度O(1)的遍历算法。
Morris前序遍历
morris遍历前序遍历_哔哩哔哩_bilibili
第一步:当前结点的左孩子是否为空,若是则输出当前结点,并更新当前结点为当前结点的右孩子,进入第三步;否则进入第二步。
第二步:在当前结点的左子树中寻找左子树中最右结点作为前驱结点
a.若前驱结点的右孩子为空,则将前驱结点的右孩子指向当前结点,输出当前结点,当前结点更新尾当前结点的左孩子;进入第三步
b.若前驱结点的右孩子不为空(为当前结点),将前驱结点的右孩子置NULL,当前结点更新为当前结点的右孩子,进入第三步
第三步:若当前结点不为空,进入第一步:否则程序结束
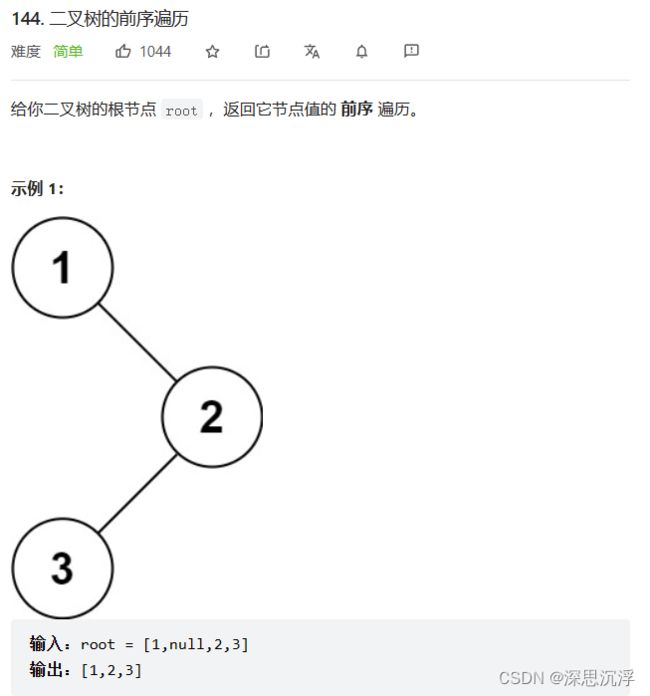
测试题目:144. 二叉树的前序遍历 - 力扣(LeetCode)
采用递归代码:
class Solution {
vector res;
public:
vector preorderTraversal(TreeNode* root)
{
dfs(root);
return res;
}
void dfs(TreeNode* root)
{
if(root == nullptr) return;
res.push_back(root->val);
dfs(root->left);
dfs(root->right);
}
};
时间复杂度:O(n)
空间复杂度:O(n)
Morris前序遍历代码示例:
class Solution {
vector res;
public:
vector preorderTraversal(TreeNode* root)
{
vector res;
TreeNode* curr = root, * pre = nullptr;
while (curr != nullptr) //第三步:若当前结点不为空,进入第一步;否则程序结束
{
if (curr->left == nullptr) //第一步:判断当前结点的左孩子是否为空
{
res.push_back(curr->val); //输出当前结点
curr = curr->right; //更新当前结点为当前结点的右孩子
}
else //第二步
{
pre = GetPreNode(curr); //获取当前结点的左子树中最右结点
if (pre->right == nullptr) //若前驱结点的右孩子为空
{
pre->right = curr; //将前驱结点的右孩子指向当前结点 建立链接
res.push_back(curr->val); //输出当前结点
curr = curr->left; //当前结点更新尾当前结点的左孩子
}
else //b.若前驱结点的右孩子不为空(当前结点)
{
pre->right = nullptr; //还原 去除链接
curr = curr->right;
}
}
}
return res;
}
TreeNode* GetPreNode(TreeNode* curr)
{
TreeNode* node = curr->left;
while (node->right != nullptr && node->right != curr)
{
node = node->right;
}
return node;
}
};
时间复杂度:O(n) 没有左子树的节点只被访问一次,有左子树的节点被访问两次。
空间复杂度:O(1)
Morris中序遍历
morris中序遍历_哔哩哔哩_bilibili
第一步:当前结点的左孩子是否为空,若是则输出当前结点,并更新当前结点为当前结点的右孩子进入第三步;否则进入第二步。
第二步:在当前结点的左子树中寻找左子树中最右结点作为前驱结点
a.若前驱结点的右孩子为空,则将前驱结点的右孩子指向当前结点,当前结点更新为当前结点的左孩子;进入第三步
b.若前驱结点的右孩子不为空(为当前结点),将前驱结点的右孩子置NULL,输出当前结点,当前结点更新为当前结点的右孩子,进入第三步
第三步:若当前结点不为空,进入第一步:否则程序结束
测试题目:94. 二叉树的中序遍历 - 力扣(LeetCode)
采用递归代码:
class Solution {
vector res;
public:
vector inorderTraversal(TreeNode* root)
{
dfs(root);
return res;
}
void dfs(TreeNode* root)
{
if(root == nullptr) return;
dfs(root->left);
res.push_back(root->val);
dfs(root->right);
}
};
时间复杂度:O(n)
空间复杂度:O(n)
Morris中序遍历代码示例:
class Solution {
vector res;
public:
vector inorderTraversal(TreeNode* root)
{
vector res;
TreeNode* curr = root, * pre = nullptr;
while (curr != nullptr) //第三步:若当前结点不为空,进入第一步;否则程序结束
{
if (curr->left == nullptr) //第一步:判断当前结点的左孩子是否为空
{
res.push_back(curr->val); //输出当前结点
curr = curr->right; //更新当前结点为当前结点的右孩子
}
else //第二步
{
pre = GetPreNode(curr); //获取当前结点的左子树中最右结点
if (pre->right == nullptr) //a.若前驱结点的右孩子为空
{
pre->right = curr; //将前驱结点的右孩子指向当前结点 建立链接
curr = curr->left; //当前结点更新尾当前结点的左孩子
}
else //b.若前驱结点的右孩子不为空(当前结点)
{
pre->right = nullptr; //还原 去除链接
res.push_back(curr->val); //输出当前结点
curr = curr->right;
}
}
}
return res;
}
TreeNode* GetPreNode(TreeNode* curr)
{
TreeNode* node = curr->left;
while (node->right != nullptr && node->right != curr)
{
node = node->right;
}
return node;
}
};
时间复杂度:O(n) 没有左子树的节点只被访问一次,有左子树的节点被访问两次。
空间复杂度:O(1)
Morris后序遍历
morris后序遍历_哔哩哔哩_bilibili
新建一个Dummy结点,该结点的左孩子指向树根root,将Dummy作为当前结点;
第一步:当前结点的左孩子是否为空,更新当前结点为当前结点的右孩子,进入第三步;否则进入第二步;
第二步:在当前结点的左子树中寻找左子树中最右结点作为前驱结点:
a.若前驱结点的右孩子为空,则将前驱结点的右孩子指向当前结点,当前结点更新尾当前结点的左孩子,进入第三步;
b.若前驱结点的右孩子不为空(为当前结点),反转当前结点左孩子到前驱结点之间的路径,输出该路径所有结点:再反转恢复原状。将前驱结点的右孩子置NULL,当前结点更新尾当前结点的右孩子,进入第三步;
第三步:若当前结点不为空,进入第一步;否则程序结束;
测试题目:145. 二叉树的后序遍历 - 力扣(LeetCode)
采用递归代码:
class Solution {
vector res;
public:
vector postorderTraversal(TreeNode* root)
{
dfs(root);
return res;
}
void dfs(TreeNode* root)
{
if(root == nullptr) return;
dfs(root->left);
dfs(root->right);
res.push_back(root->val);
}
};
时间复杂度:O(n)
空间复杂度:O(n)
Morris后序遍历代码示例:
class Solution {
vector res;
public:
vector postorderTraversal(TreeNode* root)
{
vector res;
TreeNode* Dummy = new TreeNode();
Dummy->left = root;
TreeNode* curr = Dummy, * pre = nullptr;
while (curr != nullptr) //第三步:若当前结点不为空,进入第一步;否则程序结束
{
if (curr->left == nullptr) //第一步:判断当前结点的左孩子是否为空
{
curr = curr->right; //更新当前结点为当前结点的右孩子
}
else //第二步
{
pre = GetPreNode(curr); //获取当前结点的左子树中最右结点
if (pre->right == nullptr) //a.若前驱结点的右孩子为空
{
pre->right = curr; //将前驱结点的右孩子指向当前结点 建立链接
curr = curr->left; //当前结点更新尾当前结点的左孩子
}
else //b.若前驱结点的右孩子不为空(当前结点)
{
ReverseAdd(res, curr->left, pre); //反转当前结点左孩子到前驱结点之间的路径,输出该路径所有结点,再反转恢复原状
pre->right = nullptr; //还原 去除链接
curr = curr->right; //当前结点更新尾当前结点的右孩子
}
}
}
delete Dummy;
return res;
}
TreeNode* GetPreNode(TreeNode* curr)
{
TreeNode* node = curr->left;
while (node->right != nullptr && node->right != curr)
{
node = node->right;
}
return node;
}
void ReverseAdd(vector& nums, TreeNode* begin, TreeNode* end)
{
if (begin == nullptr || end == nullptr) return;
int pos = nums.size();
while (begin != end) //这里注意不使用do while的原因是最后一次调用ReverseAdd的end->right是Dummy,使用do while会越界
{
nums.push_back(begin->val);
begin = begin->right;
}
nums.push_back(begin->val);
begin = begin->right;
reverse(nums.begin() + pos, nums.end());
}
};
时间复杂度:O(n) 没有左子树的节点只被访问一次,有左子树的节点被访问两次。
空间复杂度:O(1)
练习 Morris逆中序遍历
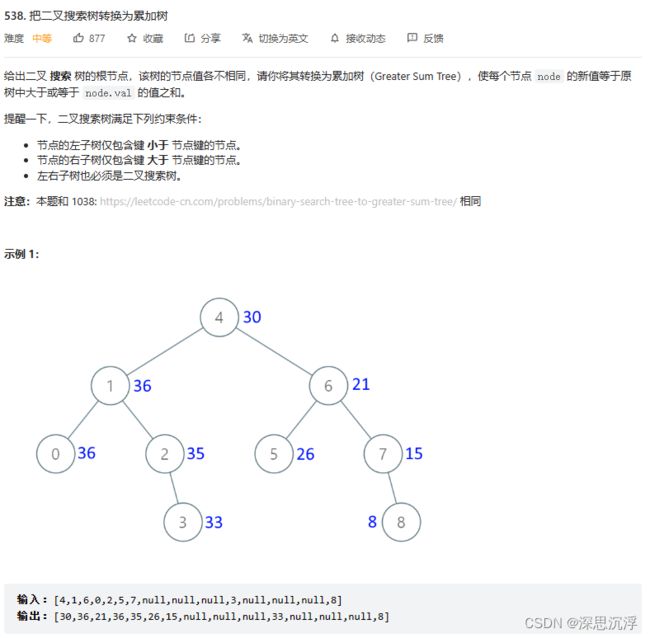
题目链接:538. 把二叉搜索树转换为累加树 - 力扣(LeetCode)
采用递归求解:
class Solution {
public:
int sum = 0;
TreeNode* convertBST(TreeNode* root)
{
if (root != nullptr)
{
convertBST(root->right);
sum += root->val;
root->val = sum;
convertBST(root->left);
}
return root;
}
};
时间复杂度:O(n)
空间复杂度:O(n)
采用Morris逆中序遍历:
class Solution {
public:
TreeNode* convertBST(TreeNode* root)
{
int sum = 0;
TreeNode* curr = root, * pre = nullptr;
while (curr != nullptr)
{
if (curr->right == nullptr)
{
curr->val += sum;
sum = curr->val;
curr = curr->left;
}
else
{
pre = GetPreNode(curr);
if (pre->left == nullptr)
{
pre->left = curr;
curr = curr->right;
}
else
{
pre->left = nullptr;
curr->val += sum;
sum = curr->val;
curr = curr->left;
}
}
}
return root;
}
TreeNode* GetPreNode(TreeNode* curr)
{
TreeNode* node = curr->right;
while (node->left != nullptr && node->left != curr)
{
node = node->left;
}
return node;
}
};
时间复杂度:O(n) 没有左子树的节点只被访问一次,有左子树的节点被访问两次。
空间复杂度:O(1)
总结:Morris逆中序遍历,是吧Morris中序遍历中的所有right替换成left,所有left替换成right,然后根据题目更改输出条件即可。